跳转至

警钟长鸣-题单

那些年, 我做得焦头烂额也(差点)没AC的题.

这是什么

YYDS---永远的伤

2022年6月4日14:00-17:30, 因为笔者算法能力不足, 加之心态不佳, 面对一道背包模板题 "坐牢" 3小时之久, 最后失利收场.

作为一个从大一寒假才开始接触算法的小白, 学习算法和OJ考试之路自然不是顺风顺水, 我虽深受打击, 却反而不愿意直面那些失败, 不敢再反思当时是因为什么原因没有做好. 只是回忆觉得痛苦, 却并没有从中学到什么教训.

我们常说, "learn from failure", 我中考的失败已经告诉我, 失败可以是宝贵的经验, 失败必然说明了不足之处. 因此我创建这个题单, 就是要杀死心中的"畏缩逃避的"自尊心, 鼓励自己大胆地面对曾经那些没有做出来的题, 作一些思考, 作一些尝试.

这个题单会不定期更新(我有时间的时候), 记录一些我做的不太好的OJ题目, 做一些深入的思考.

0x00 2022年转专业机试T3

  • 待更新

0x01 DSOJ(数据结构OJ) W1T3 小蓝鲸排队

  • 题目信息

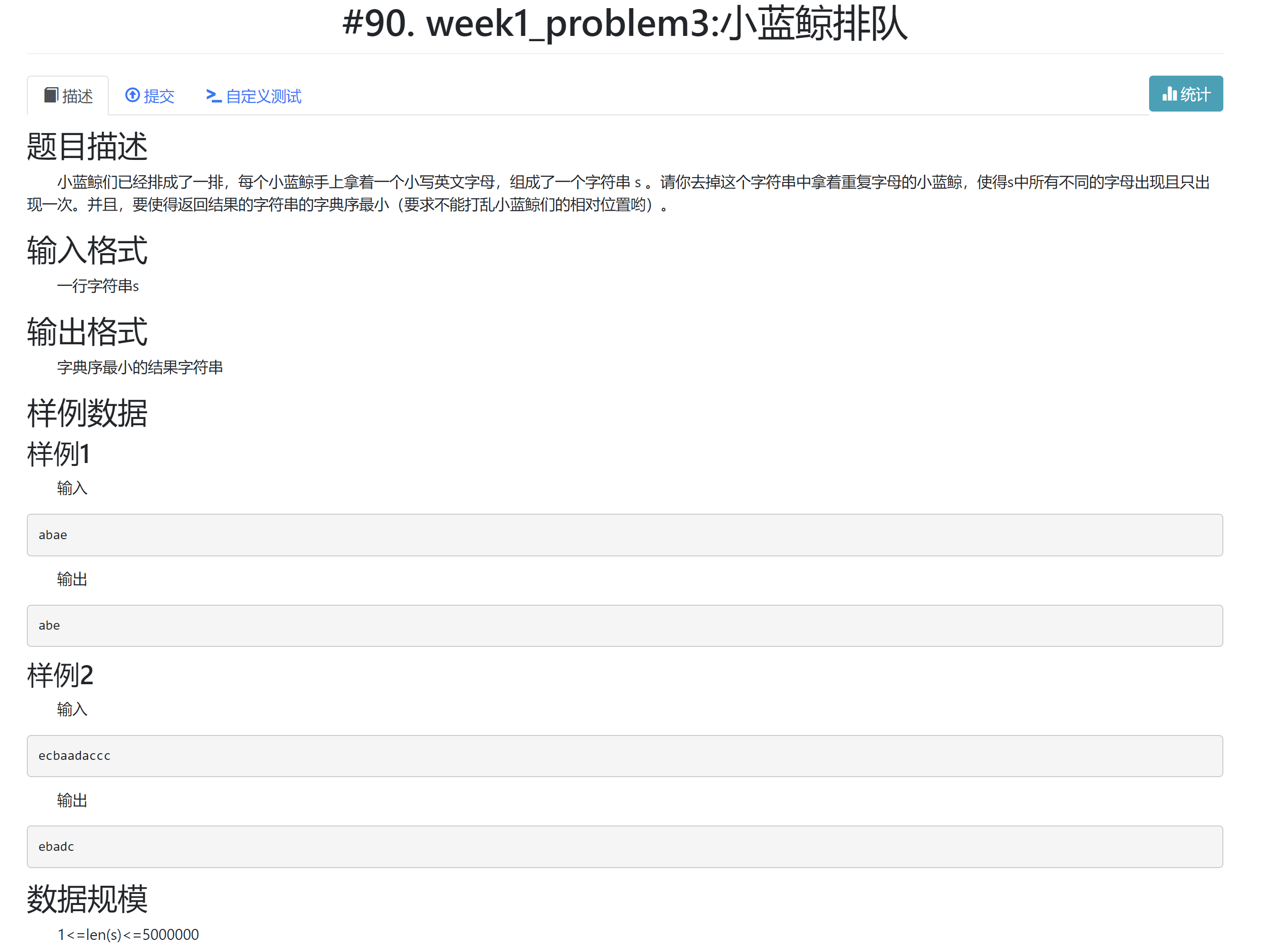
0x01 Info

  • 题目分析:

    • 需要对字母的情况分类:

      • 只出现一次的: 没有选择的余地, 不会被去掉

      • 出现多次的: 只保留一次, 使得最后剩下的字符串字典序最小

        反思: 怎么样会使得字典序最小? 没有分析清楚

    • 贪心问题: 因为最后的答案是确定的, 且每一位都应该选择字典序最小的字母.因此问题可以拆分成至多26个循环, 每次都确定并往最终的答案里填充一个字母.

    • 从数据规模分析: 更可能的情况是26个字母都会出现, 因此其实就是对26个字母定序.

      显然, 最小的排序是"abcd...xyz", 这里面每一个字母的最小排序位置也就是1,2,3...,26.

笔者第一遍思路

迭代26个循环, str从左到右, 每次确定一位字母.

在一次寻找的过程中, 从startIdx开始, 逐一判定之后的出现次数,

  • 如果!=1, 说明 可以不选 这个人, 继续向右比较, 每次只记录字母最小的那个人的位置(注意: 如果这个字母多次出现的话, 要记录第一次的, 否则会去掉一些情况, 我一开始就是这块没想清楚)

  • 如果==1, 说明这个字母就只剩他一个人了, 因此必须保留, 于是比较到这里终止.(因此在这个人之前, 可能包括他自己, 必定需要选一个人出来, 如果选不出, 那就是这个人了). 返回字典序最小的字母 第一次出现 的位置.

  • 第二种终止的情况: curIdx越界, 说明 没有一个人只出现一次, 因此就返回字典序最小的字母 第一次出现 的位置.

源码: 虽然AC, 但是仍然觉得写的混乱

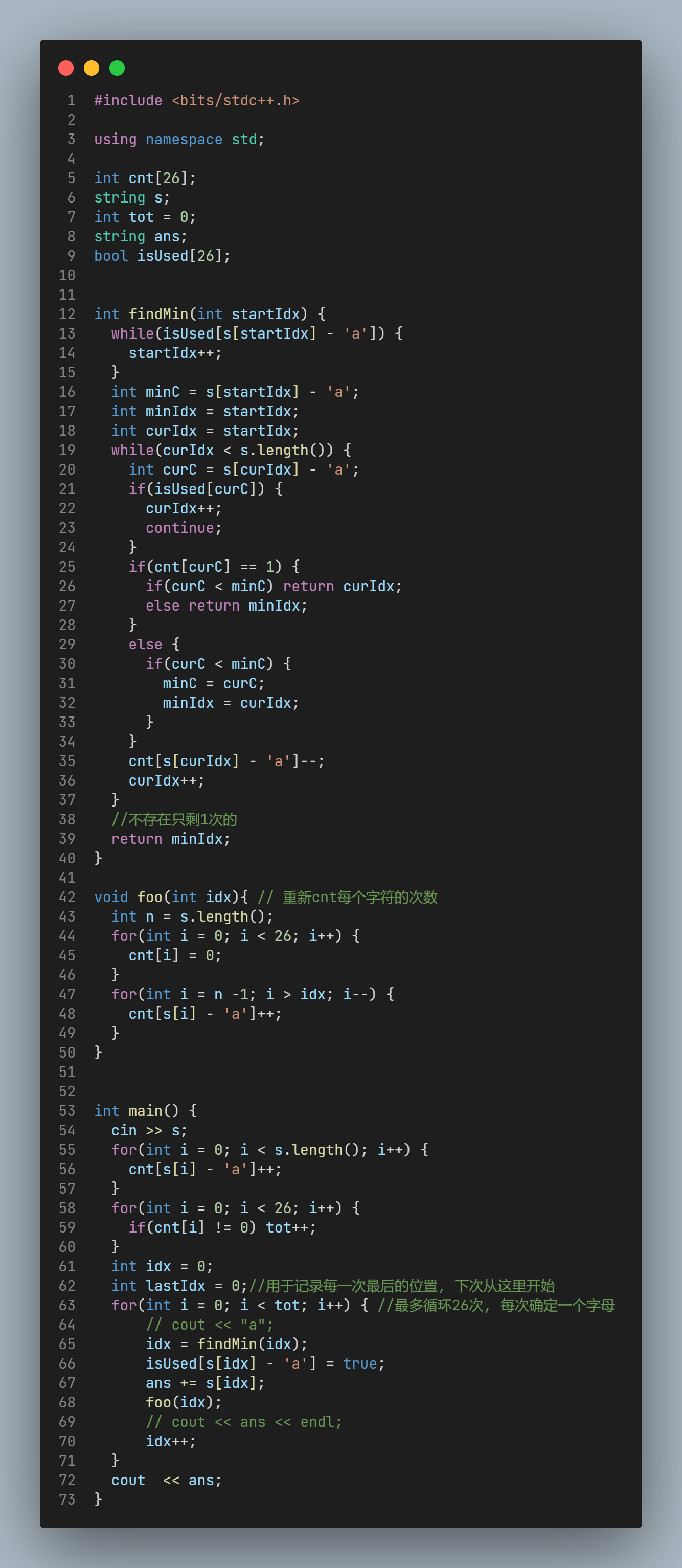
0x01 SrcCode

暴露的问题

一个小问题, 100分变0分!!!

Summary

  • 想清楚, 尤其是出现了问题(哪怕是0分), 因为0分和100分, 也许只差一个"="号!

  • 出现问题的时候, 不要胡乱尝试, 打乱节奏, 一定是问题没想清楚! 找一个例子, 再手推一遍, 理理思路.

0x02 DSOJ(数据结构OJ) W2T1 小蓝鲸学数组

  • 题目信息

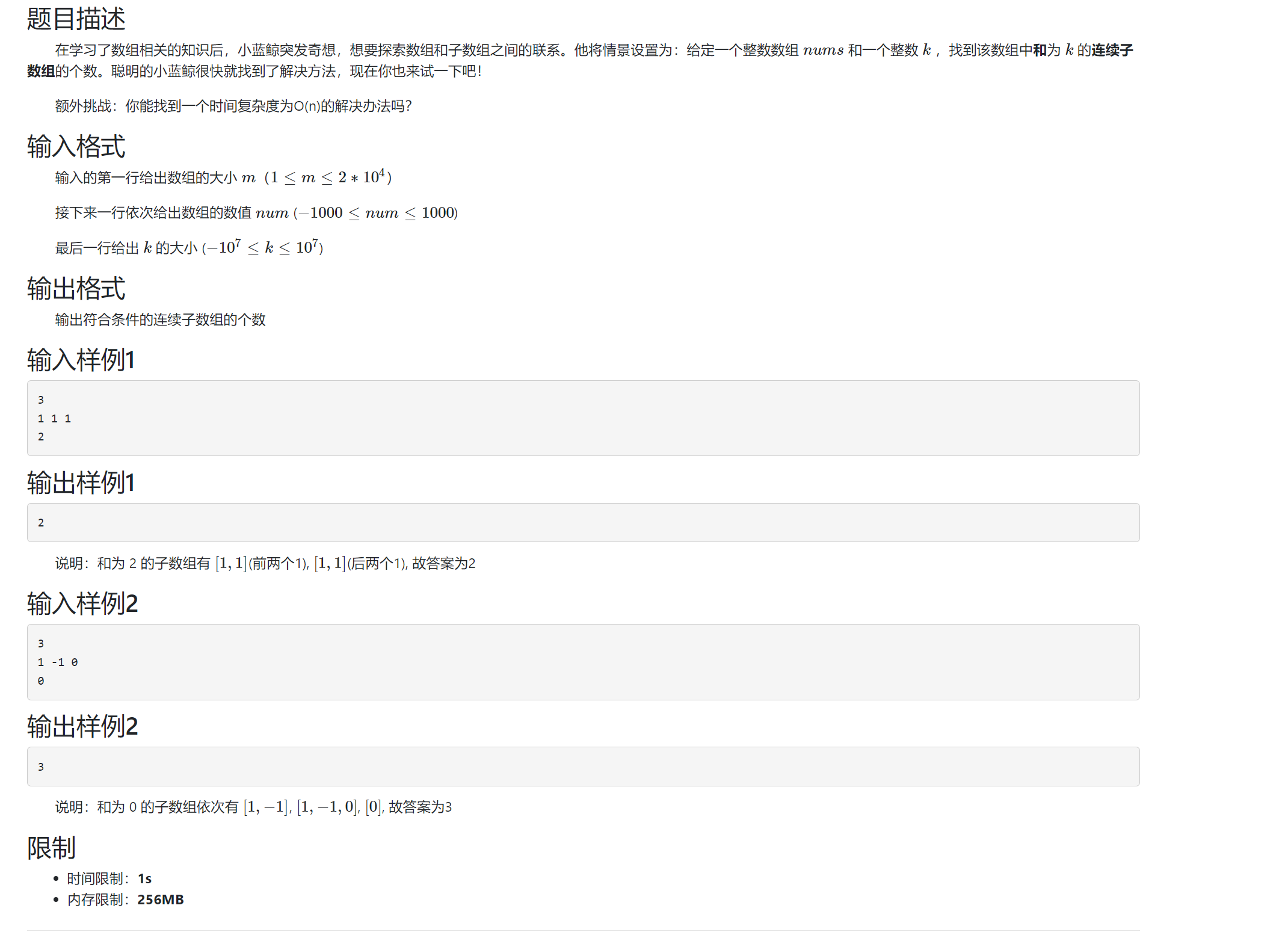
  • 题目分析

  • 连续数组->自由度为2:起点&终点->最坏的时间复杂度:O(N^2)(遍历所有的起点和终点可能即可)

  • 难点在于如何实现O(N)算法. 看一眼数据范围, 发现有好消息: 数组的值很小(-10^3\le val\le 10^3), 而连续子数组的总和2\times 10^7\le sum\le 2 \times 10^7, 这个值其实不算大! 这就启发我们, 要充分利用空间, 以空间换时间.

笔者思路

前缀和+cnt数组. 不难发现这个连续子数组有两个变量:起点和终点, 看起来是两端都在浮动. 如果能想到前缀和,就能解决这个问题.

记输入的要求子数组和为targetVal, 从左向右迭代的指针为curIdx,对应的前缀和为curSum,记curIdx前另有一段终点为prevIdx的连续子数组(注意 prevIdx != curIdx 否则两段数组相减就没有剩余的连续子数组了), 其对应的前缀和为prevSum.

将连续子数组的和转化为两段起点为0, 终点为curIdx与prevIdx的连续子数组之差. 这样的数组只要知道终点, 就能知道对应的值.

看起来, 我们并不知道prevIdx,但是, 我们知道期望的prevIdx对应的子数组和应该为curSum - targetVal, 因此, 我们并不需要知道具体的前一段子数组在哪里, 只需要知道有几个符合这样的子数组即可. 因此使用cnt数组来记录之前的子数组数目.

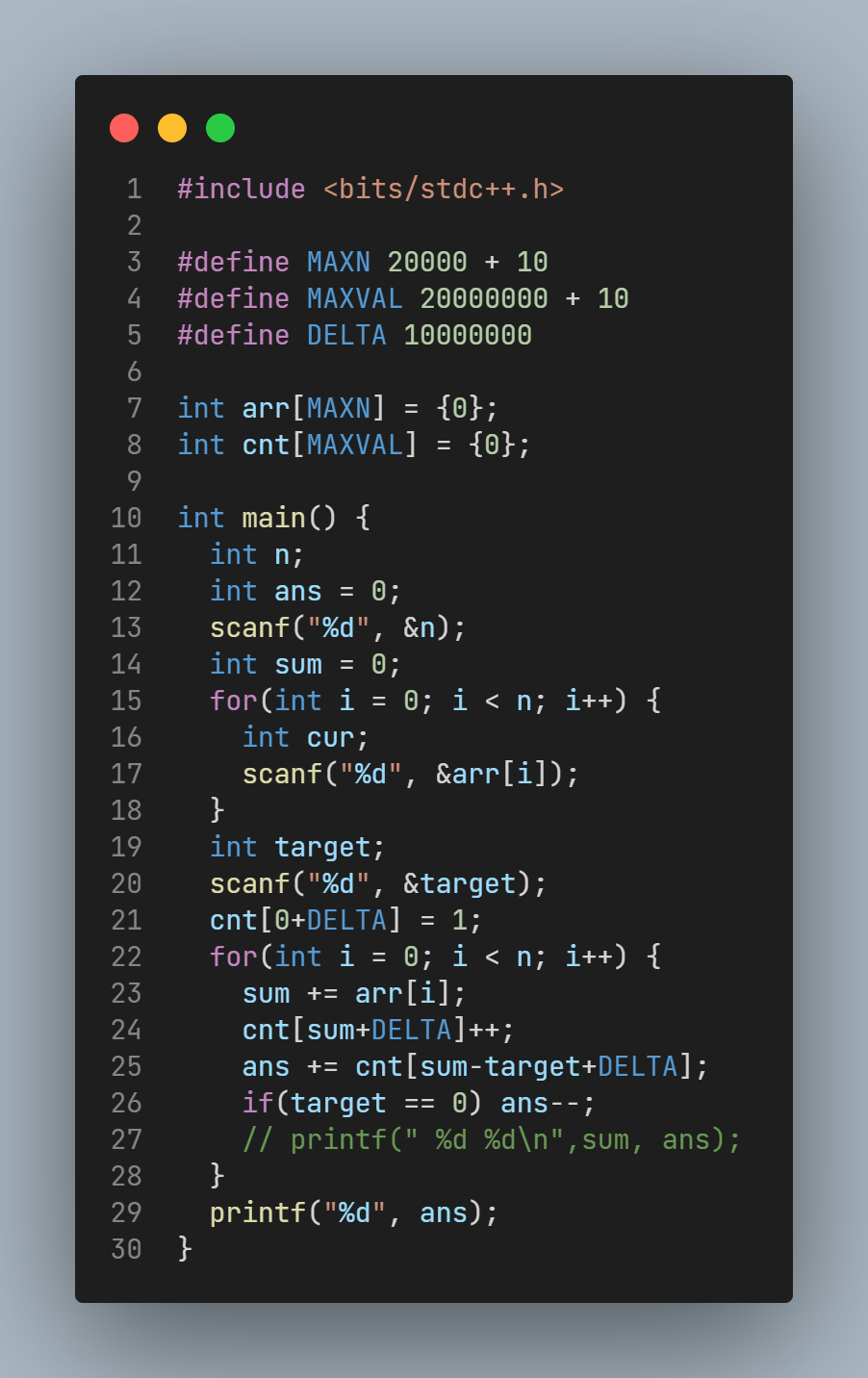
从左向右迭代一次curIdx, 每次ans += cnt[curSum - targetVal]即可.

Ps: 由于此题前缀和可能为负, 而数组下标不能, 因此需要添加一个偏置常数.

O(N)

0x02 SrcCode

0x03 LGOJ P1160 队列安排

  • 题目信息

数据范围

对于20%的数据，有 1\leq N\leq 10

对于40%的数据，有 1\leq N\leq 1000

对于100%的数据，有 1\leq N,M\leq100000。

  • 题目分析

简单的数据结构题, 就是构造一个双向链表, 但是问题在于数据范围较大, 而链表的访问效率是很低的, 而这题要求随机读取, 因此需要一些别的技巧: 把插入的每个门牌号记下来.

一般, 内存限制128MB的话int型数组可以开到10^7级别, 因此这题已经够用.

AC

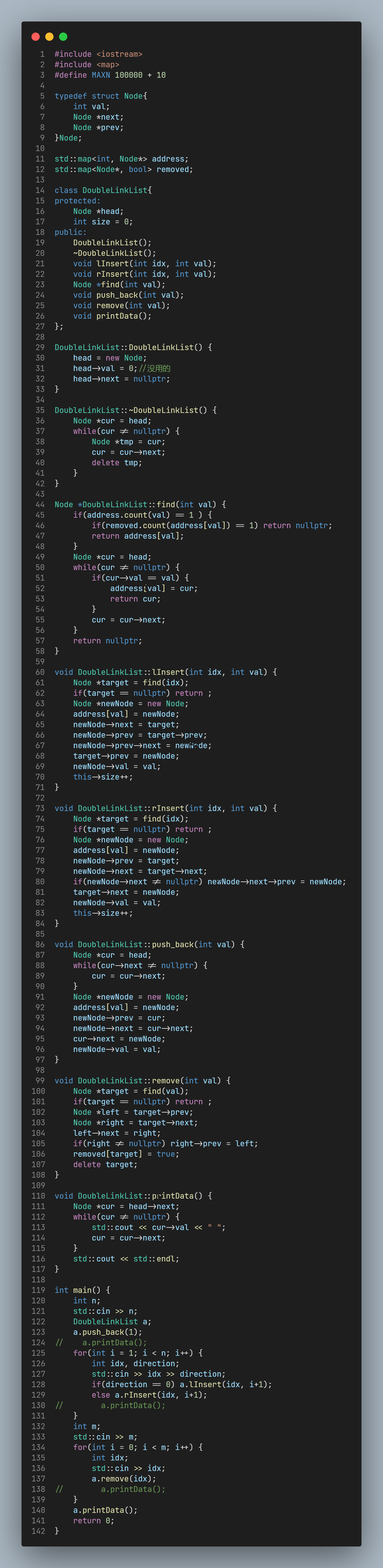
review

介于本题需要查找的值是连续的, 且就是同学的序号, 因此更好的解决办法是用数组模拟双向链表

[TODO]

0x04 DSOJ W3T3 小蓝鲸乘法

  • 题目信息

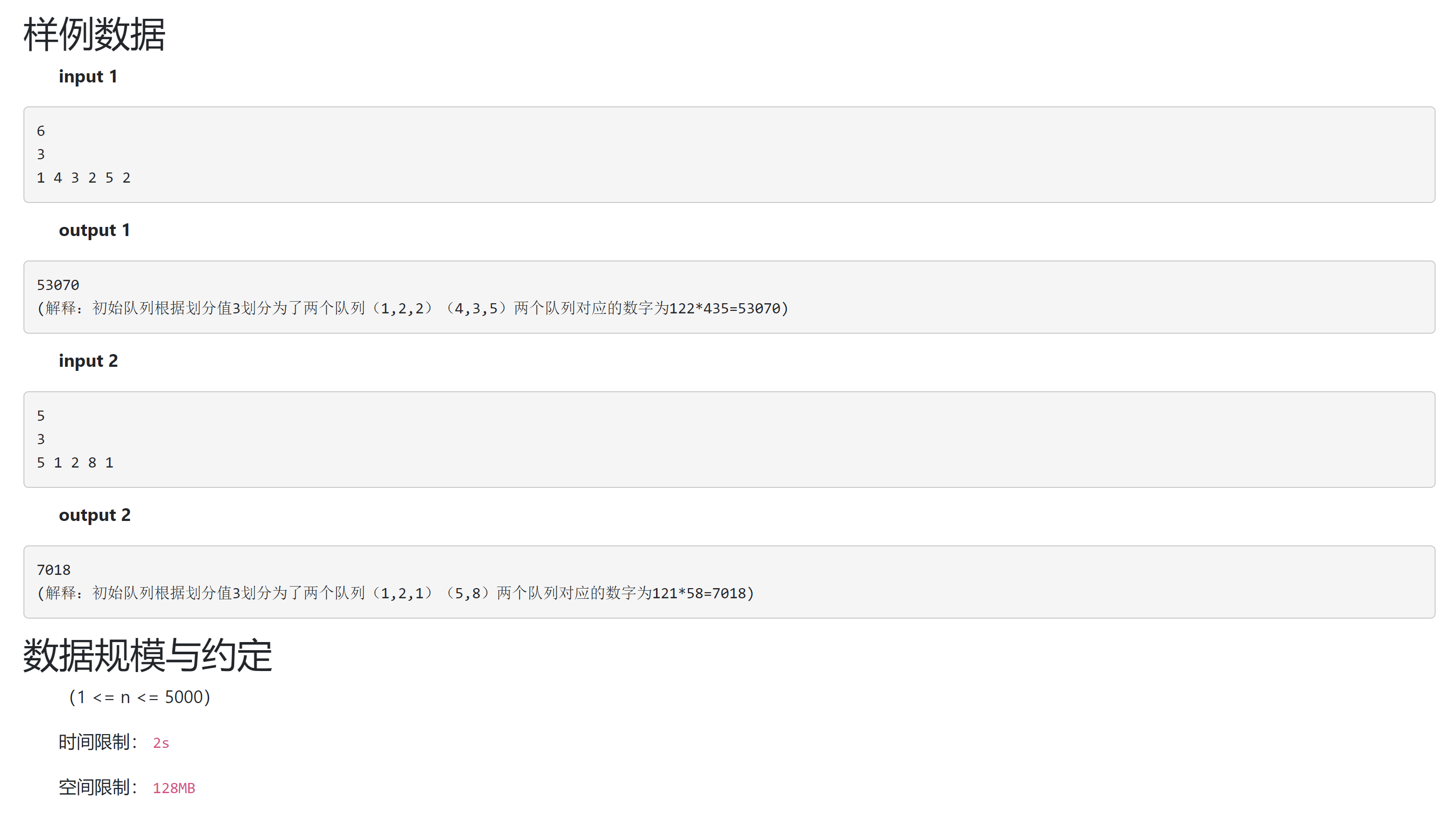
  • 题目分析

高精度乘法的裸题. 但是有一些细节需要强调:

  • 边界情况: A \times B, 而A/B == 0.

  • 前缀0: 例如01\times 22 = 22, 需要去除两个乘数的前缀0

  • 开辟空间需要及时释放, 否则MLE.

关于内存释放的问题

ans = this->plus(ans, newAns);
this->deleteNode(newAns);
这两行代码看起来完成了释放, 但是并没有释放完全, 因为this->plus(ans, newAns)返回的是新的地址, 然而原先的ans指向的内存并未释放!!!

教训

多注意new和free的匹配. 尤其是MLE的时候.

AC

0x05 栈输出的合法序列

  • 题目信息

题目源头是数据结构课上的一个小问题: 给定栈的输入序列, 求所有栈的合法输出序列.

  • 题目分析

意思就是说, 虽然给定了入栈序列, 但是由于入栈/出栈的操作是交织进行的, 对于同个栈的状态, 可以有入栈/出栈两种合法的操作, 因此就对应了两条不同的输出路径.

简单画图发现, 所有的情形对应了一棵二叉树, 寻找所有合法序列事实上就是对二叉树进行遍历的过程. 因此可以简单写一个DFS进行递归.

具体来说, 先定义, 什么是一个状态: 当前的栈内信息stk+还有哪些元素未入栈(即指向已经入栈的元素的指针curIdx), 因此, 状态的转移:

  • 对于入栈操作(前提是不能栈上溢): stk.push, curIdx++;

  • 对于出栈操作(前提是不能栈下溢): stk.pop, 同时记录出栈元素

递归的终点就是当确定所有的元素全部入栈时.

AC代码如下

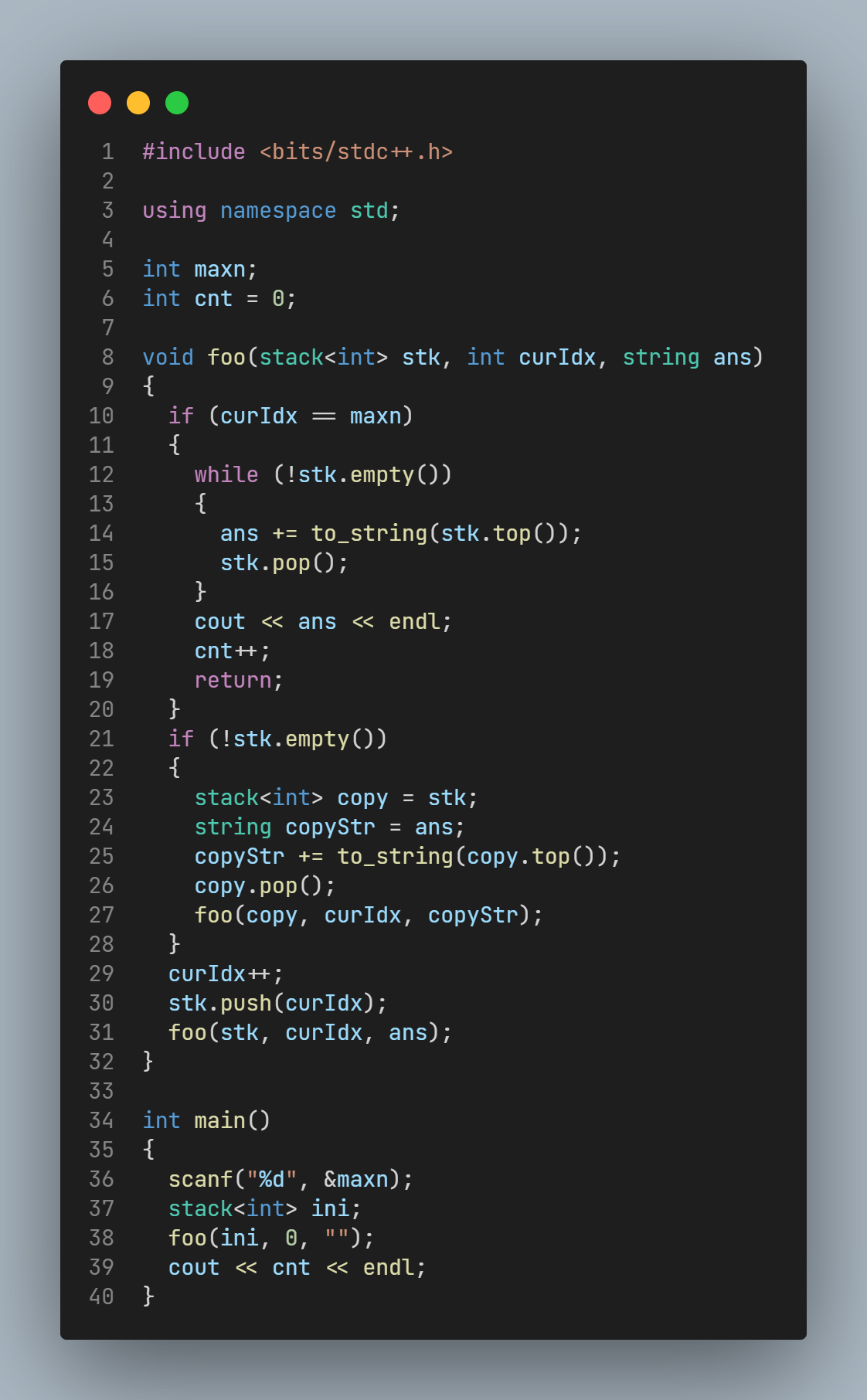
进一步思考

题目虽然写出来了, 但是对栈的思考其实未必到位. 不难问出以下几个深入的问题:

  • 对于入栈序列1,2,\cdots, n, 出栈序列的种数cnt关于n的关系式是什么?

  • 如何判断一个序列是否是合法的出栈序列?

一些思考

f(n) = \sum _{i = 0}^{n-1}f(i)\cdot f(n-1-i)

因此, 算法的复杂度为O(1 + 2 + 3 + \cdots + n) = O(n2).

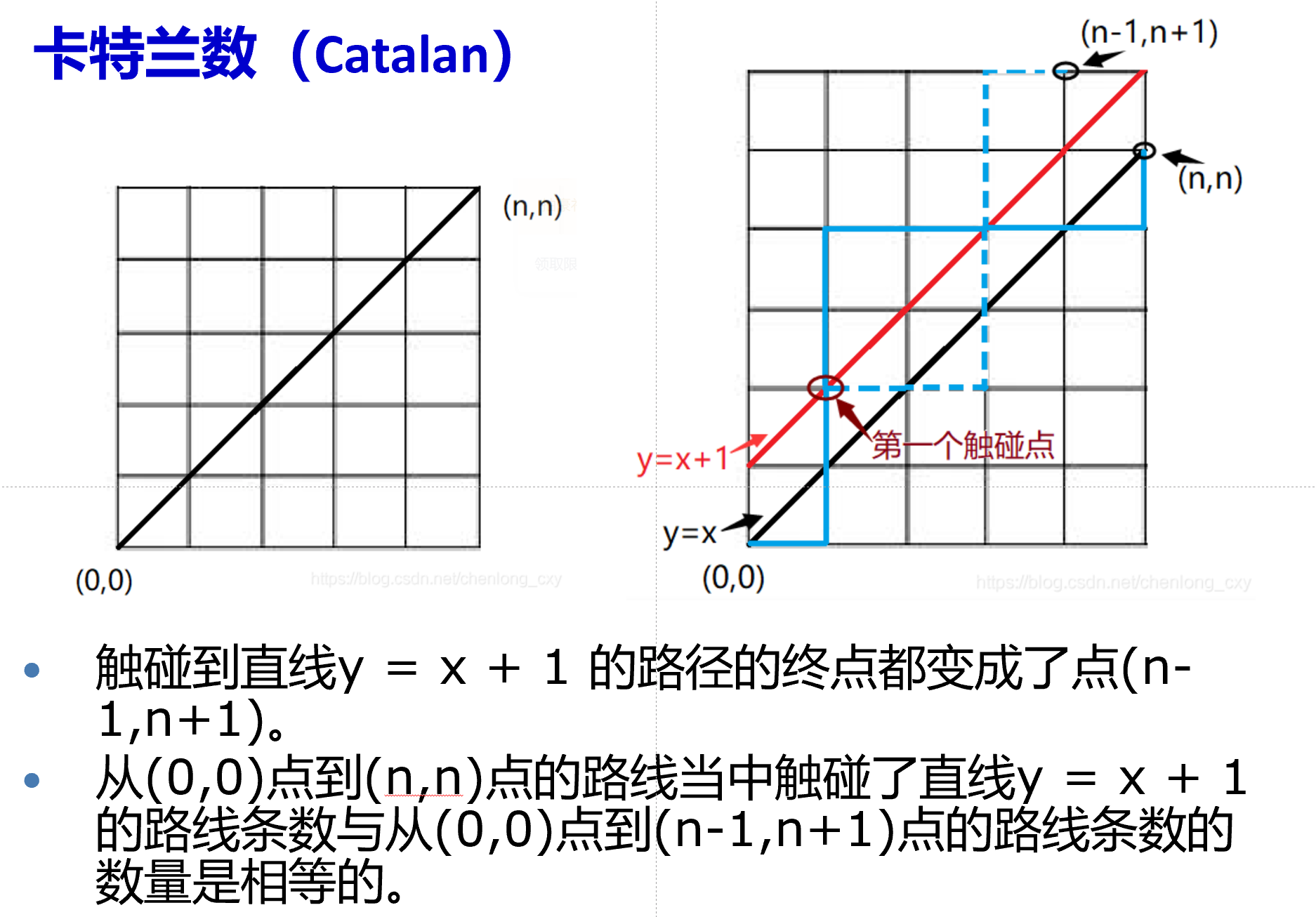
引申: 卡特兰数

f(n) = C_{2n}^n - C_{2n}^{n-1}

0x06 [0x05]的延伸 出栈序列

  • 题目信息

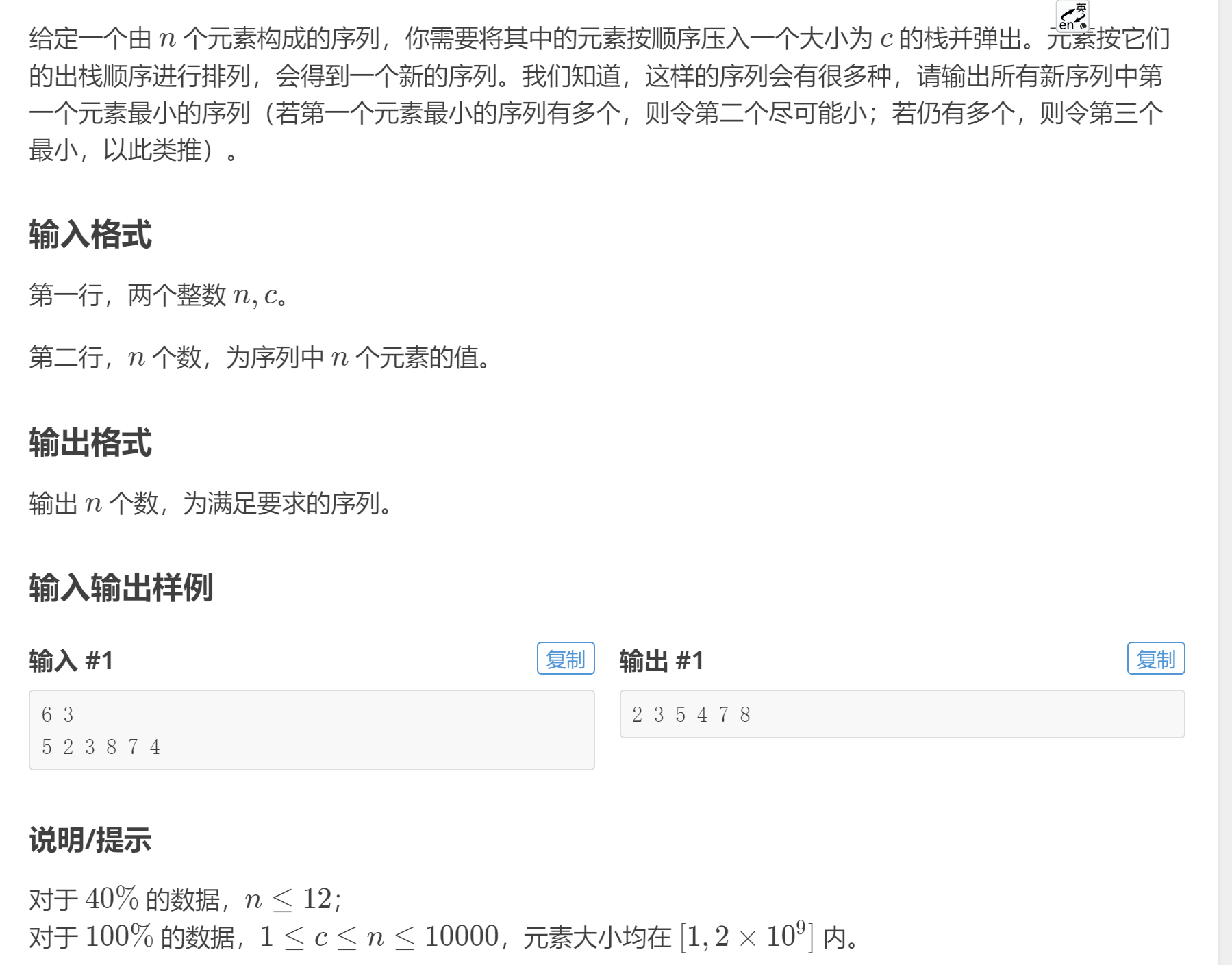
  • 题目分析

[TODO] LeetCode第328场周赛T4 最大价值和最小价值和的差值

  • 题目分析

首先注意到题目数据中price[i] >= 1, 这个条件大大简化了题目的要求, 因为对于任何节点开始的最小价值路径, 必然就是当前的根节点, 而再增加任意节点都会使路径和增加, 这样的话, 最大价值路径-最小价值路径=当前节点的所有子节点为起点的、不经过当前节点的最大价值路径。

之所以要强调**不能经过当前节点**, 是为了避免搜索的过程中发生重复遍历, 即a->b->a这种情况, 也就是要求不能访问已经访问过的节点. 这里可以通过一个vis[]数组来保存已经访问过的节点, 也可以利用树的性质: 树中一条路径上, 当前节点除了与其父节点直接相连, 不会与其任何祖先相连, 否则就会出现环. 这样一来, 我们只需要在dfs的时候记录当前节点的父节点, 避免重复访问父节点即可.

  • 解题思路

现在, 我们先不考虑数据规模, 看看如何求解对于一个特定顶点为根的最大开销. 根据之前的分析, 也就是求解**根节点所连子节点的最大路径的最大值(不能经过根节点). 然后, 就会发现这里存在一个关系的递推: 根节点所连子节点为起点的最大路径值=这个子节点的price+该子节点的子节点的最大路径值.我们发现这个递归关系的两个量都是只关于当前节点的值, 也就是说, 可以通过记忆化**每个节点的所有子节点为起点的最大路径值, 来避免重复计算. 当完成了所有的记忆化工作后, 取之中的最大值, 就是答案.

定义函数int dfs(int cur, int fa), 该函数求解并返回以当前节点为起点的且不经过其父亲节点的路径中的最大值, 不难发现每一次这样的函数访问就对应了图中的一条有向边.

最后, 我们注意到, 由于在单次dfs的过程中不允许重复访问, 这导致对于每一个访问到的子节点, 是不会求解以其父节点为起点的最大路径值的, 这就导致单次dfs并不能完成全部的记忆化. 不过好在记忆化避免了重复计算, 每一条边对应的dfs(cur, fa)只会访问一次, 因此不妨对每个顶点做一次dfs(cur, -1), 并在过程中更新最大值, 最后返回即可.

  • 复杂度分析

    • 建立邻接表的复杂度为O(V) = O(N),

    • 由于记忆化的原因, dfs只会被调用O(V) = O(N)次.

因此总体的时间复杂度为O(N).

空间复杂度为O(N).

  • 代码
class Solution {
  vector<vector<long long int>> v;//每一个顶点以某个点为起点的最大路径和
  vector<vector<int>> adj;//邻接表
  vector<int> price;
  long long ans = 0;
  long long int dfs(int cur, int fa) {
    //得到该点下面的所有节点的路径和
    long long int ret = 0;
    for(int i = 0; i < adj[cur].size(); i++) {
      int to = adj[cur][i];
      if(v[cur][i] == 0 && to != fa) {
        v[cur][i] = dfs(to, cur);
      }
      if(to != fa && v[cur][i] > ret) ret = v[cur][i];
      if(v[cur][i] > ans) ans = v[cur][i]; 
    }
    return ret + price[cur];
  }
public:
    long long maxOutput(int n, vector<vector<int>>& edges, vector<int>& price) {
      adj.resize(n);
      v.resize(n);
      this->price = price;
      for(auto edge : edges) {
        int u = edge[0];
        int v = edge[1];
        adj[u].push_back(v);
        adj[v].push_back(u);
      }
      for(int i = 0; i < n; i++) {
        v[i].assign(adj[i].size(), 0);
      }
      for(int i = 0; i < n; i++) {
        dfs(i, -1);
      }
      return ans;
    } 
};

初步分析: 直接模拟的话显然超时.

0x06 DSOJ W3T2 小蓝鲸排队3

  • 题目信息

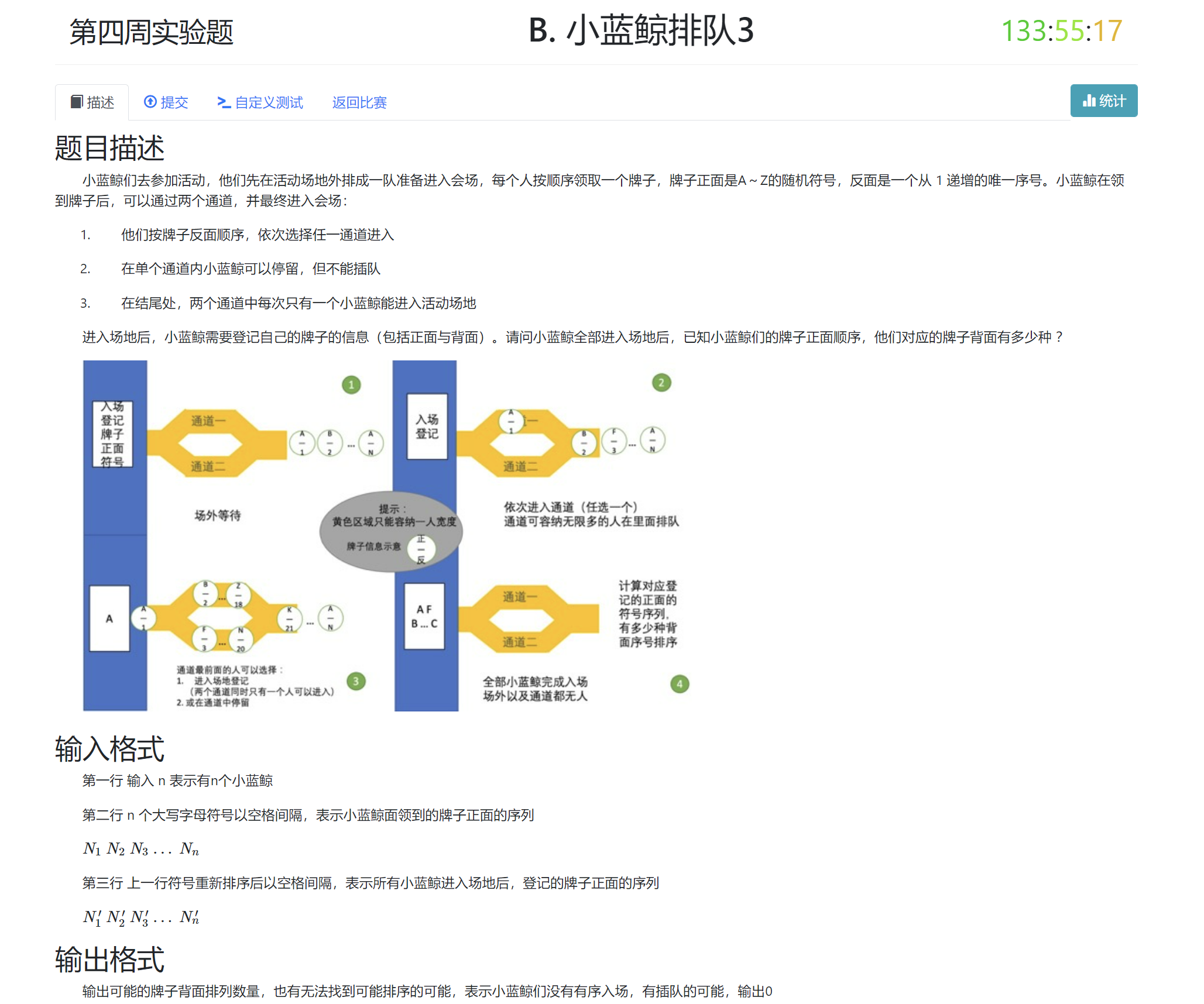
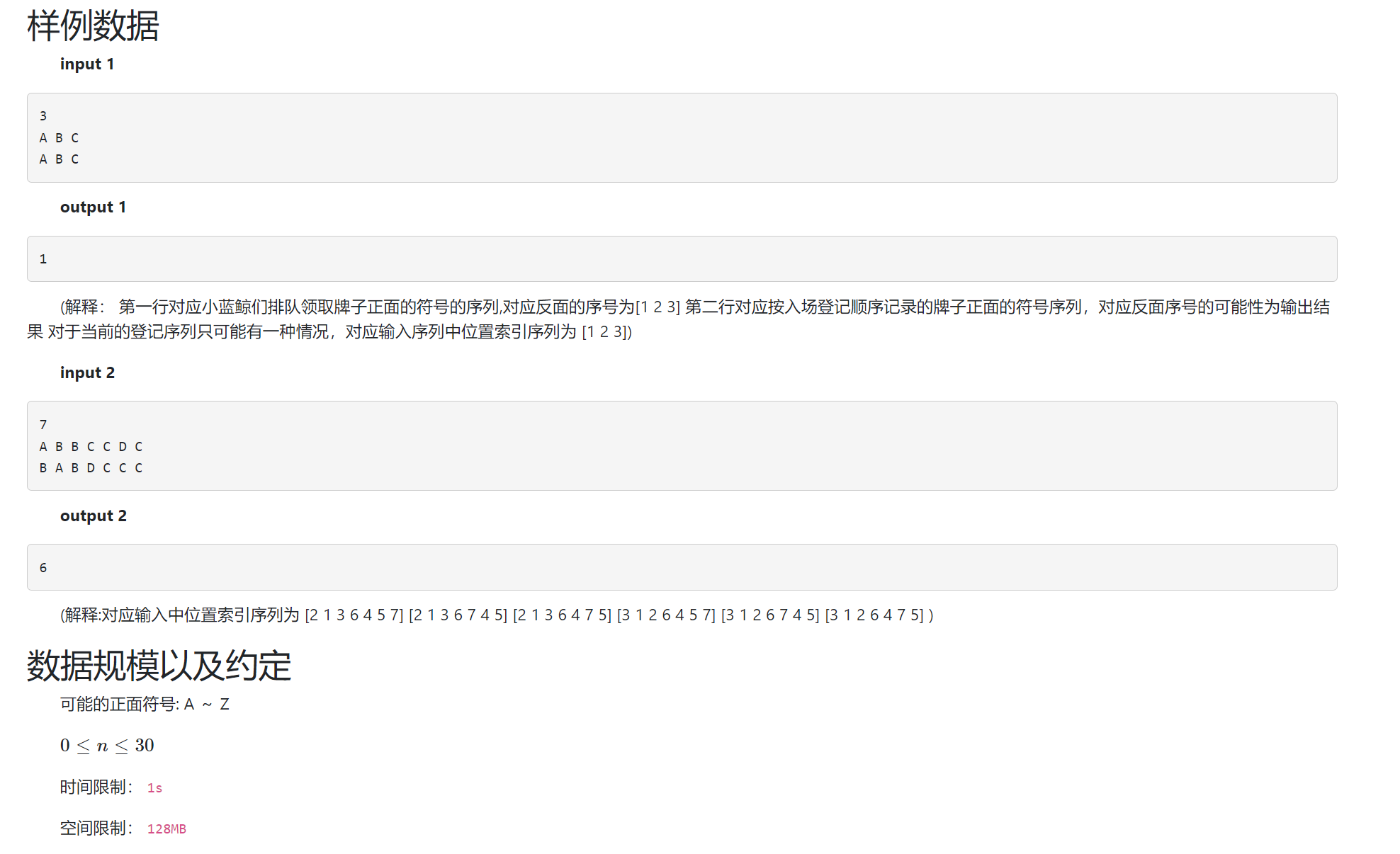
  • 题目分析

思考: 为什么会导致对应的可能序列有多种?

显然, 原因在于同一个字母可能存在多个"小蓝鲸", 举例来说C \cdots C C \cdots, 这3个C就有A_3^3 = 3!种排列方式, 但是, 进一步思考: 这3!种序列都是合法的吗? 这就需要结合题目的 双队列要求 进行合法性判定, 显然, 容易举出不合法的例子(如样例).

这样看来, 似乎该题的要点之一就是 如何判定给定的一个序列是否是合法的序列 .

由于题目规则, 每一个"小蓝鲸"选择队列是任意的, 同时两个队列每次通过的一个"小蓝鲸"也是任意的. 这就导致 存在多种排队方法, 最终得到相同的序列. 然而, 题目只需要我们输出所有的合法的序列, 因此我们不用管 一个结果序列是具体通过什么排队方式得到的 , 只需要构造一种排队方式使得这个结果是合法的即可. 这是通过结果反推(构造)过程来判定结果合法性的方法.

下面, 来思考这个合法性判定函数怎么写.

首先, 需要观察到, 对于结果的合法性, 我们只需要关注小蓝鲸的序号, 而小蓝鲸的分组(ABCD...)是不影响结果合法性的判定的.因为在排队的过程中, 不会因为属于不同的字母, 对排队的规则产生任何分歧. 我们只是要求序号小的先入队列.

既然通过结果反推, 我们逆向思考, 从结果序列入手, 通过依次给结果序列中的每一个序号分配通道, 把小蓝鲸"塞回队列", 然后需要满足小蓝鲸从队列中退出, 最后得到原始的[1 2 3 ...]序列.

然后, 通过样例来举例说明.

构造过程

首先, 不失一般性, 2进入队列1;

由于2先出队, 因此1只能进入队列2, 否则, 就会导致1先于2出队, 这就意味着2先于1入队.

对于3, 这时候就发现, 3可以任意进入队列1或者队列2 , 对结果没有任何影响, 这一点先记住, 我们假设3进入队列1

对于6, 同3, 不失一般性, 我们假设6进入队列1;

这时候, 我们发现, 4不能安排到队列1中了, 因为这样的话相当于6比4先入队, 因此只能将4安排到队列2;

同理, 5->队列2;

对于7, 同3, 不失一般性, 安排到1;

完成还原构造, 得到如下图所示的队列情况, 不难说明可以还原回入队时的[1 2 3 4 ...], 因此合法.

下面来看一个不合法的例子:

[2 1 3 6 7 5 4]

如上方法, 安排到4的时候发现: 无论如何安排, 两个队列的最后一个元素均大于4, 因此4无法入队. 因为两个队的最后一个元素都比4大, 如果4入队, 就说明4晚于这些元素进入队列, 这显然是不对的.

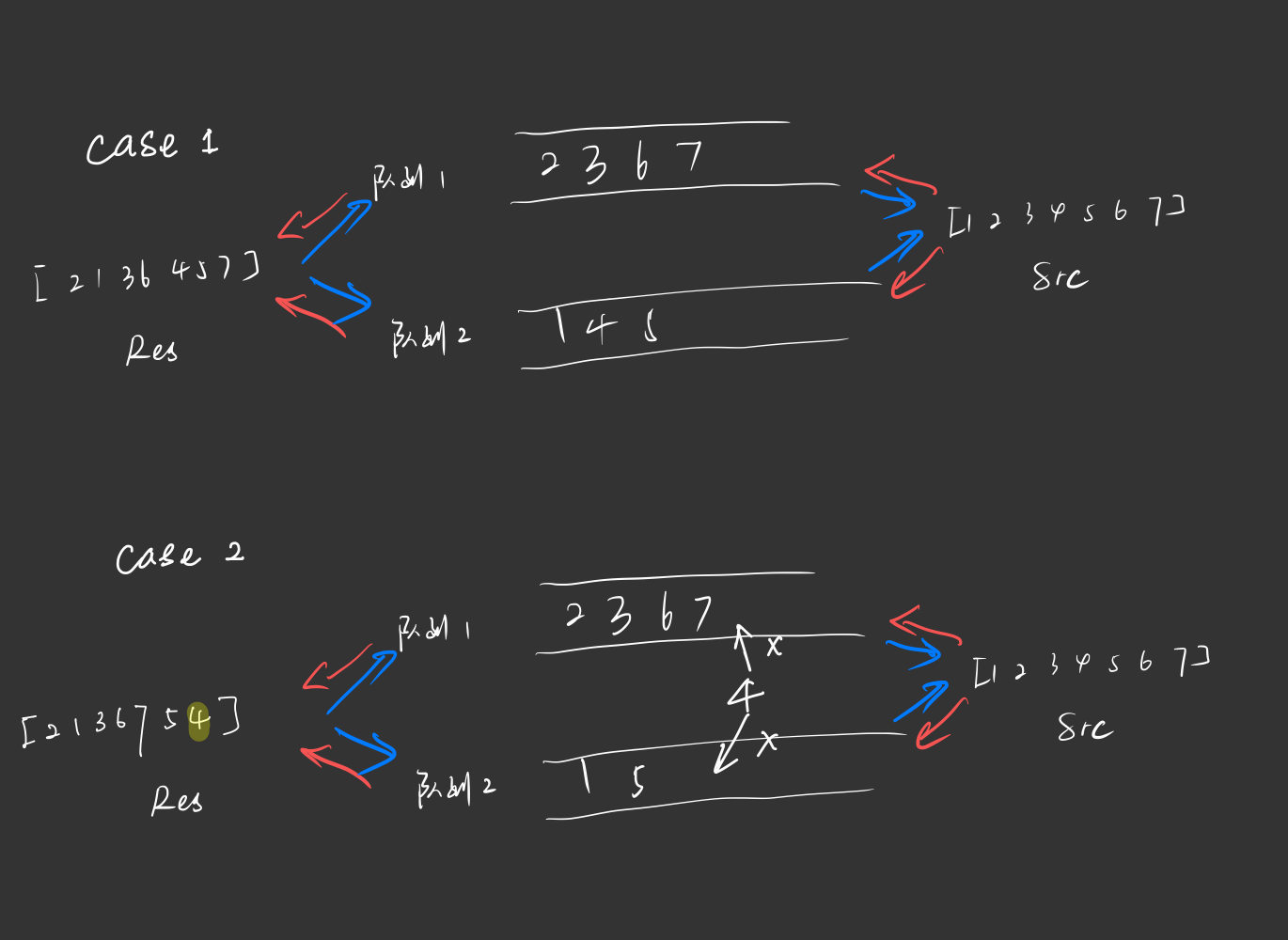
至此, 我们可以归纳不合法的判据:

  • 两个队列满足单调增的性质, 即, 每次入队的元素需要大于当前的队尾的元素. 这反映在题目中就是序号小的先入队.

  • 因此, 对于一个结果序列, 如果无论如何构造, 都存在一个元素无法入队时, 就说明这个结果是不成立的.

  • 那么, 怎么证明 无论如何也不能呢? 这里就要用到之前发现的一个性质: 当入队的元素均大于两个队列的队尾元素时, 可以进入任意队列. 不难发现, 这里存在最优解的情况, 即, 每次都选择当前队尾元素较大的队列入队, 这样更有可能满足两个队列的递增性质, 因此如果这样的策略也不满足, 则说明其余构造也不能满足.

至此, 我们解决了如何判定合法性的问题. 下一个要点是, 怎么生成所有的待判定的序列呢?

不难想到, 不就是全排列么, 不过这部分的代码还是很考验码力的, 因为是一个复合的全排列, 实现起来不简单.

大体的思路就是全排列的思路: dfs + 回溯.

构造序列方法

首先, 明确排列分配过程: 对于同类字母的结果序列, 分配原始序列中的idx. 因此首先做一下数据处理, 这部分略.

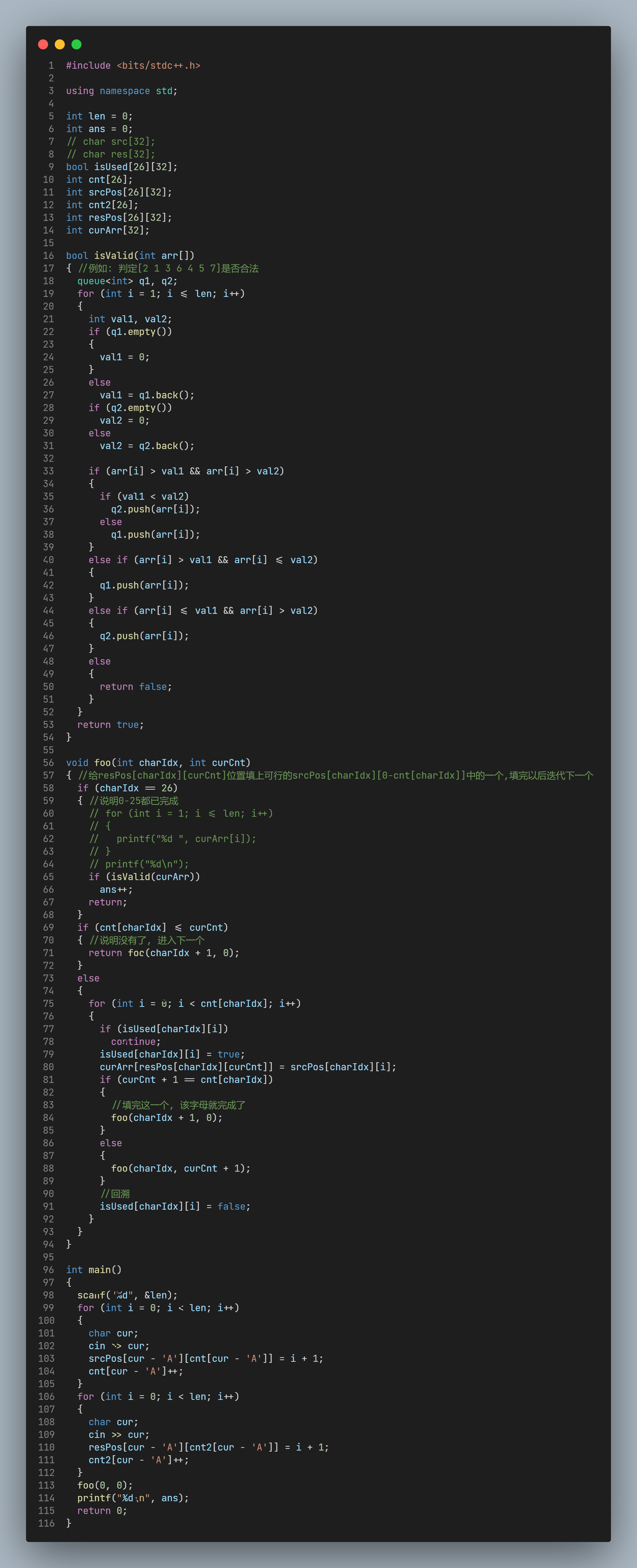
然后, 就是往结果序列(一开始是空的)中填入idx的过程了. 写一个foo(int charIdx, int curCnt)函数, charIdx表示当前处理的字母, curCnt表示正在尝试填入的是结果序列中第curCnt个该字母对应的位置.

从A-Z遍历, 每个字母又是从第1个知道全部填完, 回溯法就需要有记忆数组int isUsed. 每次选择一个未被使用的原始idx, 递归填写下一个, 返回的时候还原该idx的使用状态.

递归的重点就是Z字母的最后一个位置被填完. 这样就得到了一个完整的结果序列, 带入之前写的判定函数即可.

dfs爆搜

0x07 DSOJ W3T3 小蓝鲸找矩形

  • 题目信息

  • 题目分析

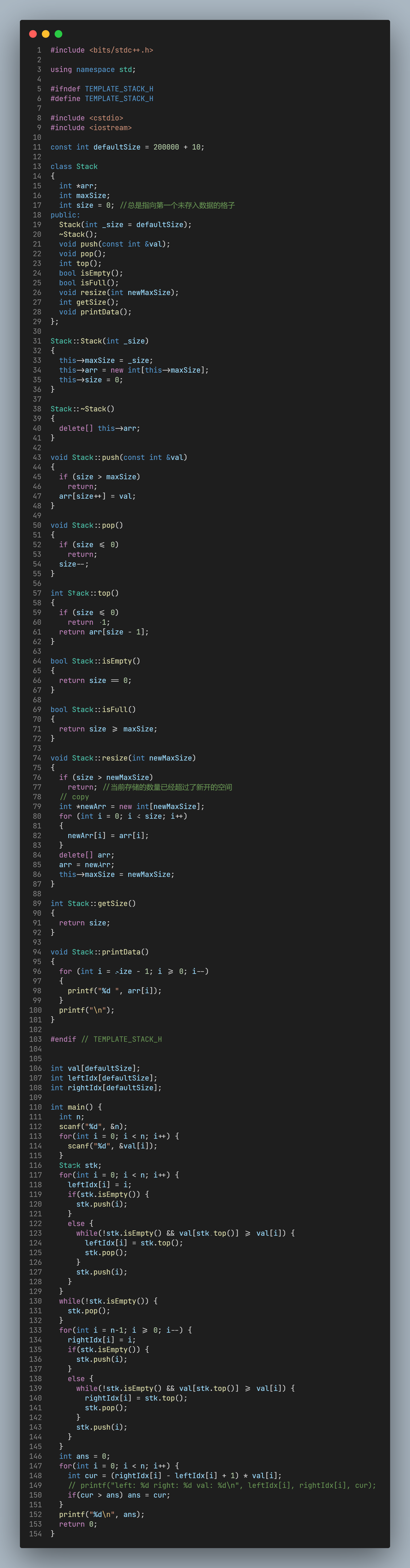
所有的可能矩形有三个自由度: 左端位置 右端位置 矩形高度 单调栈的想法是: 从左到右遍历每一个柱子, 以其高度为矩形高度, 然后尽可能向左和向右延展(直到左/右出现柱子高度比当前这个高度低) 那么以该柱子为矩形高度的最大矩形就=(rightIdx - leftIdx + 1) * height[curIdx]

所以目标就是以O(N)的复杂度来找到每一个柱子左边有几个大于等于它的, 右边有几个大于等于它的.

为什么想到单调栈?

比起怎么利用单调栈完成这道题, 更难的是: 怎么自然的想到使用单调栈?

单调栈 O(N)

0x08 APOJ(高程OJ) W3 又是指针的坑

题目理解很重要

对于设计类型的题目, 很大的难点在于 完全正确理解题目意思 , 否则很可能基于一些习惯进行设计, 结果带来的错误就几乎不可能改出来了, 因为你根本就不会想到存在这样的问题.

例如, 本题中通过传递指针来进行careerTalk变量的传递. 潜意识里告诉我, 如果直接使用传入的指针, 而不是创建一个类并进行拷贝的话, 可能会出现很大的问题(然而本题中其实并不会, 还是没有想清楚), 例如指针指向的地址被释放这样的问题. 因此就 下意识的 选择了创建并拷贝来存入vector. 这下就带来严重的问题: 题目说明公司可以随时修改careerTalk的状态, 这其实恰恰用到了指针的这个特性 . 遂芭比Q...

然后样例里也并未示例这种情况, 加上之前的样例已经对careerTalk的状态做修改, 那个样例由于没有入vector, 因而没有暴露错误. 因此de了一个多小时, 都没有能把这个bug找到.

为什么题目没有想清楚就开始做呢? 以后遇到指针, 还是要想一下.(虽然算法类的题目并不会存在这个问题, 这万恶的高程...)

debug的教训

又是一次一个多小时debug无果的经历, 这一个小时里, 我反复地看文档, 检查每一个函数的实现, 但是没有想到这样的函数组合使用导致错误.

  • debug不能只是看和模拟结果, 还是需要设计样例, 用程序来验算一致性.

  • 不仅要检查函数的实现的逻辑错误, 还要思考函数A的调用会产生什么样的结果

0x09 DSOJ W4T2 小蓝鲸比大小

  • 题目信息

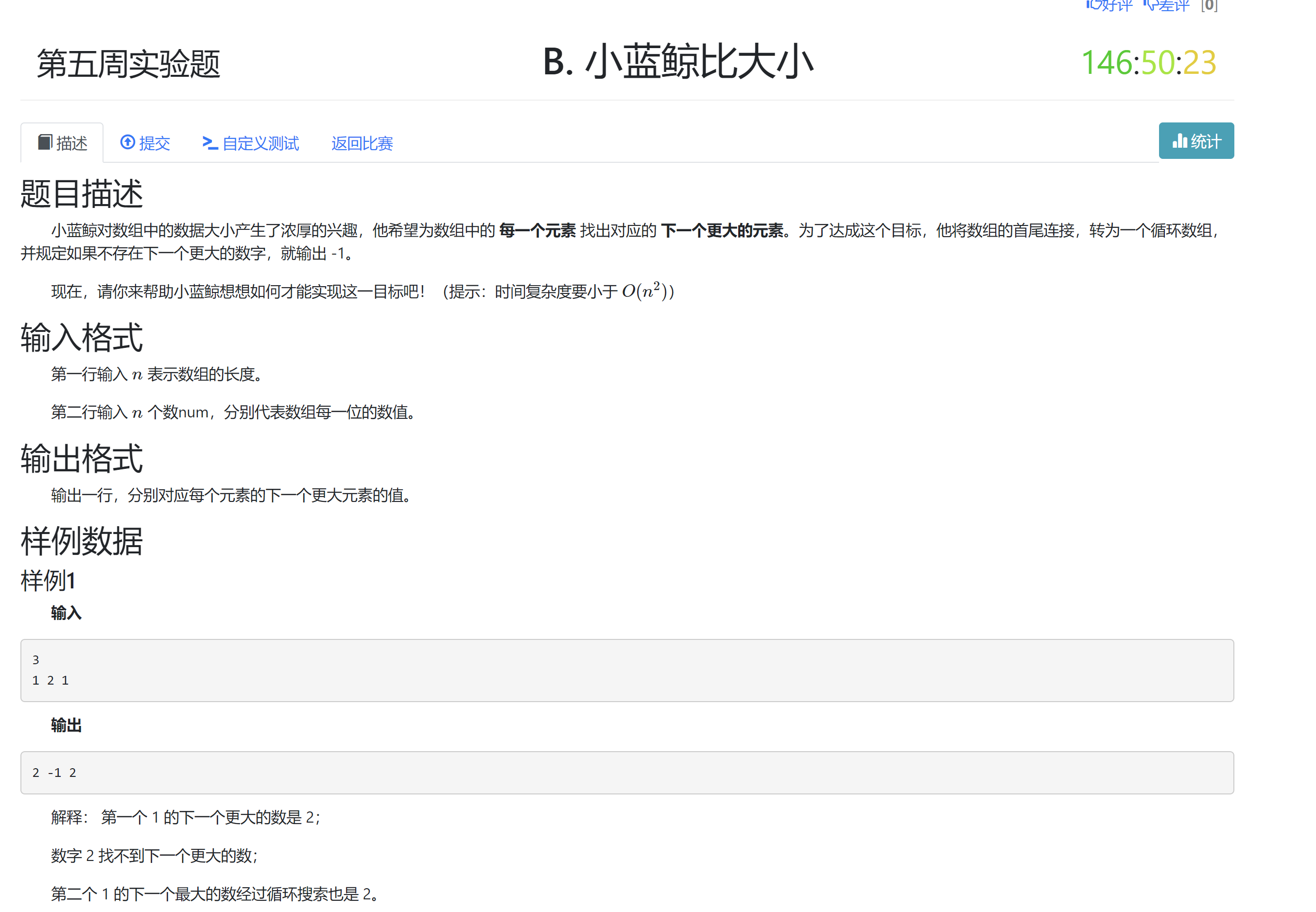
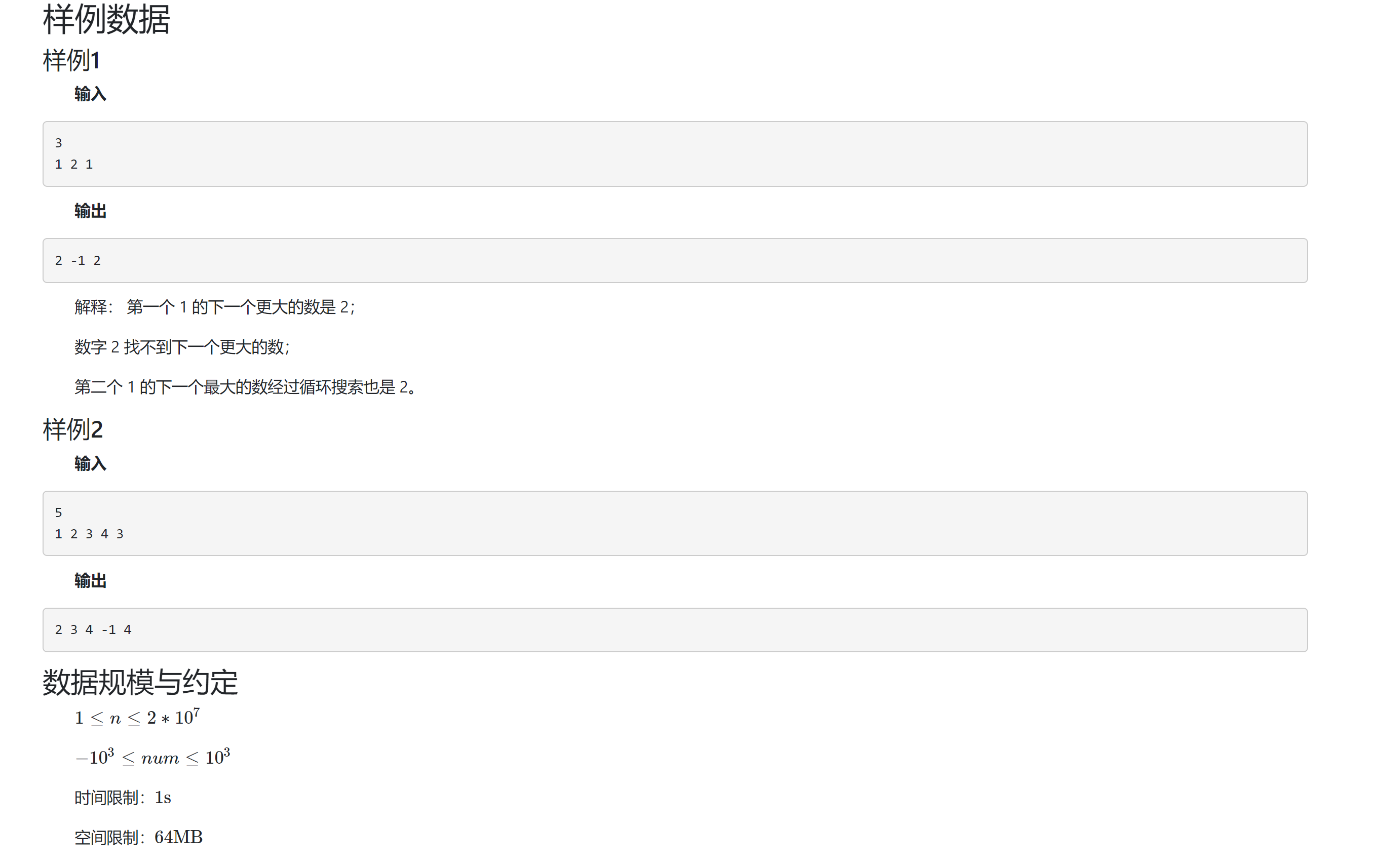
  • 题目分析

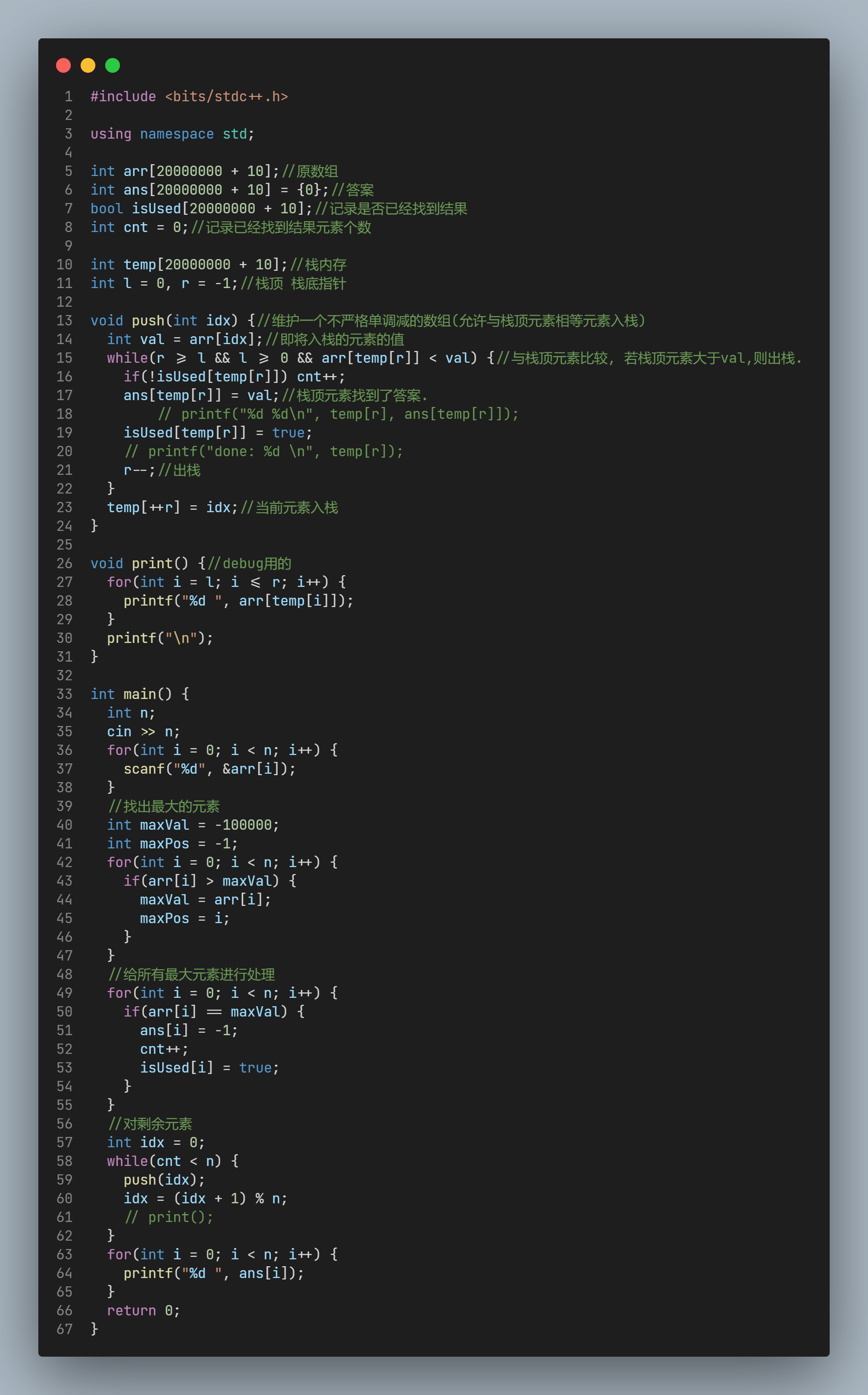
如果把单调栈的模型带入, 会发现很好的契合目标: 维护一个单调减(不严格)的单调栈, 每当元素出栈时, 必然是因为入栈元素 首次 大于该元素, 因此这个入栈元素就是该元素的答案.

首先找到整个序列里的最大元素(可能有多个, 因此需要扫描两次), 把这些元素的结果置-1, 同时标记isUsed状态.

然后依次让所有元素进栈, 当栈空时, 直接进栈; 当入栈元素值大于栈顶元素时, 栈顶元素的结果就是当前的入栈元素值, 不断重复判定直至栈顶元素值大于等于入栈元素或栈空, 入栈.

显然, 由于存在最大元素入栈, 因此一定可以使得不是最大的元素出栈; 对于最大元素, 虽然不出栈, 但是由于我们已经找到其结果, 因此不影响过程, 只会静静的躺在栈底.

复杂度及证明:

显然, 对于预备工作, 复杂度是O(N)的.

对于入栈的过程, 因为每一个元素最多只需要扫描n次就能找到其答案, 因此对于最坏的情况, 即处于序列的最后一个, 而其答案在其前面一个, 也只需要经过n次的扫描就能找到答案, 而在这之前, 一共有n次元素入栈, 因此最多只需要有2n量级的元素入栈, 而出栈操作的次数是不超过入栈次数的. 因此总复杂度为O(N).

单调栈

0x0a DSOJ W4T3 小蓝鲸找最大值(原题LeetCode)239. 滑动窗口最大值

  • 题目信息

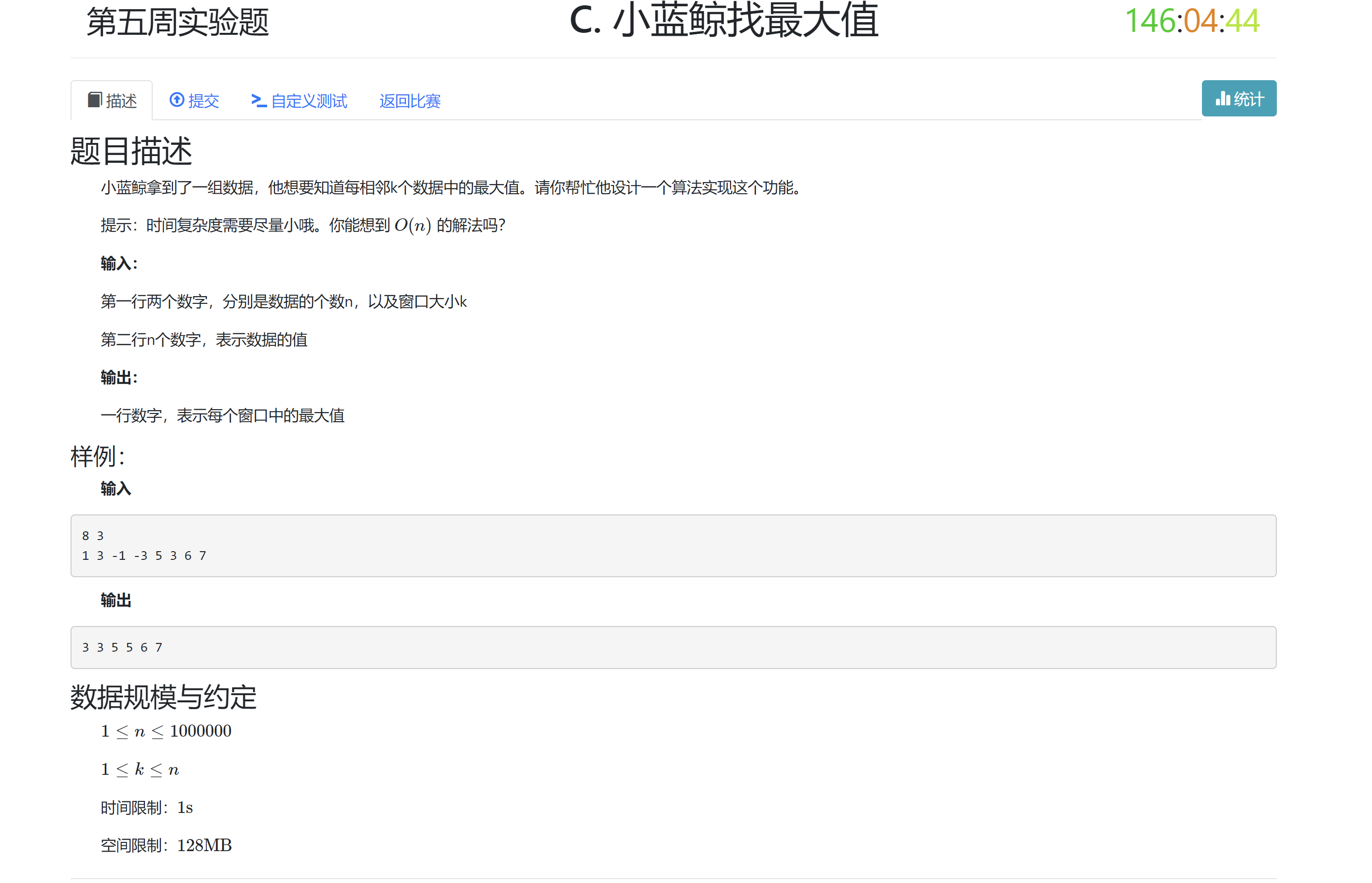
  • 题目分析

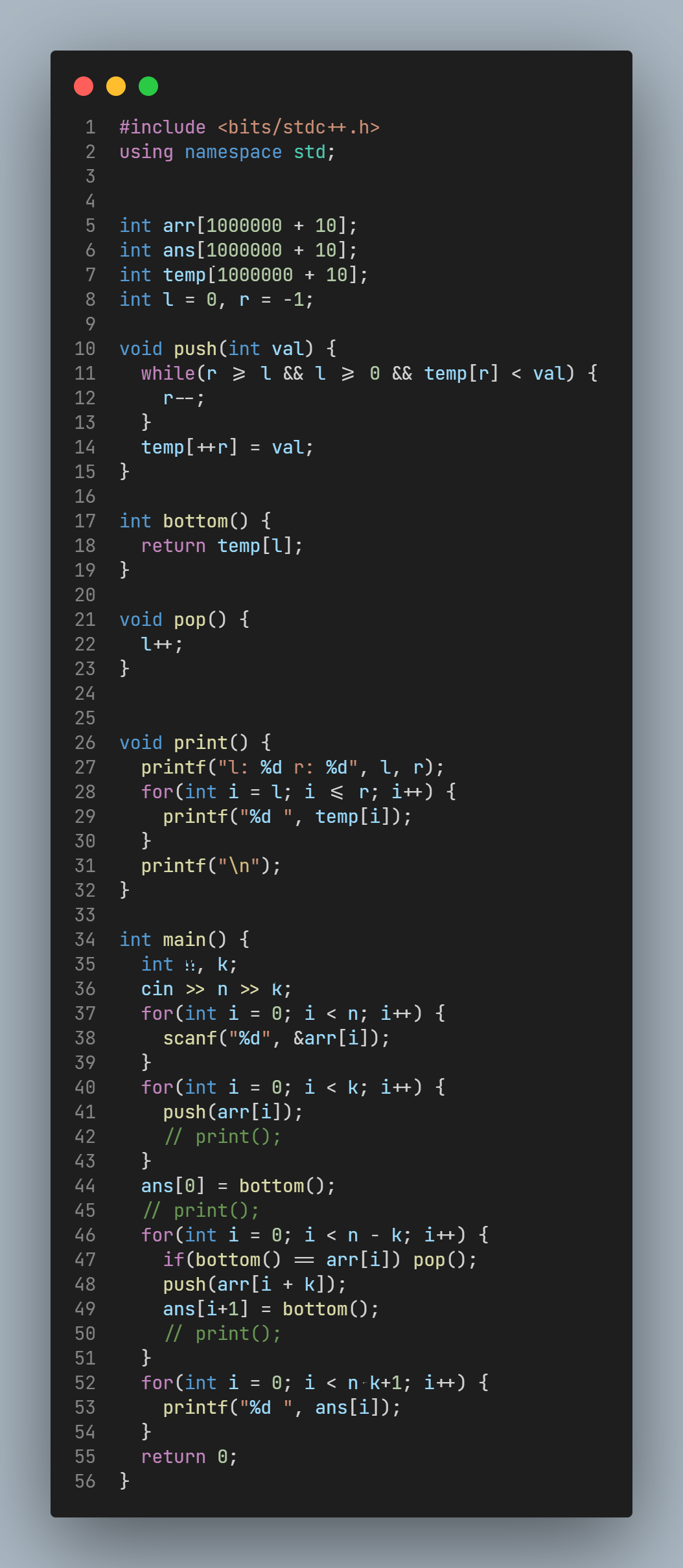
维护一个"双端队列", 这个数据结构具有栈的特性, 即允许入队和从队尾出队, 同时又可以从队首出队.

注意到一个特性, 就是在一个"滑动窗口"中, 如果后进入的元素值大于之前的所有元素, 那么之前的元素就没有存在的意义了, 因为先进滑动窗口的元素一定是先离开的, 因此若这个元素仍然存在与滑动窗口内, 则一定不会是这个滑动窗口的最大值. 这一点具备 单调栈 的特性.

对单调栈的一些思考

为什么单调栈能优化? 因为对于一个序列, 一定是若干段严格单调增和若干段不严格单调减构成, 有时候我们发现严格单调增(或者其他情况)的部分没有意义, 因此就抛弃这部分序列.

同时, 单调栈可以快速的找到第一个大于(或其他)当前元素的元素. 这也是一个很好的性质.

但是, 由于滑动窗口具有宽度限制, 达到宽度后队首元素需要出队, 因此我们需要对单调栈这个数据结构进行扩展: 当滑动窗口移动到下一个位置时, 若上一个窗口的第一个元素仍在队列中, 则需要将该元素出队, 注意到, 这个出队操作不会对后续的队列的单调性有影响, 因此每一次移动滑动窗口, 先判断需不需要将队首元素出队, 然后从队尾出队直至新元素入队时仍能满足单调性(不严格, 允许相等).每次操作结束后, 队首元素记为该滑动窗口的最大值.

显然, 这个算法是O(N)的. 下面, 讨论一些算法细节的正确性.

在 判断队首元素是否需要出队 时, 只需要比较当前队首元素是否与前一个滑动窗口的第一个元素是否值相等, 若相等就出队. 显然, 这是一个必要条件, 但是否充分呢? 即, 有没有可能, 出队的并不是上一个滑动窗口的第一个元素呢? 答案是不可能, 因为如果这个元素没有出队, 那么必然在队首, 因为这是这个队列里最早进入的元素, 而出队是满足FIFO的, 如果没有出队, 则必然在队首; 而如果这个元素已经出队, 那么必然是有比它更大的元素在它后面入队, 那么这样的话, 队首元素就必然不是它了(因为要满足单调性, 因此队首元素一定比它大才能使它出队).

单调队列

笔者之前一直以为单调队列是单调的单向队列, 但其实是可以双端push/pop的双端队列, 同时满足单调性.

入队的时候是看是否又新又好, 出队的时候是看是否太老了.

单调队列

附一张提交力扣的截图:

0x0b LGOJ 表达式的转换

  • 题目信息

见链接

  • 题目分析

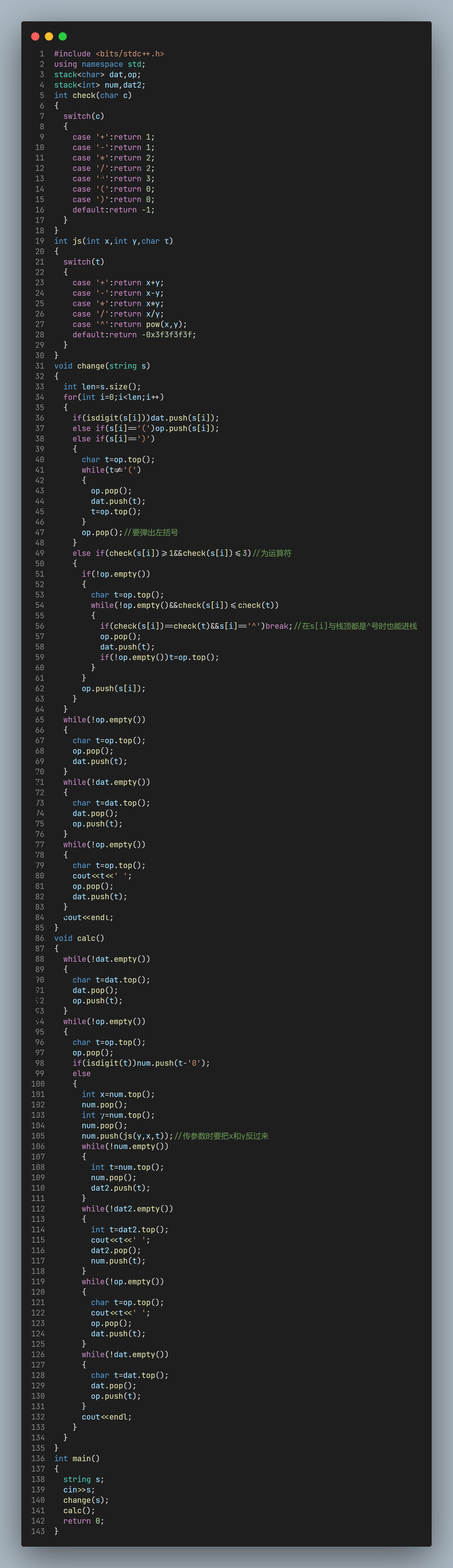
此题可以拆分成两个子问题: 1.中缀表达式->后缀表达式 2.对后缀表达式逐步计算, 显示过程

显然, 前者是比较难实现的, 后者就从左到右依次处理即可.

首先, 需要定义运算符优先级:

int check(char c)
{
    switch(c)
    {
        case '+':return 1;
        case '-':return 1;
        case '*':return 2;
        case '/':return 2;
        case '^':return 3;
        case '(':return 0;
        case ')':return 0;
        default:return -1;//程序不会执行这句，保险起见要加上
    }
}

一直弹出op栈栈顶到dat里，直到栈顶为左括号，再弹出左括号。这些也可以通过模拟得出答案。

AC, 但是不是我写的😢

0x0c DSOJ W5T4 小蓝鲸找矩阵-类似力扣:最大子矩阵

  • 题目信息

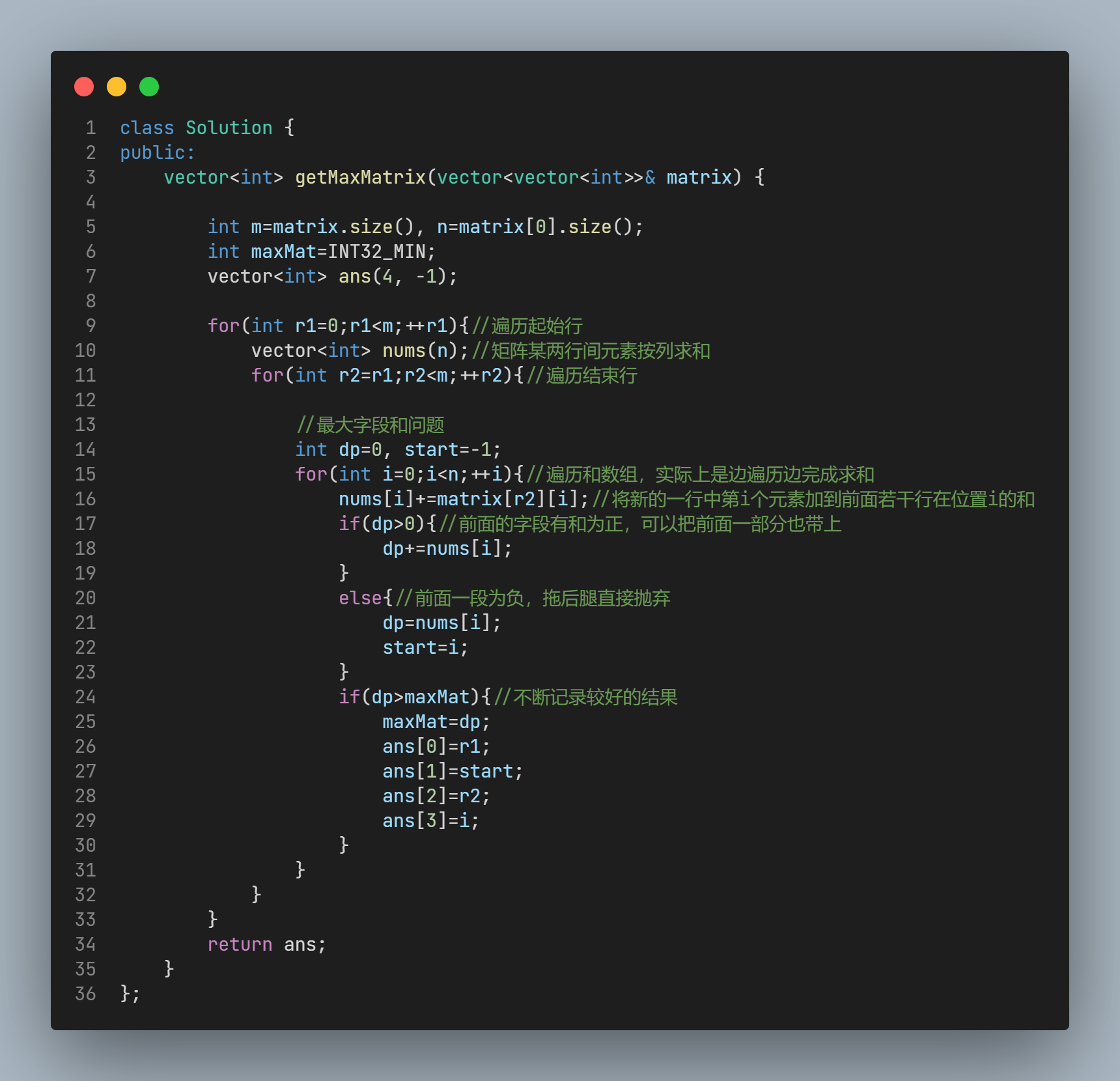
  • 题目分析

笔者想的方法复杂度只能到OO(m^2n^2), 以为要求的复杂度为O(mn), 无可奈何, 遂寄.

看了题解后的我直呼自己是sb😅.

AC

0x0d leetcode 统计定界子数组

  • 题目分析

从数据规模分析, 应该是O(n)或者O(nlogn)级别的, 而暴力的话, 复杂度至少有O(n2).

笔者的思路, 由于子数组要求连续, 因此首先对原数组进行划分, 遇到>maxk或 <minK时进行分割, 从而得到若干个minK \le a_i\le maxK的数组.

若一个子数组中只含有1个minK, 1个maxK时, 此时这个数组内符合题意的个数为这两个数的位置与边界之差的乘积.

但是如果一个子数组里有多个minK或maxK呢? 看起来是一个容斥原理的问题, 笔者在这里就卡关了.

  • 参考思路

来自力扣用户灵茶山艾府.

参考代码 
class Solution {
public:
long long countSubarrays(vector<int> &nums, int min_k, int max_k) {
    long long ans = 0L;
    int n = nums.size(), min_i = -1, max_i = -1, i0 = -1;
    for (int i = 0; i < n; ++i) {
        int x = nums[i];
        if (x == min_k) min_i = i;
        if (x == max_k) max_i = i;
        if (x < min_k || x > max_k) i0 = i; // 子数组不能包含 nums[i0]
        ans += max(min(min_i, max_i) - i0, 0);
    }
    return ans;
}

0x0e W7T1 KMP模板题

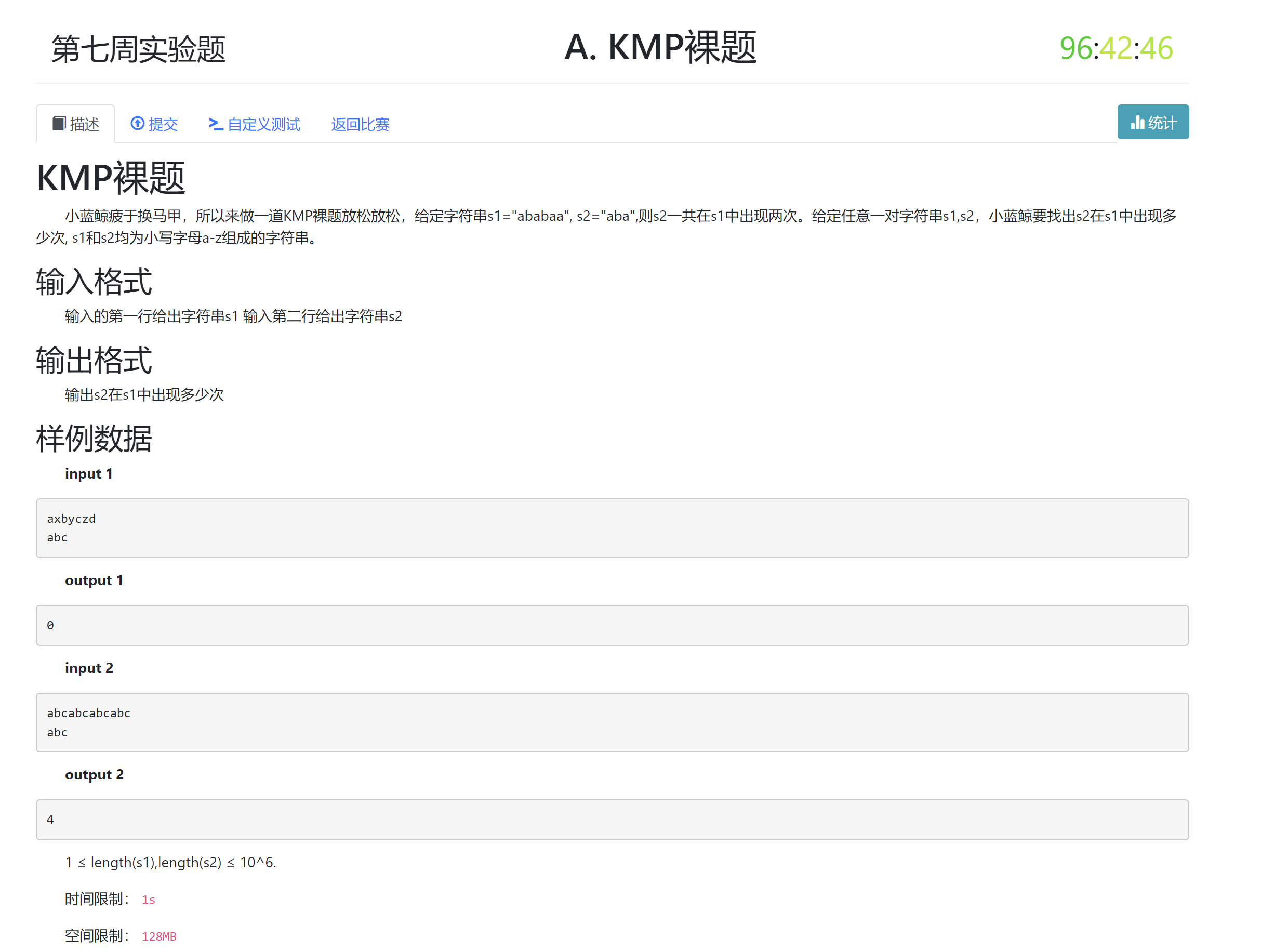
  • 题目信息

  • 题目分析

笔者第一遍直接选择copy了标程, 后来于心有愧, 决定尝试自己写了一遍KMP算法, 没想到竟然一遍过.

虽然之前已经看过不少文章, 听过老师讲解KMP算法, 但还是不如自己手推一遍的效果好. 笔者就分享一下自己手推KMP算法的思路吧.

AC, 但不是标程, 笔者自己手推的

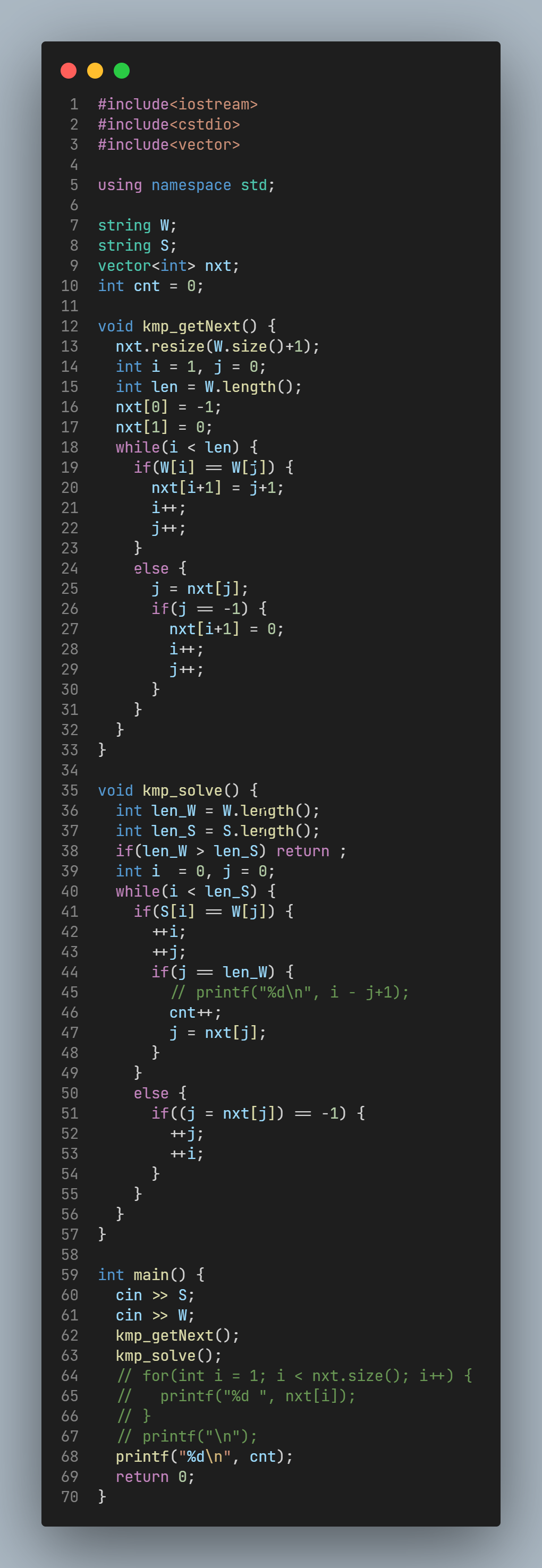
笔者手推KMP思路

  • 任务: 给定两个串S和W, 要求找到S中所有匹配W的位置.

  • 约定: i是S的指针, j是W的指针.

首先, 我们先不去想KMP, 想想BF怎么做: 无非就是遍历S的每一个idx作为起点, 然后依次匹配W中的每个字符, 直到失配或匹配成功. 这个算法是\Theta(mn)的, 因为考虑最坏的情况, 例如S = aaaaaaaaa, W = aaaaa, 这样的情况下, 算法的下界就达到了\Omega(mn), 而显然上界是O(mn)的, 因此这个算法的复杂度是mn量级的.

不难发现, 其中存在的重复计算的信息在于, 当次匹配失败或成功后, 下一次不一定要从W的第一个元素开始匹配, 而是可以跳过一些字符 , 这就是KMP算法的核心. 具体来说, 我们可以假设下一次匹配时, j先放在0的位置, 然后尝试整体左移, 即j++, 看看能不能使得移到左边的部分同样匹配成功. 在手动模拟一遍后, 容易发现, 能移动的最大距离, 就是W[0-j-1]这个字符串的最大公共前后缀. 每一次i++时, j总是跳过这个最大的公共前后缀的长度, 即j = next[j].

好的, 先不管kmp_getNext()函数怎么写, 假设我们已经得到了next[], 那么, 怎么进行S与W的匹配呢?

遍历i, j从0开始, 如果S[i] == W[j]则++i, ++j, 并判断一下j == len_W?, 如果是的话, 即匹配成功, ++i, 那么j怎么变化呢? 当然也需要利用之前匹配的全部信息, 因此j = next[j].

如果S[i] != W[j], 即发生失配, 这时候, 能不能就宣告i开头的这个S子串就失配呢? 别忘了, 我们并不是将两个串对齐比较的, W串上来就左移了, 根据next[j]的定义, next[j]就是j发生失配后, j应该移动到的地方, 因此j = next[j], 那如果j一直回退, 直到回退到j == -1时, 就说明从0开始都匹配失败了, 至此, 才宣告这个S[i]开头的子串彻底失配, ++i, ++j.

最后, 来写kmp_getNext()吧. 时刻把握住两个基本定义: next[j] 是j发生失配时, j重定向的idx. 而从原理上说, next[j]是W[0-j-1]这个子串的最大 真 前后缀(即不能等于自己)数 + 1, 就是, 发生失配后, 尽可能的跳过必定匹配的部分(如果等于自己的话, 那就不会跳过了)

因此next[0] = -1, next[1] = 0.

注意到, next[j]的值其实是与W[j]无关的, 只与W[0-j-1]有关.

比较神奇的是, 从左到右依次尝试匹配自己的过程, 就是求最大公共前后缀的过程, 这也就是kmp_getNext与kmp_solve神似的原因. 至于具体的求解过程就不再复述.

0x0f W7T3 小蓝鲸找路径

  • 题目信息

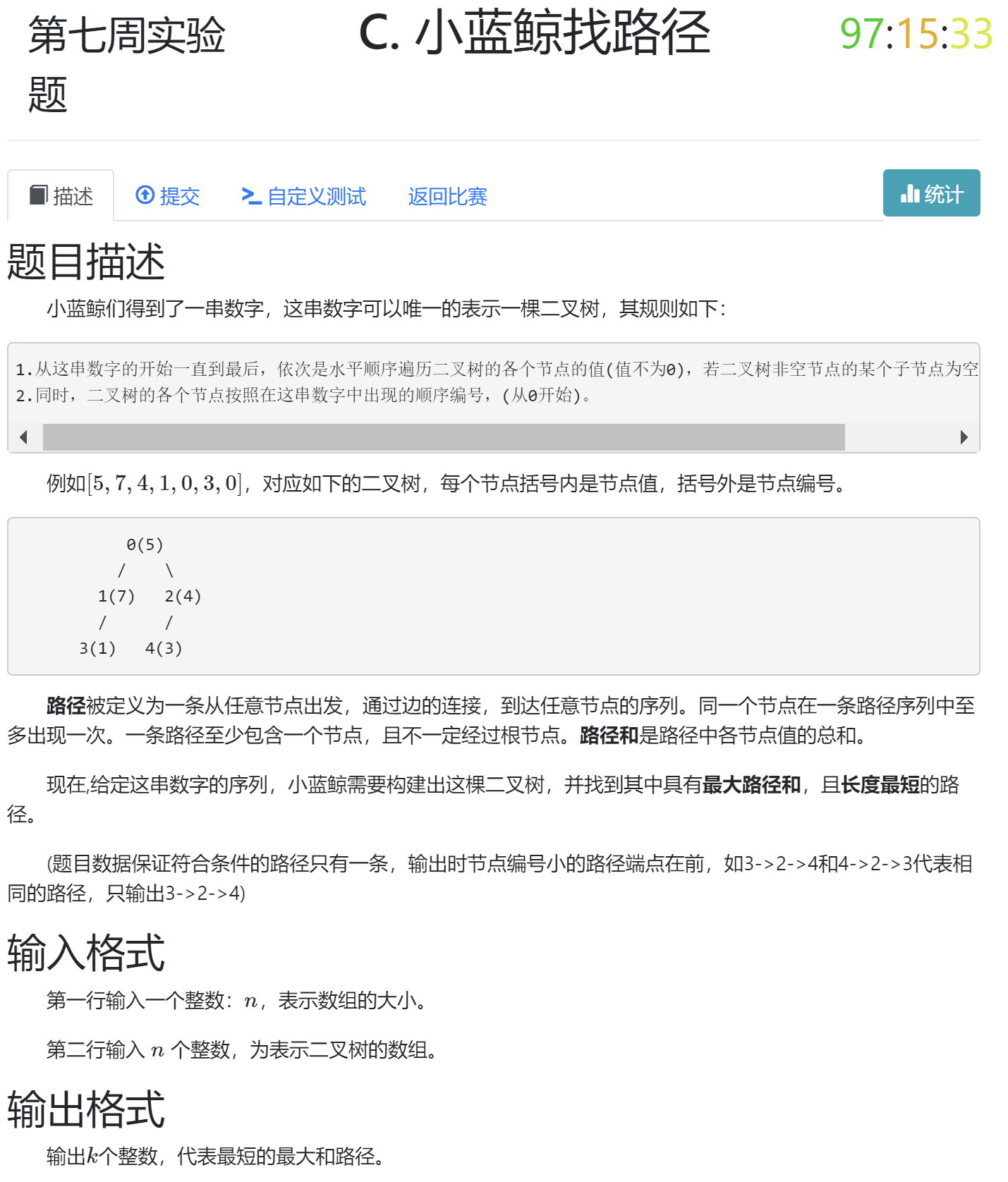
  • 题目分析

很明显的缝合题, 分成两个任务: 1. 根据层序遍历的序列建树 2. 根据二叉树求树上的最大路径和的路径.

  • 对于建树的部分, 就是基本的利用队列的思想, 每次取队首的一个树的节点, 创建其左右子节点后加入队列, 注意这题的输入并不是将每一层所有的节点全部输入, 对于已经确定不存在的二叉树节点, 就不再输入0来表示空节点了, 这是一个小坑. 此外的部分就是按照这个规则做即可.

  • 问题的难点在于怎么样寻找最大路径和.

[观察1]注意到对于二叉树, 路径只有两种:

  • A:从一个节点出发, 一路向下, 每次选择左右子节点中的一个;
  • B:以某一个节点作为中转站, 连接两条向下的路径, 形成一个\wedge形状的路径. 于是, 我们不妨将这样一个节点作为这种路径的标记.容易发现, B类路径, 其实是中转站节点的左右子节点的A类路径连接连接得到的.

也就是说, 对于一个节点, 维护两种AB两种最大路径, 每次得到新的路径时, 尝试更新即可.

[观察2]注意到, 对于A类路径, 节点M和它的子节点N的路径是具有继承关系的, 如果N的A路径和大于零, 则显然, M的A类路径就是将N的A类路径连接上M节点自己; 如果N的A路径和小于零, 则舍弃, M的A类路径就是M节点自己.这一点就是动态规划的思想, 其实就等价于一维的最大子数组问题.

[观察3]对于B类路径, 显然只存在于某一个节点的左右子节点都存在, 且各自的A类路径和都大于0(不包含等于, 因为题目要求路径节点数尽可能少)时, 将两个A类路径连接起来, 才可能得到一个更大的路径和.

到这里, 这道题目的思路就基本出来了: 对于某一个节点, 先递归求解其子节点的A类和B类最大路径和, 然后当前节点的A类路径和等于\max\{左子节点的A类路径和, 右子节点的A类路径和, 0\} + 当前节点的权值, B类路径和就是将两个路径和连起来(如果存在且可能有意义的话). 完成当前节点的计算后, 尝试更新最大的路径和并返回. 对于递归的终止条件, 即叶节点, 显然, 其A类的路径和就是自己的权值, 不存在B类路径和.

最后还有一个问题, 由于题目要求输出最大和的路径, 怎么记录这个路径呢?

比较容易想到的方法就是, 对于每一个节点, 都维护一个存放路径的容器, 考虑到存在正向和逆向输出的需求, 选择使用deque会比较好写一点. 这个容器也随着递归的过程, 不断继承, 不断更新最大的路径即可.

优化

其实不需要记录全部路径的, 对于每一个节点, 只需要维护路径的起始点即可, 也可以再维护一下这样的路径经过的节点数, 最后只需要在树上跑一下就可以得到完整的路径.

这样的话, 可以将空间复杂度从O(M\log(M))降低到O(M).

总体评价的话, 题目本身的思想还是比较经典的dp问题, 不过实现起来确实挺麻烦的, 非常考验码力和debug的能力.

一个没有独立de出来的bug

由于题目要求, 对于路径和相等的两条路径, 需要输出路径上节点数较少的一条.

本人在写update的时候, 注意到了这一点, 然而在递归的内部做选择的时候, 却忘记了, 导致90分迟迟不能AC. 又因为本题造数据比较艰难, 笔者在debug的过程中始终没有造出这样的样例. 最后就找不到问题.

教训

对于这样的比较难找的corner case, 如果反复造数据也找不到问题, 可能是因为忽略了题目要求的部分规则, 这样的话, 造数据就也不会刻意造这样的样例, 自然也就找不到问题了. 所以这种情况下, 就需要看一遍代码, 理一遍自己的思路, 和题目要求对比, 寻找逻辑上的疏忽.

AC

写的时候遇到的一个要点

如果在函数外部创建的空指针, 在函数内部开辟空间时, 函数传参要写成void foo(TreeNode *& root)(想想为什么?)

此外, 在创建树或者链表时, 一定是先开辟子节点空间, 将父子连起来(不能子是nullptr), 再将父弹出或者子存入.

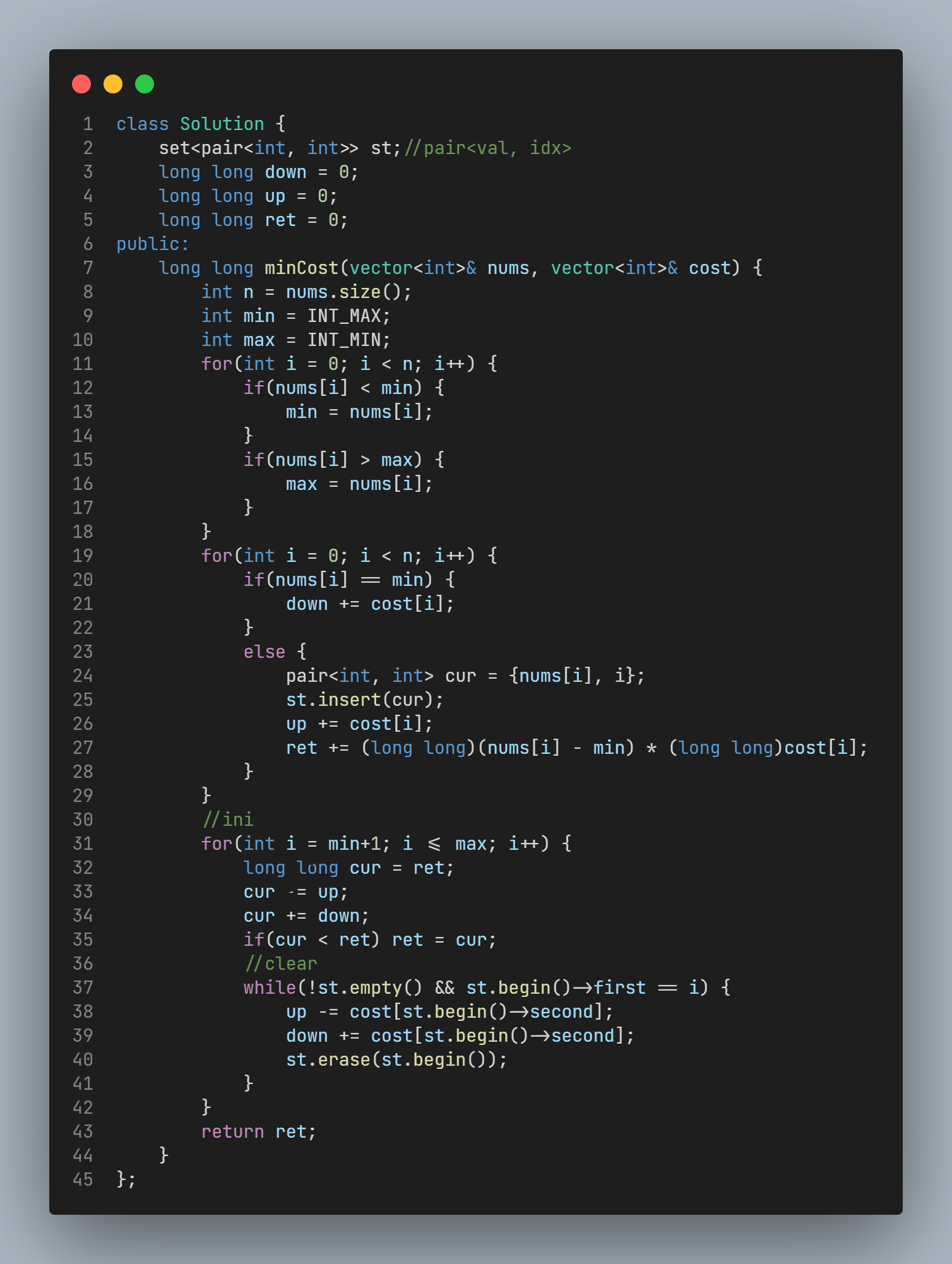
0x10 力扣第316周周赛T3 使数组相等的最小开销

  • 题目信息

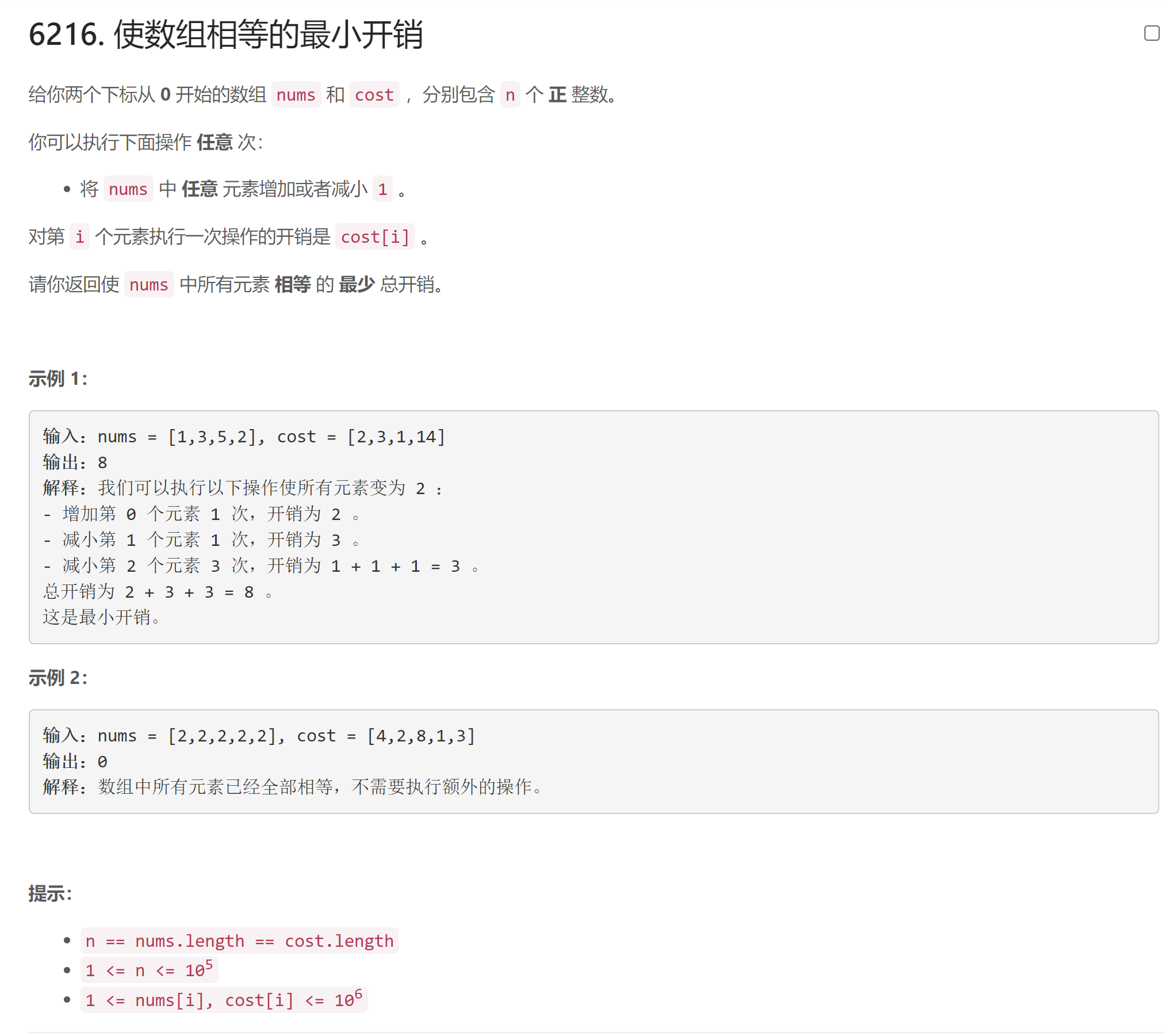
笔者第一次AK周赛, 恰好逢上"双困难题", 最后拿到的名次也很有纪念意义😆

  • 题目分析

抄一份题解吧, 与笔者方法略有差异.

笔者代码

0x11 DSOJ W8T1 线索二叉树

  • 题目信息

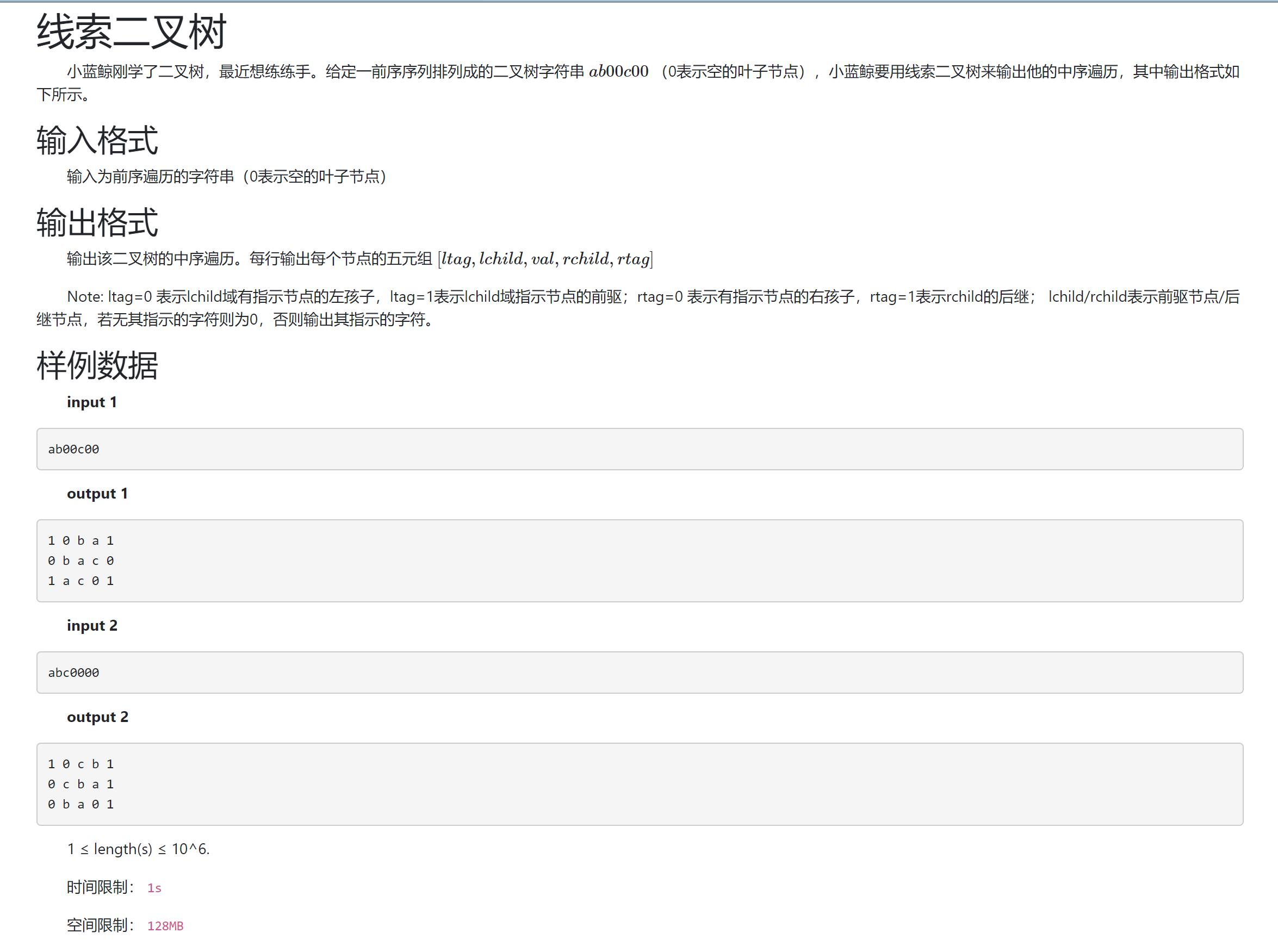
  • 题目分析

感觉没什么用?

0x12 DSOJ W8T3 小蓝鲸装监控

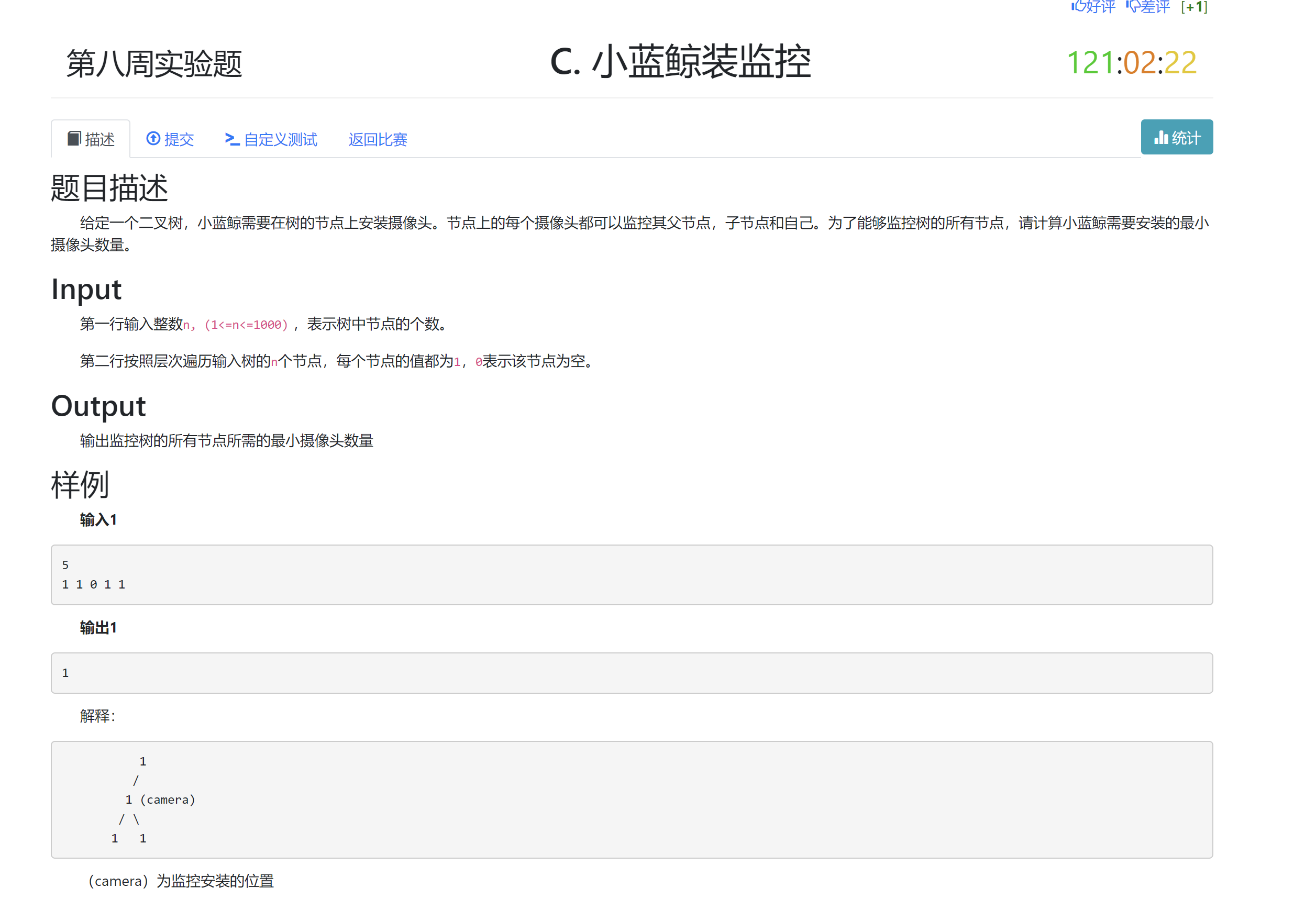
  • 题目信息

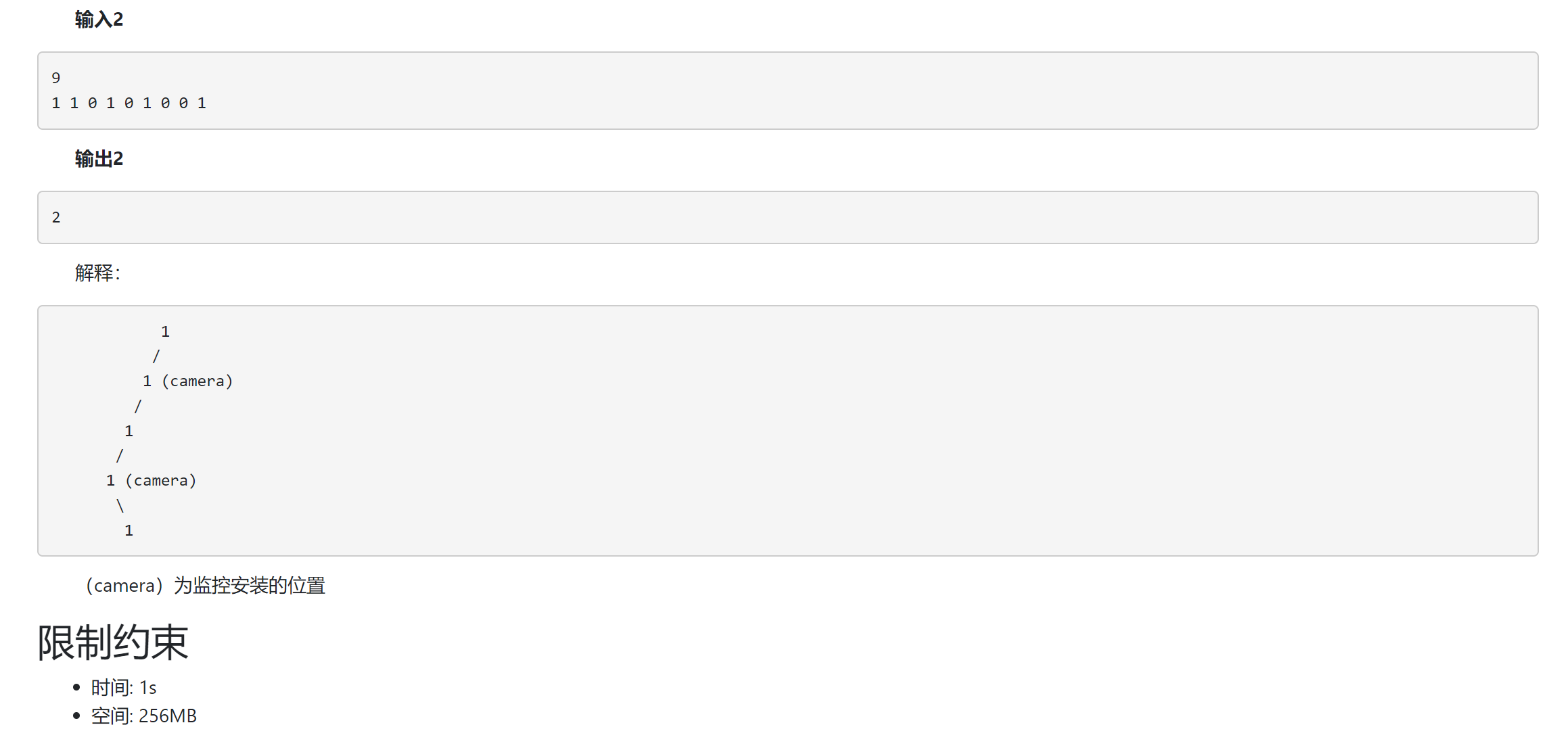
  • 题目分析

个人觉得这题出的还是挺好的, 虽然算法的实质并不难, 就是一个DFS, 但是很容易让人想复杂.这题对DFS和动态规划都有考察, 还是挺好的.

首先需要一些观察.

[观察1]容易发现, 虽然对于一种情况, 最少的监控数量是确定的, 但是具体的监控的安装位置却并不唯一. 例如, 对于样例2, 上面的一个监控既可以安装在根节点, 也可以安装在根节点的左子节点.

那么, 这些解之间, 有没有优劣之分?

[观察2]不难发现, 如果叶子节点和其父节点都可以安装监控的情况下, 安装在父节点上会"更好". 因为如果父节点还有父节点的话, 就可以多覆盖到一个节点的. 对于多种解都可以得到最优答案的情况, 我们总是可以选择逐步的最优解, 这样得到的结果一定是最优的. 这样, 我们就得到了最底层的安装策略.

下面要思考的问题: 按照什么顺序进行安装?

[观察3]手推一些较为复杂的情形, 会发现, 从叶节点, 逐步向上安排是一种较好的方案. 对于已经安排过监控的节点, 如果其所有子节点以及父节点都已经被覆盖到, 那么在计数增加后, 可以删去这些节点, 并不影响上面的树的安排.

有了这些铺垫, 下面就需要一些灵感/经验了.

我们可以对这棵树进行DFS, 自底向上逐渐安装. 需要用到dp的思想, 将对每一个节点的遍历作为一个状态, 需要处理的是判定当前节点是否需要安装监控. 可以证明, 当前节点是否需要安装监控, 只与其子节点和父节点(如果有的话)相关. 下面给出具体的递归判定策略.

判定策略

  • 如果当前节点是叶节点,

    • 如果有父节点, 则不安装, (因为一定可以在其父节点上安装, 这样更优)

    • 如果没有, 则安装.

  • 对于非叶节点, 则就说明一定有子节点了. 需要连同子节点的状态一起判断.

    • 如果子节点至少有一个未被覆盖, 则当前节点一定需要安装

    • 如果当前节点也已经被覆盖了, 那么, 也就可以被去掉, 不需要安装

    • 如果自身没有被覆盖的话, 那么就等效于一个叶子节点了, 这时候判断如果有父亲节点的话, 就不安装; 如果没有, 那就安装.

由于二叉树DFS的特性, 一定是自底向上, 而不同子树之间也互不影响, 因此先后处理顺序不影响判定, 这样就完美符合了整个安排的策略. 代码也就差不多了.

AC

0x13 DSOJ 小蓝鲸分组

  • 题目信息

  • 题目分析

考虑两个元素a, b, 如果a不喜欢b, 那么a, b不能分到一个组, 而b与b讨厌的人也不能分到一个组, 因为因为只有两个组, 因此a需要与b讨厌的人分到一个组.

这里, 注意到我们需要维护的不仅是a应该与哪些人一组, 还有a不应该与哪些人一组, 因此使用{拓展并查集}的思想, 将并查集的域拓展为2\times n, 其中, 前n格存放0-i应该与哪些人一组, 后n格存放0-i不应该与哪些人一组.

那么, 怎么判断是否能够满足呢? 显然, 条件是: 两个彼此讨厌的人具有相同的分组归属.

AC

0x14 APOJ 又是指针的问题

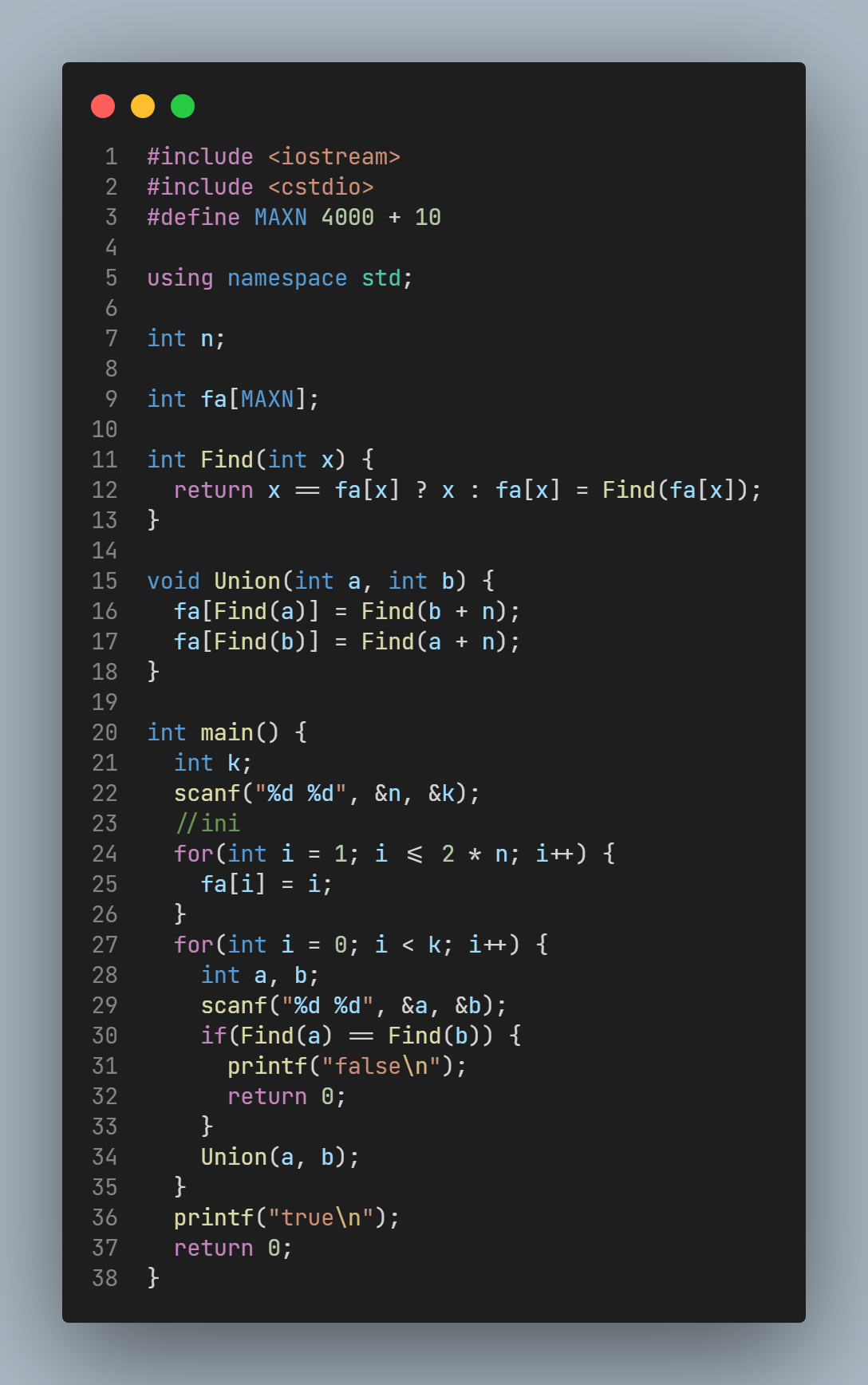
来看一段很简单的代码:

Book *Platform::borrowBook(string name)
{
// TODO
Book *ret = NULL;
for (int i = 0; i < this->books.size(); i++)
{
  if (this->books[i]->getName() == name && this->books[i]->isOnShelf())
  {
    if (ret == NULL)
      ret = books[i];
    else if (books[i]->getPrice() < ret->getPrice())
      ret = books[i];
  }
}
this->num_of_books--;
ret->setState(false);
return ret;
}

Book *Platform::borrowBook(string name)
{
  // TODO
  Book *ret = NULL;
  for (int i = 0; i < this->books.size(); i++)
  {
    if (this->books[i]->getName() == name && this->books[i]->isOnShelf())
    {
      if (ret == NULL)
        ret = books[i];
      else if (books[i]->getPrice() < ret->getPrice())
        ret = books[i];
    }
  }
  if (ret != NULL)
  {
    this->num_of_books--;
    ret->setState(false);
  }
  return ret;
}

明显的错误

对于可能返回nullptr的结果, 如果在返回前还需要对结果通过指针的方式进行访问, 那么显然需要做的事情就是对指针是否问空进行判断, 否则就会发生Runtime Error, 其实是很显然的错误, 但是笔者却因此盯着短短几十行代码de了40min, 又是惨痛的教训.

教训

对于指针的操作一定要先想一想能不能访问!!! 留意bad pointers!!!

0x15 DSOJ W12T2 小蓝鲸找数字

  • 题目信息

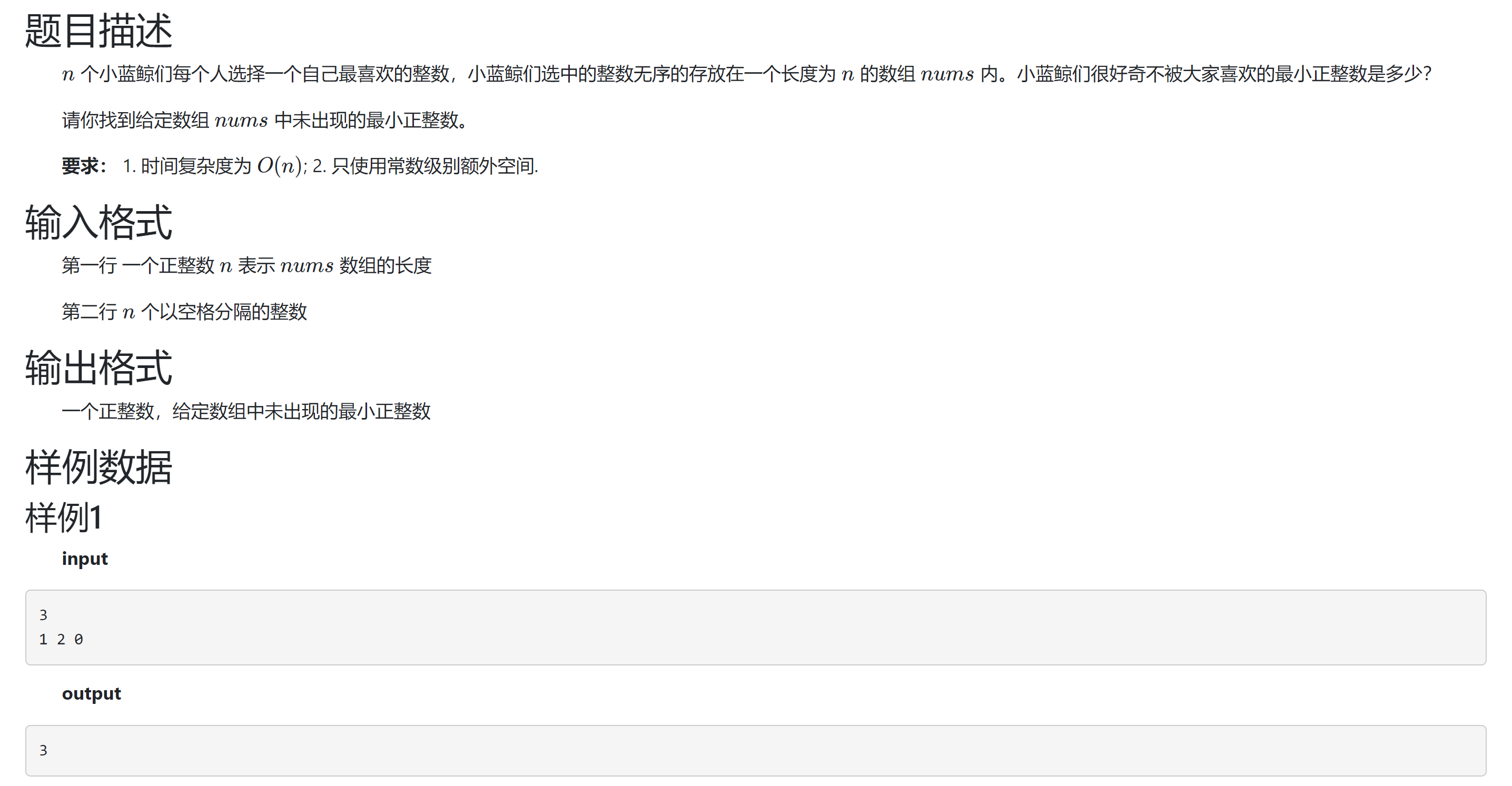
  • 题目分析

笨笨的笔者花了一个多小时也没有能够做出O(N)的方法, (当然也被*只用常数的额外空间*坑了), 最后只能用O(NlogN)的方法卡过.

an essential note

需要注意到, 这道题的答案一定是在[1,n]内的.

在注意到这一点后, 下面的操作仍然需要一些技巧. 主要是受到*常数的额外空间*所限.

方法一 交换法:

给对所有的元素尝试"归位", 也就是将数字i放到第i个位置上, 只能通过交换两个元素的方法来完成这件事情, 但是需要注意, 交换后, 原先在第i位上的元素同样需要"归位". 在尝试将所有的元素归位后, 第一个没有归位的元素对应缺失元素就是答案.

此外, 由于题目输入的元素可能不符合要求, 这些数字我们并不关心, 可以都改为一个大于n的数输入.

时间复杂度分析: 由于每个元素至多被归位一次, 因此是O(N)的.

方法二 构建小顶堆:

注意到通过一次性将数组转化堆(heapify)操作的复杂度是O(N), 因此直接将原数组heapify, 然后不断pop()?

0x16 DSOJ W12T3 奇怪的二叉树

  • 题目信息

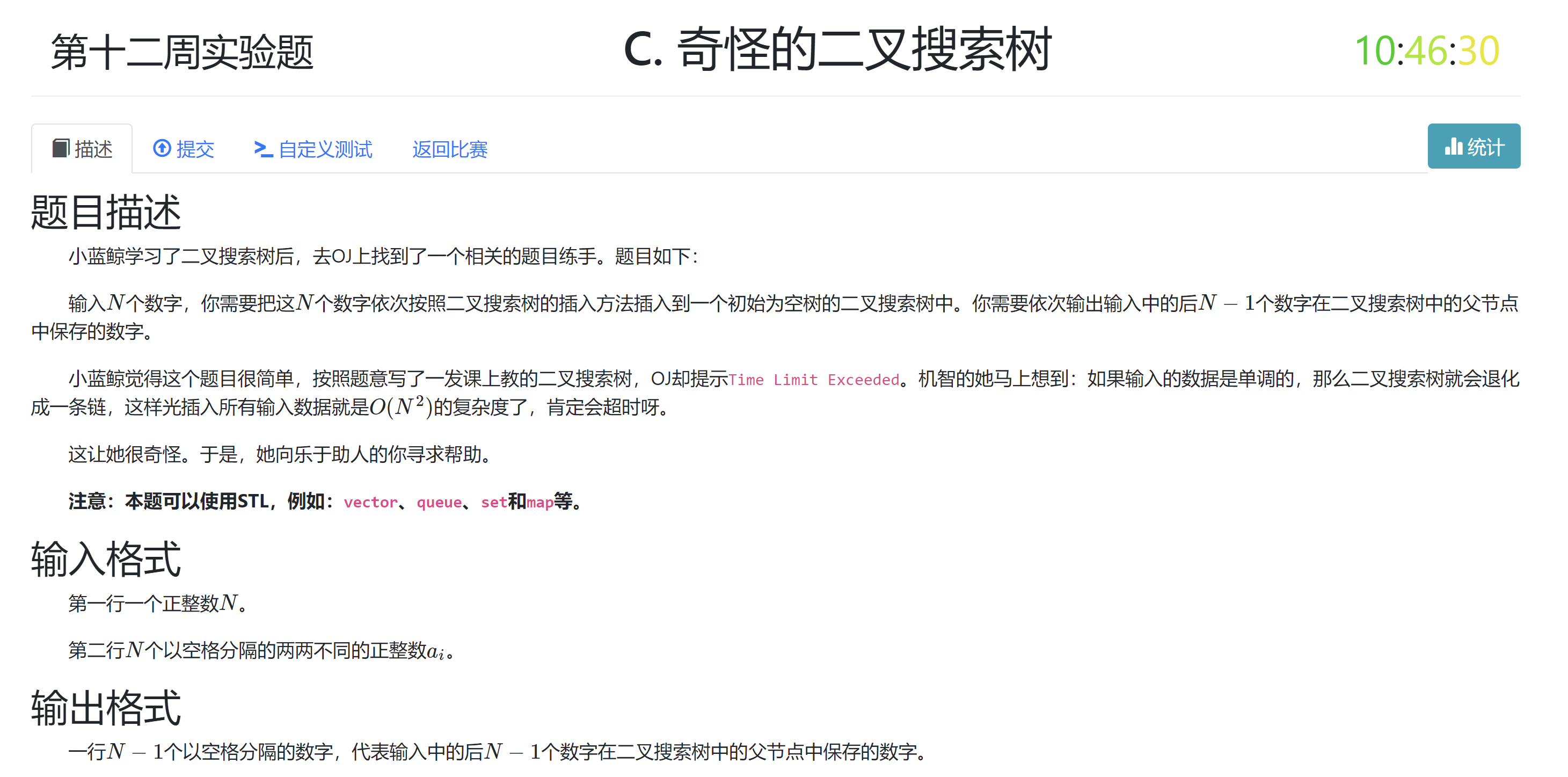
  • 题目分析

利用到二叉搜索树的一个性质: 如果将二叉树的中序遍历转化为一个数组, 每次插入的新元素的位置一定是在第一个大于它的元素和最后一个小于它的元素之间的, 而作为二叉树, 每次插入的元素一定是在某个节点的左孩子或者右孩子, 同时作为一个叶子节点, 因此从序列的角度来看, 一定是在父亲节点的左边或者右边一个. 因此在序列中插入后, 当前节点的父亲节点只能是与其相邻的两个节点(注意, 如果是在两端的话, 只有一个)之一, 那么简单使用排除法(父亲节点的子节点不能已经有孩子了), 就很容易找到答案了

复杂度分析: 通过二分法插入, 总的时间复杂度为O(\sum_{i=1}^nlog i) = O(n\log n).

上式的证明

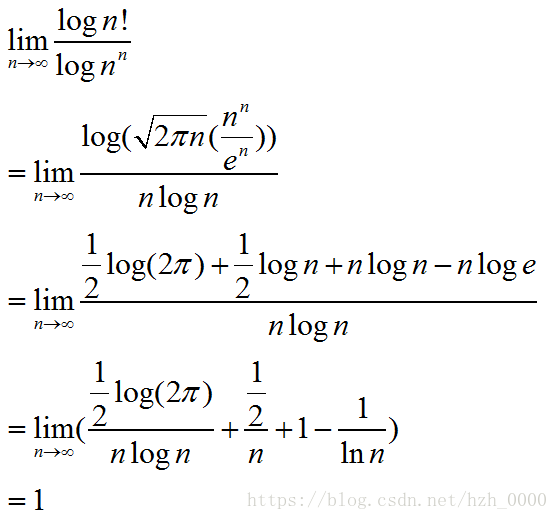
0x17 力扣第322周周赛T4 将节点分成尽可能多的组

  • 题目信息

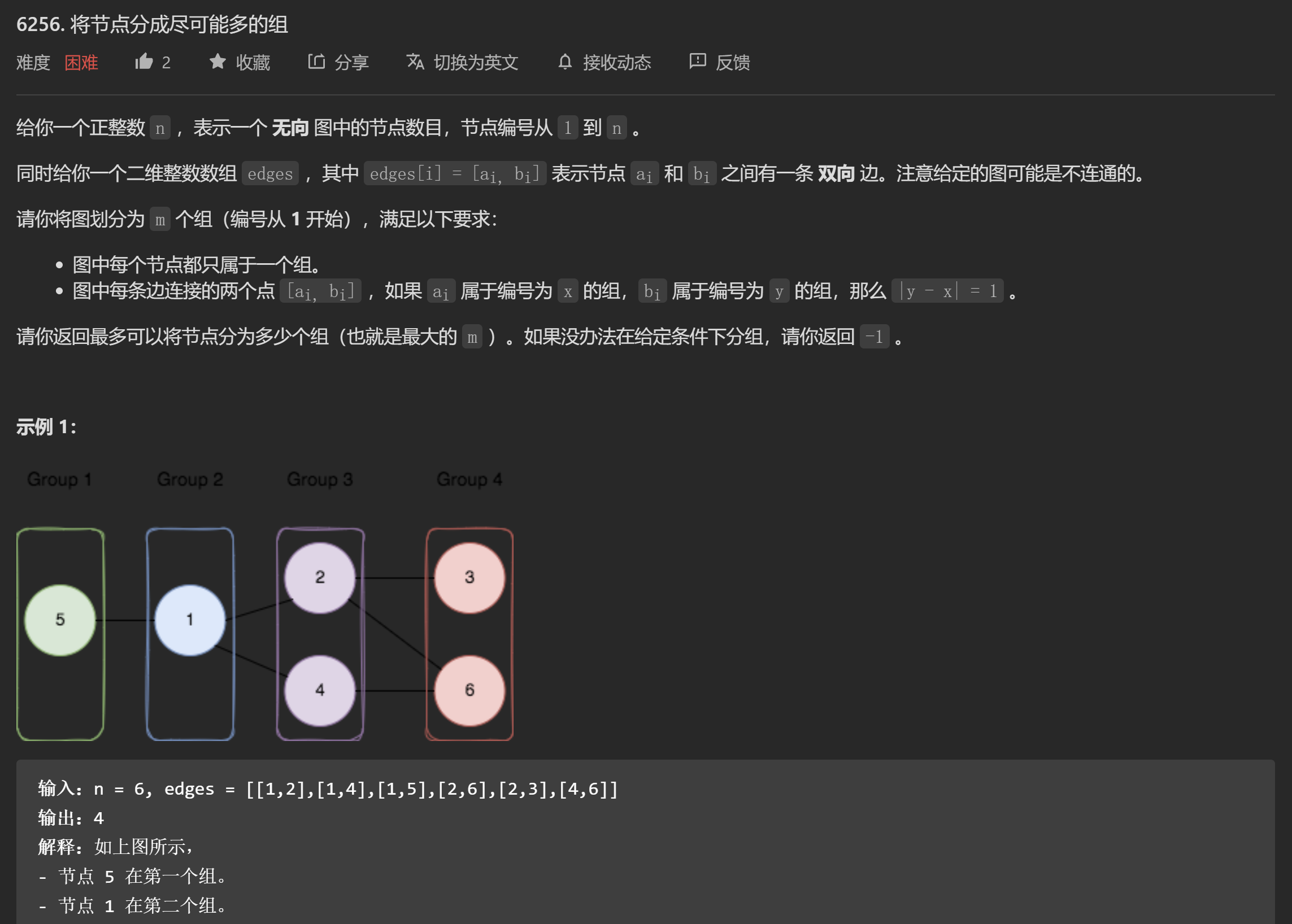
(详情见网址页面)

  • 题目分析

说几句

之前打过的周赛里, 图论几乎没有涉及过, 这次T3T4都是有涉及, 题目质量会更高一些. 从最终做出来的人数(<300人)也能说明.

笔者花了半个多小时写出来了第一个版本, 在调试修改过后, 最终TLE告终. 赛后看了题解后, 将其中的图存储方式由邻接矩阵改为邻接表, 竟然就通过了....

简直气死, 说明笔者对自己的代码的复杂度的分析能力还是不足, 其实我写这题的时候都没有太关注复杂度, 只是看到n并不算大, 就不再细细分析自己的算法的复杂度了.

值得思考的问题是, 为什么使用邻接表和邻接矩阵, 会在时间复杂度上产生这么大的差距?

下面来分析一下题目.

我们来手动模拟一下这个划分的过程. 首先从一个点a开始, 显然, 与这个点直接相连的点需要划分到其他的组, 但是, 与这些点相连的点呢? 可不可以分到与a相同的组? 答案是可以的. 因此, 不难发现一个 规则 : 如果我们对这些顶点用两种颜色进行染色, 要求相邻的顶点不同色, 只要当所有顶点都被染色后, 仍然满足这个性质, 那么就存在合法的分组, 反之则不能.

证明:

通过染色的方式, 说明了一个 性质 : 如果两个顶点相邻, 则这两个顶点一定不能分到同一个组, 而颜色也不同. 反过来说, 逆否命题: 如果两个顶点的颜色相同, 那么一定不存在边相连.

若不满足这个规则, 则说明存在两个相邻的顶点, 颜色是相同的, 那这就违背了上述的性质.

如果满足这个规则( 注意 : 这是前提), 那么就能给出一种分组的方式:

  • 任取当前连通分量中的一个点, 先将这个点分为一组;

  • 然后将所有与其相连的点分到下一组, 显然这些点的颜色都是相同的, 因此不会有边相连.

  • 同样的, 将这些点相邻的顶点分到下一组, 同样也满足不存在边相连.

  • 以此类推, 直到所有的顶点都分完, 我们就得到了一组合法的分配.

形象的说, 就像是将这个图从一个顶点开始, 从左到右将整个图"捋了一遍". 读者可以自己尝试一下.

那么, 下一个问题是, 对于一个连通分量, 我们怎么得到最大的分组数呢?

这个问题很难解决, 但是, 我们可以肯定的是: 如果对一个连通分量的每一个点都作为起始点来"捋一遍", 正确的答案一定就在这些方案之中.

证明: 不难发现, 如果以某一个顶点作为起始点(也就是最左边的一组, 只有这一个点), 上述方案会得到最大的结果.

如果起始组有多个点的话, 将其中的一点向右边的组"摆动"(即分到右边的组), 一定不会使得分组的组数变小. 也就是说, 最左边的组只有一个点的分组结果, 组数是大于等于其他情况的(最左边的组有超过一个点). 所以我们只要在 最左边组只有一个点的分配方案中找最大值, 就一定是全部方案的最大值.

所以, 至此我们有了解题的思路:

  • 遍历所有的顶点, 以该顶点作为起始点, 按照上述方案进行分配, 一遍分配, 一遍判断是否满足一开始提到的规则.
  • 从实现上来说, 可以采用BFS的方式, 用一个cnt记录组数, 用flag数组记录每个顶点的颜色, 未染色的点用-1表示, 0, 1代表两种不同的染色. 在BFS的过程中, 如果遇到未染色的点, 那么就flag[i] = cnt % 2标记, 同时将该点加入队列; 如果遇到已经遍历过的点, 那么必然已经被染色, 如果颜色与要染的颜色(即cnt % 2)不同, 那就说明矛盾, 不能满足规则, 也就是说, 不存在分配方案, 返回-1.

  • 最后, 当队列为空时, 说明连通分量中的所有点都被染色, 且不存在矛盾, 因此cnt有效, 就是一种可行的分组数.

  • 完成所有的点的遍历后, 我们就得到了每一个连通分量以任意顶点为起始点的组数. 那么只要将不同的连通分量的分组情况的最大值相加即可.

  • 那么, 怎么知道哪些点属于一个连通分量呢? 那就是通过并查集了. 这部分并不难, 就略过了.

最后, 上代码

class Solution
{
  vector<vector<bool>> grid;
  queue<int> q;
  vector<int> flag;
  vector<bool> isTraversed;
  vector<int> fa;
  vector<int> ans;

public:
  int Find(int i)
  {
    if (fa[i] == i)
      return i;
    else
    {
      fa[i] = Find(fa[i]);
      return fa[i];
    }
  }
  void Union(int a, int b)
  {
    int fA = Find(a);
    int fB = Find(b);
    if (fA != fB)
    {
      fa[fA] = fB;
    }
  }
  int magnificentSets(int n, vector<vector<int>> &edges)
  {
    grid.resize(n + 1);
    for (int i = 0; i < n + 1; i++)
    {
      grid[i].assign(n + 1, false);
    }
    ans.resize(n + 1);
    fa.resize(n + 1);
    for (int i = 1; i <= n; i++)
    {
      fa[i] = i;
    }
    flag.assign(n + 1, -1);
    isTraversed.assign(n + 1, false);
    for (int i = 0; i < edges.size(); i++)
    {
      int u = edges[i][0];
      int v = edges[i][1];
      grid[u][v] = grid[v][u] = true;
      Union(u, v);
    }
    int ret = 0;
    // bfs + 染色 + 计数, 对每一个连通分量
    for (int i = 1; i <= n; i++)
    {
      isTraversed.assign(n + 1, false);
      flag.assign(n + 1, -1);
      if (!isTraversed[i])
      {
        isTraversed[i] = true;
        flag[i] = 0;
        int cnt = 0;
        // dfs
        q.push(i);
        while (!q.empty())
        {
          int cur = q.front();
          if (flag[cur] != ((cnt % 2) ^ 1))
            cnt++;
          q.pop();
          for (int i = 1; i <= n; i++)
          {
            if (grid[cur][i])
            {
              //如果之前没有染过色, 那么就进行染色
              if (flag[i] == -1)
              {
                flag[i] = cnt % 2;
                // cout << i << " " << cnt << endl;
                q.push(i);
                isTraversed[i] = true;
              }
              //如果之前已经染过色, 那么判断颜色是否正确
              else
              {
                if (flag[i] != cnt % 2)
                  return -1;
              }
            }
          }
        }
        ans[i] = cnt;
      }
    }
    for (int i = 1; i <= n; i++)
    {
      Find(i);
    }
    map<int, int> mp;
    for (int i = 1; i <= n; i++)
    {
      int idx = fa[i];
      if (mp.find(idx) == mp.end())
      {
        mp[idx] = ans[i];
      }
      else
      {
        if (ans[i] > mp[idx])
          mp[idx] = ans[i];
      }
    }
    for (auto it = mp.begin(); it != mp.end(); it++)
    {
      ret += it->second;
    }
    return ret;
  }
};

class Solution
{
  vector<vector<int>> grid;
  queue<int> q;
  vector<int> flag;
  vector<int> fa;
  vector<int> ans;

public:
  int Find(int i)
  {
    if (fa[i] == i)
      return i;
    else
    {
      fa[i] = Find(fa[i]);
      return fa[i];
    }
  }
  void Union(int a, int b)
  {
    int fA = Find(a);
    int fB = Find(b);
    if (fA != fB)
    {
      fa[fA] = fB;
    }
  }
  int magnificentSets(int n, vector<vector<int>> &edges)
  {
    grid.resize(n + 1);
    ans.resize(n + 1);
    fa.resize(n + 1);
    for (int i = 1; i <= n; i++)
    {
      fa[i] = i;
    }
    flag.assign(n + 1, -1);
    for (int i = 0; i < edges.size(); i++)
    {
      int u = edges[i][0];
      int v = edges[i][1];
      grid[u].push_back(v);
      grid[v].push_back(u);
      Union(u, v);
    }
    int ret = 0;
    // bfs + 染色 + 计数, 对每一个连通分量
    for (int i = 1; i <= n; i++)
    {
      flag.assign(n + 1, -1);
      flag[i] = 0;
      int cnt = 0;
      // bfs
      q.push(i);
      while (!q.empty())
      {
        int cur = q.front();
        if (flag[cur] != ((cnt % 2) ^ 1)) cnt++;
        q.pop();
        for (int j = 0; j < grid[cur].size(); j++)
        {
          {
            //如果之前没有染过色, 那么就进行染色
            if (flag[grid[cur][j]] == -1)
            {
              flag[grid[cur][j]] = cnt % 2;
              q.push(grid[cur][j]);
            }
            //如果之前已经染过色, 那么判断颜色是否正确
            else
            {
              if (flag[grid[cur][j]] != cnt % 2)
                return -1;
            }
          }
        }
      }
      ans[i] = cnt;
    }
    map<int, int> mp;
    for(int i = 1; i <= n; i++) {
        Find(i);
    }
    for (int i = 1; i <= n; i++)
    {
      int idx = fa[i];
      if (mp.find(idx) == mp.end())
      {
        mp[idx] = ans[i];
      }
      else
      {
        if (ans[i] > mp[idx])
          mp[idx] = ans[i];
      }
    }
    for (auto it = mp.begin(); it != mp.end(); it++)
    {
      ret += it->second;
    }
    return ret;
  }
};

0x18 力扣第328周周赛T4 最大价值和最小价值和的差值

  • 题目分析

首先注意到题目数据中price[i] >= 1, 这个条件大大简化了题目的要求, 因为对于任何节点开始的最小价值路径, 必然就是当前的根节点, 而再增加任意节点都会使路径和增加, 这样的话, 最大价值路径-最小价值路径=当前节点的所有子节点为起点的、不经过当前节点的最大价值路径。

之所以要强调**不能经过当前节点**, 是为了避免搜索的过程中发生重复遍历, 即a->b->a这种情况, 也就是要求不能访问已经访问过的节点. 这里可以通过一个vis[]数组来保存已经访问过的节点, 也可以利用树的性质: 树中一条路径上, 当前节点除了与其父节点直接相连, 不会与其任何祖先相连, 否则就会出现环. 这样一来, 我们只需要在dfs的时候记录当前节点的父节点, 避免重复访问父节点即可.

  • 解题思路

现在, 我们先不考虑数据规模, 看看如何求解对于一个特定顶点为根的最大开销. 根据之前的分析, 也就是求解**根节点所连子节点的最大路径的最大值(不能经过根节点). 然后, 就会发现这里存在一个关系的递推: 根节点所连子节点为起点的最大路径值=这个子节点的price+该子节点的子节点的最大路径值.我们发现这个递归关系的两个量都是只关于当前节点的值, 也就是说, 可以通过记忆化**每个节点的所有子节点为起点的最大路径值, 来避免重复计算. 当完成了所有的记忆化工作后, 取之中的最大值, 就是答案.

定义函数int dfs(int cur, int fa), 该函数求解并返回以当前节点为起点的且不经过其父亲节点的路径中的最大值, 不难发现每一次这样的函数访问就对应了图中的一条有向边.

最后, 我们注意到, 由于在单次dfs的过程中不允许重复访问, 这导致对于每一个访问到的子节点, 是不会求解以其父节点为起点的最大路径值的, 这就导致单次dfs并不能完成全部的记忆化. 不过好在记忆化避免了重复计算, 每一条边对应的dfs(cur, fa)只会访问一次, 因此不妨对每个顶点做一次dfs(cur, -1), 并在过程中更新最大值, 最后返回即可.

  • 复杂度分析

  • 建立邻接表的复杂度为O(V) = O(N),

  • 由于记忆化的原因, dfs只会被调用O(V) = O(N)次.

因此总体的时间复杂度为O(N).

空间复杂度为O(N).

AC代码 
class Solution {
  vector<vector<long long int>> v;//每一个顶点以某个点为起点的最大路径和
  vector<vector<int>> adj;//邻接表
  vector<int> price;
  long long ans = 0;
  long long int dfs(int cur, int fa) {
    //得到该点下面的所有节点的路径和
    long long int ret = 0;
    for(int i = 0; i < adj[cur].size(); i++) {
      int to = adj[cur][i];
      if(v[cur][i] == 0 && to != fa) {
        v[cur][i] = dfs(to, cur);
      }
      if(to != fa && v[cur][i] > ret) ret = v[cur][i];
      if(v[cur][i] > ans) ans = v[cur][i]; 
    }
    return ret + price[cur];
  }
public:
    long long maxOutput(int n, vector<vector<int>>& edges, vector<int>& price) {
      adj.resize(n);
      v.resize(n);
      this->price = price;
      for(auto edge : edges) {
        int u = edge[0];
        int v = edge[1];
        adj[u].push_back(v);
        adj[v].push_back(u);
      }
      for(int i = 0; i < n; i++) {
        v[i].assign(adj[i].size(), 0);
      }
      for(int i = 0; i < n; i++) {
        dfs(i, -1);
      }
      return ans;
    } 
};

戳啦, 被Hack了😥

经网友指正, 这个算法的复杂度分析的有问题, 在对于星状图这样的情况下, 时间复杂度会达到O(N^2). 可能正解还是需要用到什么"换根dp"吧.

0x19 力扣第328周周赛T2 子矩阵元素加1

强烈推荐

为数不多的做不出来的T2. 纯技巧, 不会就是做不出来. 虽然笔者接触过二维差分, 但是还是理解不够, 做题时想到了这个idea, 但是觉得没啥用, 没有想到具体细节.

贴一篇答案

class Solution {
public:
    vector<vector<int>> rangeAddQueries(int n, vector<vector<int>>& queries) {
        // 计算差分数组
        int f[n + 2][n + 2];
        memset(f, 0, sizeof(f));
        for (auto &qry : queries) {
            int r1 = qry[0], c1 = qry[1], r2 = qry[2], c2 = qry[3];
            f[r1][c1]++; f[r2 + 1][c2 + 1]++;
            f[r1][c2 + 1]--; f[r2 + 1][c1]--;
        }

        // 差分数组的二维前缀和就是答案
        vector<vector<int>> ans(n, vector<int>(n));
        for (int i = 0; i < n; i++) for (int j = 0; j < n; j++) ans[i][j] = f[i][j];
        for (int i = 0; i < n; i++) for (int j = 1; j < n; j++) ans[i][j] += ans[i][j - 1];
        for (int i = 1; i < n; i++) for (int j = 0; j < n; j++) ans[i][j] += ans[i - 1][j];
        return ans;
    }
};

作者：tsreaper
链接：https://leetcode.cn/problems/increment-submatrices-by-one/solution/by-tsreaper-mqla/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

0x1a 力扣第330场周赛T4 统计上升四元组

  • 题目分析

先来看O(n^3)的做法.

笔者首先是做了一个预处理: 求出每个元素idx左右两边pos位置开始到该元素为止,大于nums[idx]的数的个数. 用int cnt[idx][pos]来存储. 显然, 这可以在O(n^2)的时间内完全求解.

首先, 枚举i, k, 这样就是要寻找(i, k)对应的(j, l)对数. 其中,

  • i < j < k \wedge nums[i] < nums[k] < nums[j] , 相当于求"i,k之间大于nums[k]的元素个数", 这个值等于cnt[k][0] - cnt[k][i].
  • l > k \wedge nums[j] < nums[l], 这个值等于cnt[j][n-1] - cnt[j][k].

看起来, 经过预处理后, 就能以O(1)的时间来得到(j, l), 但是笔者具体实现以后, 才发现: l是关于j的函数, 因此需要确定j, 才能确定l. 这就意味着需要再遍历一遍j, 然后逐次累加l的种数. 这样下来, 复杂度达到O(n^3), 结果确实是TLE.

看来, 似乎是预处理得还不够, 还有没有能够进一步预处理的呢?

刚才因为不断地迭代j并累加cnt[j][n-1] - cnt[j][k]导致复杂度升高, 能不能把这个过程拿到枚举i, k的循环之外, 先进行运算呢?

既然在确定了j, k以后, 可以通过O(1)时间得到l的个数, 因为\displaystyle \sum_{j, l}(j, l) = \sum_j \sum_l (j, l), 那么就可以通过枚举j, k, 并累加得到任意i, k对应的(j,l)对数. 这个预处理的复杂度同样是O(n^2). 代码中, 用int c[j][k]来表示在[j, k-1]区间内所有能取到的j对应的l的数量之和, 也就是i = j-1, k=k情况下的(j ,l)对的数目.

总的来说, 经过两次O(n^2)的预处理后, 只需要以O(n^2)枚举(i, k), 就能以O(1)的时间复杂度得到对应的(j ,l)对的数目.因此总的时间复杂度也顺利降至O(n^2).

最后, 也是比较坑的地方, 由于C++限制, 如果将两个数组开在类里面会爆栈, 所以必须作为全局变量来存储.

教训

第一次遇到因为数组开大导致爆栈RE的, 傻傻的我找了半天也没找到RE的原因, 遗憾没能AC.

AC 
int cnt[4005][4005]; //cnt[idx][pos]从pos开始到idx为止大于nums[idx]的个数
int c[4005][4005];
class Solution {
  vector<int>nums;
  void get_cnt(int idx) {
    cnt[idx][idx] = 0;
    //向左边
    int l = idx - 1;
    while(l >= 0) {
      if(nums[l] > nums[idx]) cnt[idx][l] = cnt[idx][l+1] + 1;
      else cnt[idx][l] = cnt[idx][l+1];
      l--;
    }
    //向右边
    int r = idx+1;
    int n = this->nums.size();
    while(r < n) {
      if(nums[r] > nums[idx]) cnt[idx][r] = cnt[idx][r-1] + 1;
      else cnt[idx][r] = cnt[idx][r-1];
      r++;
    }
  }
  //枚举j, 统计[j, k-1]间所有的(j, l)对的数目.
  void func(int k) {
    int j = k - 1;
    c[k][k] = 0;
    int n = nums.size();
    while(j >= 0) {
      if(nums[j] > nums[k]) c[k][j] = c[k][j+1] + (cnt[j][n-1] - cnt[j][k]); 
      else c[k][j] = c[k][j+1];
      j--;
    }
  }
public:
    long long countQuadruplets(vector<int>& nums) {
      this->nums = nums;
      int n = nums.size();
      for(int i = 0; i < n; i++) {
        get_cnt(i);
      }
      for(int i = 0; i < n-1; i++) {
        func(i);
      }
      long long ret = 0;
      for(int i = 0; i < n-1; i++) {
        for(int j = i+2; j < n-1; j++) {
          if(nums[j] < nums[i]) continue;
          ret += c[j][i+1];
        }
      }
      return ret;
    }
};

0x1b 力扣第331场周赛T3 打家劫舍IV

  • 题目信息

详见网站

  • 题目分析

从题目也能预感到, 应该是一道dp / 贪心 题. 但是与经验中的题目不同, 这道题的数据范围是比较大的, 首先n~10^5, 其次k~10^5, 如果直接dp的话, 连空间都不够.

笔者在比赛的时候是以dp的角度来分析(主要是没想到别的方法), 先写状态转移方程: 定义状态函数f(idx, k), 意思是从0到idx未知, 选择k个元素的最大值的最小值. 显然, f(nums.size-1, k)就是答案. 该函数具有如下的转移关系:

f(idx, k) = \min {\begin{cases}f(idx - 1, k),\quad idx > 0 \\ \max\{f(idx - 2, k-1) , nums[idx]\}, \quad idx > 1 \end{cases}}

注意, 实际上, 由于要求不能连续抢劫, 因此任意f(idx, k)都满足idx \ge 2(k-1), 否则, 该状态是无意义的.

由上式发现该状态函数只受到k, k-1的影响, 因此在空间上没必要时刻存储所有的k, 可以开两个大小为n的数组, 分别存k, k-1即可.

解决的空间上的问题, 时间上的问题似乎不好处理. 笔者最终只写出了O(nk)的算法, 结果显然TLE, 卒😞.

  • 正解: 二分 + 贪心

有时候换个角度, 问题就会简单许多

怎么降低复杂度? 要么是发现更快的转移方程, 要么就得考虑换个方法了.

笔者做题时考虑过贪心, 也许也考虑过二分, 但是都没有仔细想下去.

看来二分答案的思路还是需要巩固啊.

一旦能想到对窃取能力进行二分, 然后每次只需要判断能够达到该窃取能力即可. 这种思路已经多次出现了, 将一个寻找最大值的问题转化为了判定某个值能否达到的问题 . 当然, 能够二分的一个关键的前提是窃取能力是一个"向上包含"的变量, 即, 如果窃取能力能取到x, 则k以上的就一定也能取到, 如果x取不到, 则x以下也一定取不到.

那么, 子问题就是, 对于给定的窃取能力x, 问数组中能够取到k个不超过x且不相邻的元素. 这个问题可以用dp解决, 也可以用贪心解决, 因为, 满足了就选, 得到的个数一定不小于其他选法.

贴一份答案吧 
class Solution {
public:
    int minCapability(vector<int>& nums, int K) {
        int n = nums.size();

        // 检查二分的答案 X 是否合法
        auto check = [&](int X) {
            int cnt = 0;
            // 从左到右枚举每座房子，能抢就抢
            // j 是上一次抢夺的下标
            for (int i = 0, j = -2; i < n; i++) if (nums[i] <= X && i - j > 1) {
                cnt++;
                j = i;
            }
            return cnt >= K;
        };

        int head = nums[0], tail = nums[0];
        for (int x : nums) {
            head = min(head, x);
            tail = max(tail, x);
        }

        // 二分答案
        while (head < tail) {
            int mid = (head + tail) >> 1;
            if (check(mid)) tail = mid;
            else head = mid + 1;
        }
        return head;
    }
};

// 作者：TsReaper
// 链接：https://leetcode.cn/circle/discuss/2Gdn7F/view/ZdFGaW/
// 来源：力扣（LeetCode）
// 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

0x1c AcWing 4805.加减乘

这是一道AcWing网站上的周赛题, 笔者第一次在该网站刷题, 随便挑了一道周赛hard, 就不会写🤣. 果然, dp还是不熟悉, 这道题要分析的数学部分比较多, 基本上是一道数学题.

初来乍到, 先跟yxc学一招. https://www.acwing.com/video/4613/

0x1d DSOJ W14T2 小蓝鲸游园计划

  • 题目信息

  • 题目分析

本题的难度主要在于注意到度数大于\sqrt{m}的顶点的数量级不超过\sqrt{m}个, 因此对这部分的顶点进行边枚举, 然后更新, 总的时间复杂度不超过m\sqrt{m}.

对于度数小于\sqrt{m}的顶点, 直接枚举所有的点, 这部分的时间复杂度不超过mn.

对数据进行分部, 分别采用不同的解法, 以降低总体的时间复杂度, 这个方法是不容易想到的.

AC 
#include <bits/stdc++.h>

using namespace std;

int n;
int m;
int *val;
vector<vector<int>> adList;

int ret = 0;
set<pair<int, int>> st;

int cntVal(int u1, int v1, int u2, int v2)
{
  if (u1 == -1 && v1 == -1)
  {
    if (u2 == -1 && v2 == -1)
      return 0;
    else
      return val[u2] + val[v2];
  }
  else if (u2 == -1 && v2 == -1)
    return val[u1] + val[v1];
  else
  {
    int sum = val[u1] + val[v1] + val[u2] + val[v2];
    if (u1 == u2)
      sum -= val[u1];
    if (u1 == v2)
      sum -= val[u1];
    if (v1 == u2)
      sum -= val[v1];
    if (v1 == v2)
      sum -= val[v1];
    return sum;
  }
}

// 对于度数小于sqrt m的点, 枚举两个相邻的点, 查看能不能构成三角形,  如果能, 就更新答案
int solve1(int idx)
{
  int sum = 0;
  int u1 = -1, v1 = -1, u2 = -1, v2 = -1;
  for (int k = 0; k < 2; k++)
  {
    for (int i = 0; i < adList[idx].size(); i++)
    {
      for (int j = i + 1; j < adList[idx].size(); j++)
      {
        int u = adList[idx][i];
        int v = adList[idx][j];
        if (st.find({u, v}) != st.end())
        {
          // update
          int val1 = cntVal(u1, v1, u, v);
          int val2 = cntVal(u, v, u2, v2);
          if (u1 != -1 && u2 == -1 && val1 == val2)
          {
            sum = val1;
            u2 = u;
            v2 = v;
          }
          else if (val1 > val2)
          {
            if (val1 > sum)
            {
              u2 = u;
              v2 = v;
              sum = val1;
            }
          }
          else
          {
            if (val2 > sum)
            {
              u1 = u;
              v1 = v;
              sum = val2;
            }
          }
        }
      }
    }
  }
  if (u1 == -1 || u2 == -1)
    return 0;
  else
    return sum + val[idx];
}
// 对于度数大于sqrt m的点, 这样的点数量不超过sqrt m两级, 通过枚举所有边的方式, 进行更新
int solve2(int idx)
{
  int sum = 0;
  int u1 = -1, v1 = -1, u2 = -1, v2 = -1;
  for (int k = 0; k < 2; k++)
  {
    for (auto it = st.begin(); it != st.end(); it++)
    {
      int u = it->first;
      int v = it->second;
      if (u < v)
        continue;
      // 这条边不能包含idx
      if (idx == u || idx == v)
        continue;
      if (st.find({u, idx}) != st.end() && st.find({v, idx}) != st.end())
      {
        // update
        int val1 = cntVal(u1, v1, u, v);
        int val2 = cntVal(u, v, u2, v2);
        if (u1 != -1 && u2 == -1 && val1 == val2)
        {
          sum = val1;
          u2 = u;
          v2 = v;
        }
        else if (val1 > val2)
        {
          if (val1 > sum)
          {
            u2 = u;
            v2 = v;
            sum = val1;
          }
        }
        else
        {
          if (val2 > sum)
          {
            u1 = u;
            v1 = v;
            sum = val2;
          }
        }
      }
    }
  }
  if (u1 == -1 || u2 == -1)
    return 0;
  else
    return sum + val[idx];
}

int main()
{
  scanf("%d %d", &n, &m);
  val = new int[n];
  adList.resize(n);
  for (int i = 0; i < n; i++)
  {
    scanf("%d", &val[i]);
  }
  for (int i = 0; i < m; i++)
  {
    int cur = 0;
    int u, v;
    scanf("%d %d", &u, &v);
    st.insert({u, v});
    st.insert({v, u});
    adList[u].push_back(v);
    adList[v].push_back(u);
  }
  for (int i = 0; i < n; i++)
  {
    int cur = 0;
    if (adList[i].size() < sqrt(m))
    {
      cur = solve1(i);
    }
    else
    {
      cur = solve2(i);
    }
    if (cur > ret)
      ret = cur;
  }
  printf("%d", ret);
  return 0;
}

0x1e DSOJ W15T3 小蓝鲸返乡

  • 题目信息

  • 题目分析

考察对floyd算法思想的理解, 关键是"尝试松弛", 因此路径的数量与距离一样是可以维护的.

AC 
#include<bits/stdc++.h>

using namespace std;

#define MOD 1000000007

int n;
int m;
long long **dis;
long long **cnt;

const int inf = 0x7fffffff;


void floyd() {
  for(int k = 0; k < n; ++k) {
    for(int i = 0; i < n; ++i) {
      if(dis[i][k] == inf) continue;
      for(int j = i+1; j < n; ++j) {
        if(dis[k][j] == inf) continue;
        if(dis[i][j] < dis[i][k] + dis[k][j]) continue;
        if(dis[i][j] > dis[i][k] + dis[k][j]) {
          cnt[i][j] = ((cnt[i][k] % MOD) * (cnt[k][j] % MOD)) % MOD;
        }
        else if(dis[i][j] == dis[i][k] + dis[k][j]) {
          cnt[i][j] += ((cnt[i][k] % MOD) * (cnt[k][j] % MOD)) % MOD;
        }
        cnt[j][i] = cnt[i][j];
        dis[i][j] = dis[j][i] = dis[i][k] + dis[k][j];
      }
    }
  }
}

int main() {
  scanf("%d %d", &n, &m);
  dis = new long long*[n];
  cnt = new long long*[n];
  for(int i = 0; i < n; i++) {
    dis[i] = new long long[n];
    cnt[i] = new long long[n];
    for(int j = 0; j < n; j++) {
      dis[i][j] = inf;
      cnt[i][j] = 0;
    }
  }
  for(int i = 0; i < m; i++) {
    int u, v, val;
    scanf("%d %d %d", &u, &v, &val);
    dis[u][v] = dis[v][u] = val;
    cnt[u][v] = cnt[v][u] = 1;
  }
  floyd();
  printf("%d", cnt[0][n-1] % MOD);
  return 0;
}

0x1f 数据结构大作业 4题

四道题都挺有意思的, 具有一定的挑战性. 作为作业, 这几题的思路&解法见作业报告

0x20 力扣第336场周赛T3 统计美丽子数组

最近水平下滑太明显了, 将近一个月的缺乏训练, 连续三场周赛掉分😥, 要开始努力了

  • 题目分析

直接暴力的话, 时间复杂度是O(n^3), 如果进行一些预处理的话, 时间复杂度也许可以降到O(n^2), 但是还是不够, 如果能过的话, 时间复杂度应该要到O(n\log n)或者O(n), 这个地方笔者在思考的时候陷入了滑窗和DP的困境: 如果要满足复杂度, 那就意味着不能多次遍历, 但是似乎并没有这样的算法能够在一遍遍历后就统计出结果.

赛后来看, 异或, 前缀和, 这两者都不陌生, 但是能够结合起来运用, 还是头一回见. 这道题对异或的性质的考察是很好的.

异或前缀和 
class Solution:
def beautifulSubarrays(self, nums: List[int]) -> int:
    ans = s = 0
    cnt = Counter({s: 1})  # s[0]
    for x in nums:
        s ^= x
        ans += cnt[s]
        cnt[s] += 1
    return ans

0x21 ACW T96 奇怪的汉诺塔

  • 题目分析

3根柱子的Hanoi问题是经典的, 本题做了一个小的变式, 4根柱子会如何?

笔者第一遍做的时候犯的一个错误是: 先把n-2移动到B, 然后把第n-1移到C, 把第n移到D, 然后再移过来, 因此得到的状态转移方程T(n) = 2 \times T(n-2) + 3, 然后代入了一个3, 似乎没问题, 于是就挂了.

其实这么想是没什么道理的. 这个推广其实也考察了对状态的理解. 因为汉诺塔要求大盘子要在小盘子下面, 因此第一次可以选取k个盘子移动到B上, 这个过程是可以用到4根柱子的, 但是剩下来的n-k个盘子就只能在3根柱子上移动, 这个状态是和第一次不同的, 因此状态转移方程为Q(n) = 2 \times Q(k) + T(n-k), 其中Q代表可以用四根柱子, T代表3根, 那么k选什么呢? 就需要遍历所有可能的k, 取结果的最小值.

进一步思考

这题其实还有一些值得思考的地方: 为什么3->4, 就不再是划分成1, n-1来移动呢? 可能的原因在于, 原先3根柱子的时候, 第一次移动以后, 第二次只能用2根柱子, 而从一根柱子上移动到另一根上, 如果盘子数多于1个, 就无法完成了. 因此我们分析经典汉诺塔问题时, 总是先考虑移动上n-1块, 然后在只剩两根"可以周转"的柱子, 于是只能移动最下面的那一块了. 到了4根柱子的时候, 第一次移动完, 还有3根柱子, 这个问题就完全等同于经典汉诺塔问题, 因此这时候将n划分成k, n-k, 这个k的取值就不唯一了. 因此需要取最小值(如果通过数学上证明有最优划分, 那么这个过程可以简化).