离散数学课堂笔记¶

命题逻辑¶

程序分析时需要考虑布尔表达式的可满足性
程序验证有关表达式逻辑推理
布尔运算符
与
或
非
命题陈述句 i.e.陈述事实的句子
原子命题与复合命题
命题表达式
命题变元
运算符：
否定
合取
析取
蕴含
双（向）蕴含
运算符的优先级：! > && > || > -> > <->
命题的真值表
成真指派
成假指派
永真式、矛盾式
逻辑等价

iff 对任意的变元赋值，两个命题取值总是相同

两个命题构成的双向蕴含命题为永真

双重否定律
幂等律
交换律
结合律
分配律
德摩根律
吸收律
支配律
恒等律
排中律 $a\vee \neg a\iff 1$
矛盾律
蕴含恒等式 $a\to b\iff \neg a \vee b$
假言易位i.e.逆否命题 $a\to b \iff \neg b\to \neg a$
归谬论

语义蕴含¶

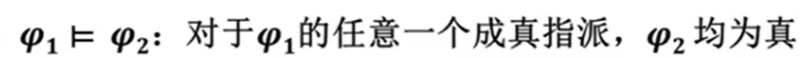
可以构造一个复合命题，说明其为永真的。

逻辑等价：双向蕴含的命题永真

可满足性：存在一组成真指派

命题逻辑的判定性¶

是否有通用的算法，判定命题是否永真？

命题的合取范式(Conjunctive normal form) CNF

判断命题是否永真

命题的析取范式(Disjunctive nromal form)

DNF

求解命题的所有成真指派

命题逻辑的自然演绎规则¶

假言推理（A推B，且A，则B）

取拒式（A推出B,且非B,那么非A）

假言三段论（A推出B， B推出C，则A推出C）

析取三段论（要么A要么B，且不是A，则B）

附加律(or一个别的东西)

化简律（取其中一个）

合取律（两个命题连接）

消解律（A或B，　非A或C，则或C）

谓词逻辑初步¶

谓词（Predicate）¶

真值依赖于x的取值
论域(domain of discourse)：变量x的取值范围

逻辑公式（Formula）¶

原子陈述是逻辑公式
若P是逻辑公式，x是自由变量，则对于所有的x/存在x，满足P 也是逻辑公式
若P和Q是逻辑公式，则非并交蕴含都是逻辑公式
$<span class="arithmatex"><span class="MathJax_Preview">注意</span><script type="math/tex">注意$ ：量词的优先级高于其他逻辑运算符
计算机编程：解析树

量化公式的变元¶

约束变元：作用域受限或者被赋值的变量
自由变元：

量化公式的真假¶

多个量词并用交换全称和存在性量词，命题不一定一样

论域的无限性，加深了推理的困难。

常用逻辑等价式¶

非所有 = 存在非
非存在 = 所有非

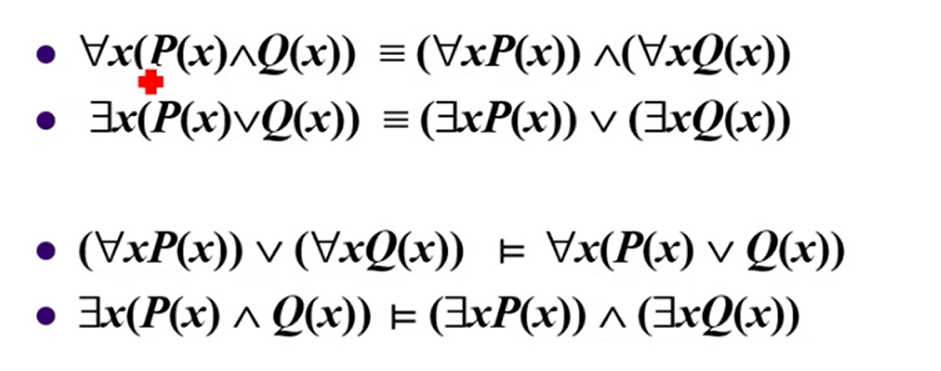
注意：下面两种情形是单项蕴含！！

全称/存在量词中与变量无关的命题可以提出

注意：下面两种情形的量词会发生改变！（运用量词的德摩根律）

主析取/合取范式¶

析取范式
合取范式

前束范式（Prenex Normal Form）¶

前束析取范式（PDNF）¶

前束合取范式（PCNF）¶

基于规则的推理¶

一阶谓词逻辑FOL的一些定论¶

自然演绎规则（含量词相关的）是正确的、完备的。
不可判定的：

证明方法¶

证明过程¶

直接法¶

反证法： p -> q == ~q -> ~p¶

归谬法：q == ~q -> F¶

分情形证明¶

集合及其运算¶

集合的定义¶

无序确定
definite distinct objects
朴素集合论 naive set theory

集合的描述¶

文氏图的局限性：四个以上集合的关系表示困难

集合相等¶

集合A中的元素在B中，反之亦然（定义）
A包含于B，反之亦然（定理）

集合的包含关系¶

$A \subseteq B$ 表示集合A包含于集合 $\mathrm{B}$ ，等价于A的元素都是 $\mathrm{B}$ 的元素，也就是 $$ (x \in A \Rightarrow x \in B) \Leftrightarrow A \subseteq B $$ $A \subset B$ 表示集合A真包含于集合 $\mathrm{B}$ ，等价于 $\mathrm{A}$ 的元素都是 $\mathrm{B}$ 的元素并且 $\mathrm{B}$ 中元素一定比 $\mathrm{A}$ 多，排除了相等的情况，也就是 $(x \in A \Rightarrow x \in B \wedge A \neq B) \Leftrightarrow A \subset B$

集合的大小（势）//cardinality¶

card(X) or |X|
空集：
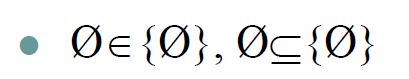
幂集：S是一个集合，**S的幂集**是S的==所有子集==的集合 //所有S的子集都是S的幂集的元素
推论：
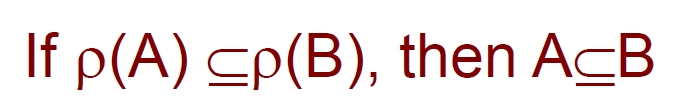
反之亦然

相对补¶

A - B == B对A的补集
U - B == ~B //B的补集

对称差¶

异或

广义并广义交¶

广义并
A的层次比U A 高一级 //A是集合的集合， U A是集合的元素的元素的集合，故UA与A的子集是同层次的
广义交
注意:限制条件是A非空, 否则无意义( $<span class="arithmatex"><span class="MathJax_Preview">y \in A</span><script type="math/tex">y \in A$ 为假)

皮亚诺公理(Peano axioms for natural numbers)¶

利用集合的关系来表示自然数

构造后继: n -> n+1 : A -> A U {A}
比大小: $$3 \cup 2 $$ == max(3, 2)
加法

Russel paradox¶

理发师悖论

ZFC公理（*）¶

笛卡尔乘积¶

有序偶¶

集合的笛卡尔乘积¶

集合相关命题的基本证明方式¶

核心思想：将==集合==的关系转换为==元素==的关系，从元素的角度来思考。
利用运算定义作逻辑等值式推演
集合 - 元素 - 集合
利用已知恒等式或等式作集合代数推演
跳过元素，直接利用结论
集合 - 集合
F == ~A $<span class="arithmatex"><span class="MathJax_Preview">\cap</span><script type="math/tex">\cap$ ~A T == A U～A
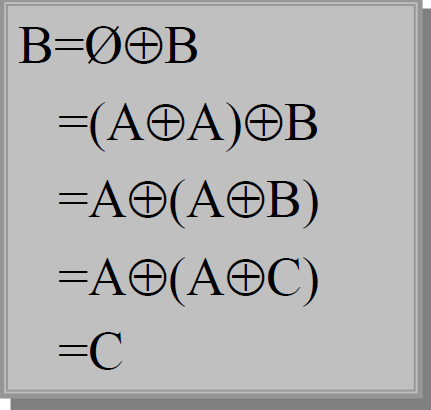
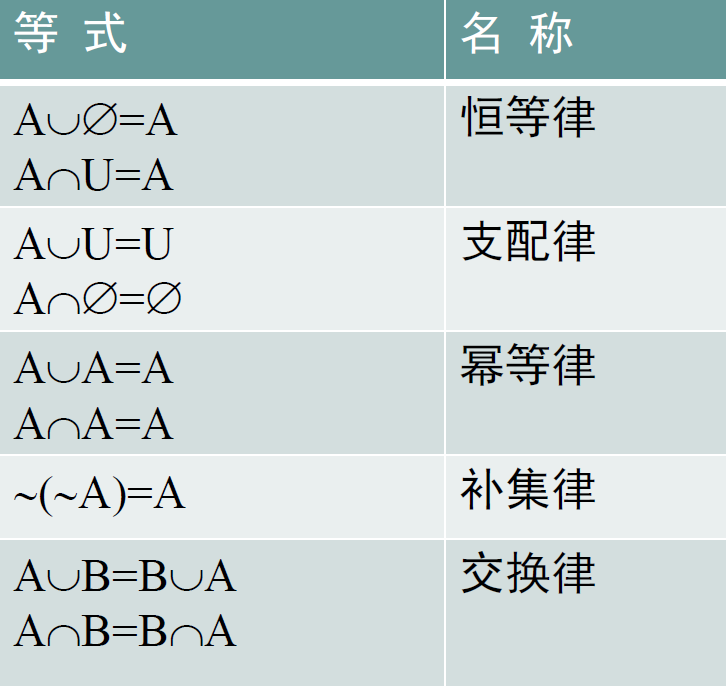
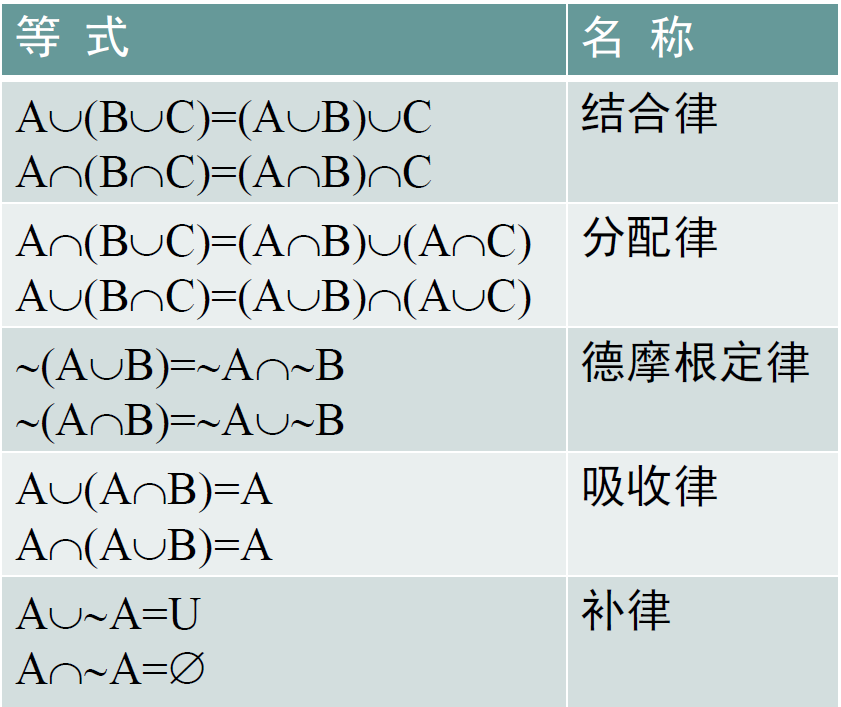
文氏图帮助推结论

关系及其运算¶

有序对（Ordered Pair）¶

次序的体现

笛卡尔乘积（Cartesian Product）¶

笛卡尔乘积也是集合

（二元）关系的定义¶

注意：关系一定要强调论域：**在XX上的**XX关系
笛卡尔积的一个子集
元素是有序对
笛卡尔积是全（域）关系
空集是空关系
**从A到B的**关系R（relation）； $<span class="arithmatex"><span class="MathJax_Preview">R \subseteq A \times B</span><script type="math/tex">R \subseteq A \times B$
若A==B，称为“**集合A上**的二元关系”
函数是一种特殊的关系

关系的表示¶

二元关系 -> 有向图

关系的运算¶

所有的集合运算都使用
逆运算
逆运算的复合类似矩阵的转置的复合
关系的复合
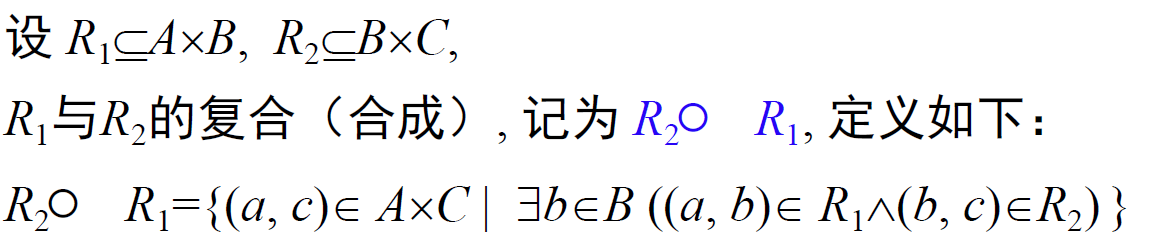
中间桥梁
注意：先后结合的顺序遵循就近原则

0-1矩阵运算¶

$A\cap B; A\cup B$
关系的迭代 == 矩阵的乘法
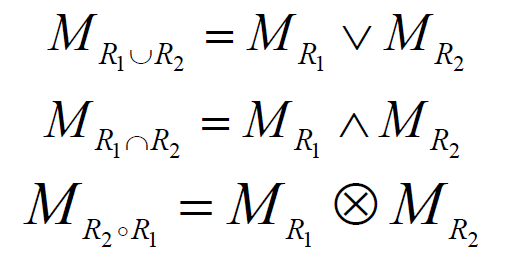
注意：0-1矩阵的运算符号、关系的运算符号

关系的性质¶

自反性（Reflexivity）¶

自反/ 反自反/ 既不是自反，又不是反自反

注意：反自反是一个比较强的概念，要求对于所有的元素都不具有自反性
有向图的表示：每一个节点都有环/每一个节点都没有环/有的有，有的没有
矩阵的表示：主对角线全1/主对角线全0/...
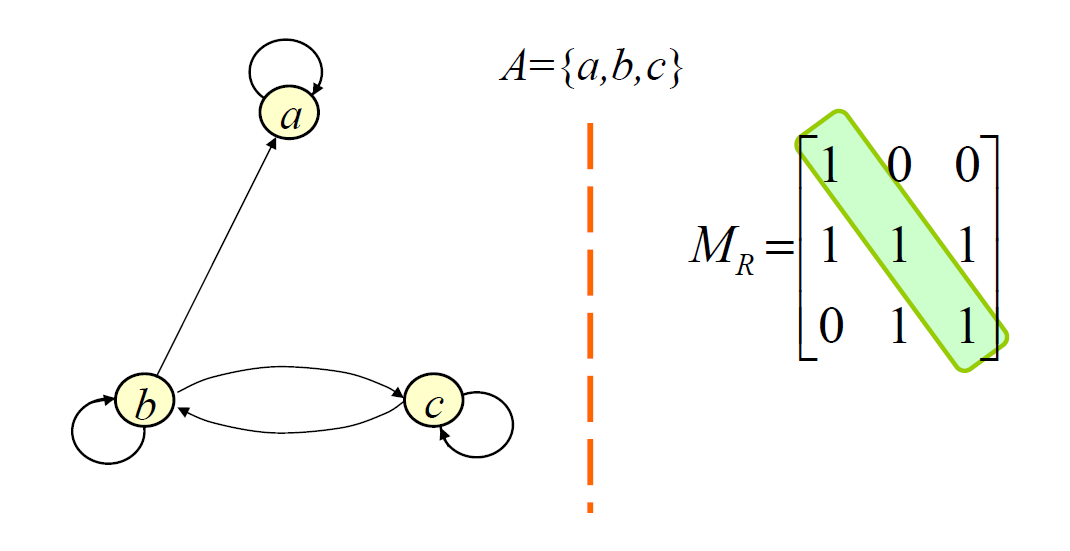
自反性判断的条件：一个关系具有自反性，当且仅当，恒等关系包含于该关系。

对称性（Symmetry）¶

对称的/ 反对称的（anti-）/ 既不是对称的，也不是反对称的 / 既是对称的，也是反对称的

反对称性：去除恒等关系后，不具有任何的对称关系。
有向图的表示：不同节点间的箭头数为0/2，对于节点是否有环不作要求 // 不同节点间的箭头数为0/1
空关系既是对称关系，也是反对称关系
对称关系与逆关系：¶

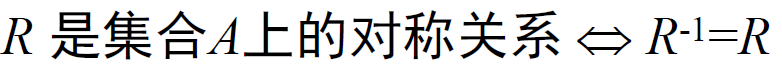传递性（Transitivity）¶

类似关系的复合
空关系是传递的

##### 传递性与==关系的乘幂==：

##### 关系的复合运算满足结合律

关系运算与性质的保持

	自反	反自反	对称	反对称	传递
R_(1)^(-1)	✓	✓	✓	✓	✓
R_(1)nnR_(2)	✓	✓	✓	✓	✓
R_(1)uuR_(2)	✓	✓	✓	x	x
R_(1)^(@)R_(2)	✓	x	x	x	x

函数及其运算¶

思考：若A有n个人元素，在A上的不同关系有多少个？

函数（function, mapping, transformation）的定义¶

Well defined(良定义)
函数的型构
象（image）、原象
定义域(domain)
值域(range)
伴域(codomain)

函数的集合¶

记 $\boldsymbol{B}^{A}$ 为 $A$ 到 $B$ 所有函数集合, 即 $\{\boldsymbol{F} \mid \boldsymbol{F}: \boldsymbol{A} \rightarrow \boldsymbol{B}\}$ , 读作 " $B$ 上 $A $"
A:定义域， B：陪域

命题: 设 $|A|=m,|B|=n$ , 则: $$ \left|B^{{A}\right|=|B|}=n^{m} $$

$$ f(\mathrm{X} \cap \mathrm{Y}) \subseteq f(\mathrm{X}) \cap f(\mathrm{Y}) $$

函数性质¶

单射（一对一）
injection, one-to-one function
$\forall x_1,x_2\in A, if \quad x_1 \neq x_2, then \quad f(x_1) \neq f(x_2)$
$\forall x_1, x_2, if \quad f(x_1) = f(x_2), then \quad x_1 = x_2$
满射（映上的）
surjection, onto function
$\forall y \in B, \exist x \in A ,s.t.\ f(x) = y$ ¶
双射
证明技巧：利用单射/满射 + 集合的基数+反证来证明（鸽笼原理）

$$1 - 1 function : |A| \leq |B| \ onto function: |A| \geq |B| $$

函数的复合¶

- 单射（单射） == 单射
- 满射（满射） == 满射
- 对于加法、乘法是封闭的

问题：若 $f \circ g$ 是满射, 能推出 $f$ 和 $g$ 是满射吗?
$f$ 一定是满射, $g$ 不一定是满射。若 $f \circ g$ 是单射, 能推出 $f$ 和 $g$ 是单射吗?
$g$ 一定是单射, $f$ 不一定是单射。

集合的基数¶

集合的等势关系（ $A \approx B$ ）【找双射】¶

A， B中的元素可以找到一种方法，使得“一一对应”(1-1 function & onto function) [双射]

等势是等价关系

有限集与无限集¶

传统公理：整体大于部分

在无限集情况下不成立。

$S为无限集, iff.\ \exist S' \subseteq S,\ s.t. \ S'\approx S\\ i.e. 存在部分“等于”整体$
证明：类似希尔伯特旅馆问题。
自然数集是“最小的”无限集。
康托尔定理
任何集合与其幂集不等势.即: $A \approx \rho(A)$
证明要点: 设 $g$ 是从 $\mathrm{A}$ 到 $\rho(\mathrm{A})$ 的函数, 构造集合B如下: $\mathrm{B}=\{\mathrm{x} \mid \mathrm{x} \in \mathrm{A}$ , 但 $\mathrm{x} \notin g(\mathrm{x})\}$ 则 $\mathrm{B} \in \rho(\mathrm{A})$ , 但不可能存在 $\mathrm{x} \in \mathrm{A}$ , 能满足 $g(\mathrm{x})=\mathrm{B}$ , 因为, 如果有这样的 $x$ , 则 $x \in B$ iff. $x \notin B$ 。因此, $g$ 不可能是满射。
[没看懂。。。]
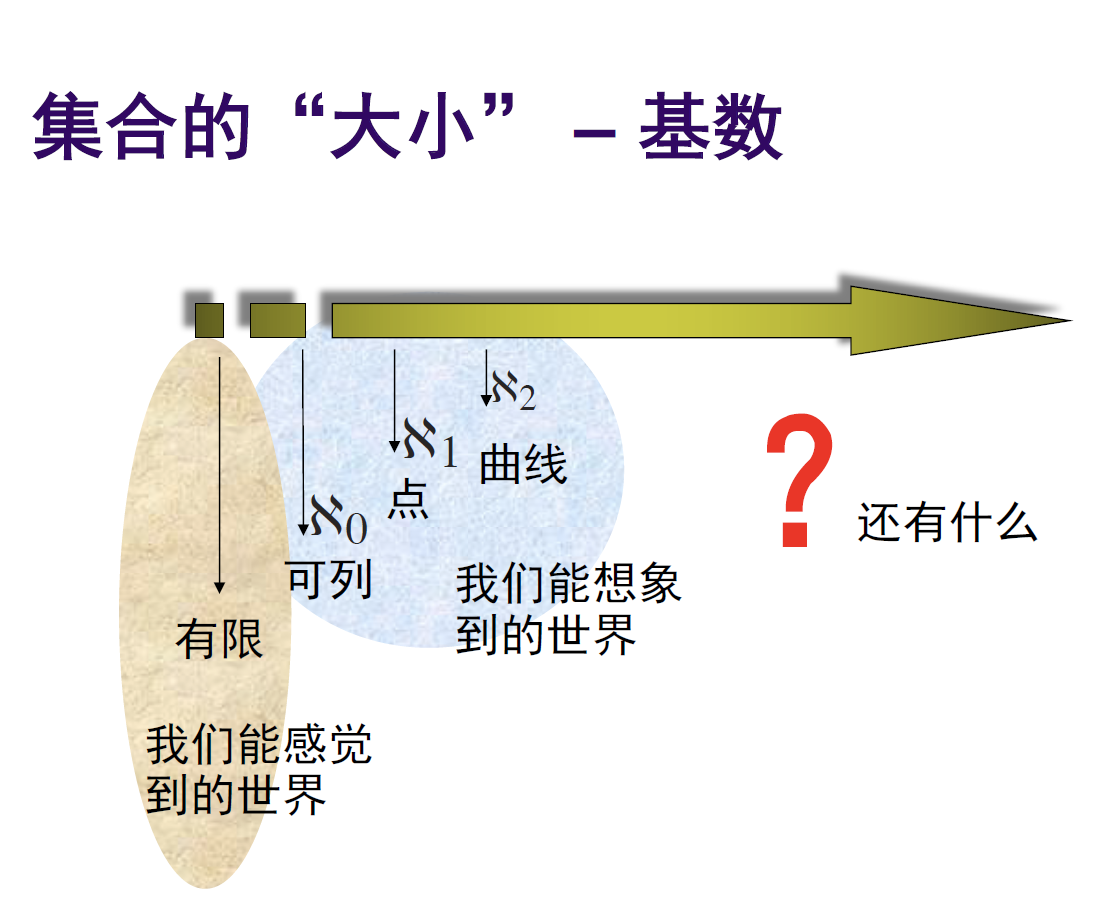
自然数集点集($$) 曲线
$\aleph_0\: \Z\ \Q\ \N\times \N\\ \aleph_1\: \R\ (0,1)\ [0,1] \\ \aleph_2$

可列集¶

直观概念：集合的元素可以按**确定的顺序**线性排列。确定的顺序，是指，对于序列中的任一元素，可以说出它“前一个”“后一个”元素是什么
自然数集的笛卡尔积为可列集
$l(m, n)=\frac{1}{2} \sum_{i=1}^{m+n} i+(m+1)=\frac{(m+n)(m+n+1)}{2}+(m+1)$
问题：三维的笛卡尔积的排列方式？
Cantor's diagonalization argument : to prove $\R$ is not a countable set

集合的优势关系（取代等势/三明治定理）¶

存在单射A-B, 则 B优势于A

自反性、反对称性、传递性-> 偏序集

真优势于（优势且不等势）

$\R$ 和 $\rho(\N)$ 等势¶

$[0,1) \approx\{0,1\}^{N}$ 从而 $R \approx \rho(N)$

注：右式可以视作一个由R映射到{0，1}的函数，也可以视作对R中元素的选择，即R的幂集；左式已经证明等势于R。

$[0,1)$ 中的数唯一地表示为 $0 . b_{1} \mathbf{b}_{2} b_{3} \mathbf{b}_{4} \cdots$ 不容许连续无数个 1 , 比如 $1 / 2=0.1000 \ldots$ (NOT 0.0111...)

$f:[0,1) \rightarrow\{0,1\}^{N}$ $\mathbf{0 .} \mathbf{b}_{1} \mathbf{b}_{2} \mathbf{b}_{3} \mathbf{b}_{4} \cdots \rightarrow \mathbf{b}_{1}, \mathbf{b}_{2}, \mathbf{b}_{3}, \mathbf{b}_{4} \cdots$ $f$ 是单射

注：这里小数是二进制的。即，任一个有唯一的二进制表示，二进制的第i位的0/1表示 $n_i$ 在/不在该集合中。

$g:\{0,1\}^{\mathrm{N}} \rightarrow[\mathbf{0}, 1)$ $\mathbf{b}_{1}, \mathbf{b}_{2}, \mathbf{b}_{3}, \mathbf{b}_{4} \ldots \rightarrow \mathbf{0 . b _ { 1 }} \mathbf{b}_{2} \mathbf{b}_{3} \mathbf{b}_{4} \ldots$ .//看做十进制数 $g$ 是单射

根据Bernstein定理, 得证

连续统假设¶

数论初步¶

整数¶

全序集无上界无下界

整除关系¶

可加性
可乘性
传递性

余数¶

模的基本性质: 令 $a, b \in \mathbb{Z}, d \in \mathbb{Z}^{+}$ , 则: $\circ(a+b) \bmod d=(a \bmod d+b \bmod d) \bmod d$ $\circ(a \times b) \bmod d=[(a \bmod d)(b \bmod d)] \bmod d$

$Pf. let a = q_1d + r. $

同余(a $\equiv$ b(mod k))¶

结论： $if\ p | q, then\ 2^p-1|2^q-1.\\ Pf.$

质数¶

prime number; not composite number
问题：
$\forall n \in \N, can\ we\ find\ n\ continuous\ composite\ numbers\ ?$
$Hint.\ let\ a_i= n ! + i$
命题：有无穷多质数。
$Pf.反证法。设所有的质数P_i,令n = \Pi P_i,利用贝祖定理，gcd(n,n+1) = 1,即n+1为质数$
质数定理：
设 $x \in \mathbb{R}^{+}, \pi(x)$ 为质数计数函数（i.e. 不大于 $x$ 的质数的个数）, 有 $$ \lim _{x \rightarrow \infty} \frac{\pi(x)}{x / \ln x}=1 $$
- 质数定理表明从不的概率约为 $1 / \ln n$ 质数的分布随着 $n$ 的增大逐渐稀疏孪生质数猜想（twin prime conjecture, Hilbert 1900）：
$\liminf _{n \rightarrow \infty}\left(p_{n+1}-p_{n}\right)=2 \\ 2013(张益唐): \liminf_{n\rightarrow \infty}\left(p_{n+1}-p_{n}\right) < 7 \times 10^7 \\ now: \liminf_{n\rightarrow \infty}\left(p_{n+1}-p_{n}\right) < 200^+$

基本算术定理¶

定理（算术基本定理）：每个大于 1 的整数皆可分解为有限个质数之积（这些质数称为质因子），若不考虑顺序, 则分解唯一 $\boldsymbol{n}=\boldsymbol{p}_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} \cdots p_{k}^{\alpha_{k}}\left(p_{1}<p_{2}<\cdots<p_{k}, \alpha_{i} \in \mathbb{Z}^{+}\right)$

$Pf. Hint. using\ lemma.1.$

裴蜀定理/贝祖定理（Bézout's identity）¶

$\forall a,b\in \Z^+, \exist s,t\in \Z s.t.\ gcd(a,b) = sa +tb$

$Pf.\ let \ x = minimun\ positive\ number\ that\ x = s'a+t'b\\let \ a= qx+r\\ let\ q = \lfloor {a\over x}\rfloor,r = a -xq, 0 \leq r < x\\ the n\ r = a - (s'a + t'b)q = (1-s')\cdot a + t'q\cdot b\\ then\ we\ find\ r\ is\ also\ the\ form\ r = sa + tb\\ but\ since\ x\ is\ the\ minimun\ one\ so\ r\ can\ only\ be\ 0.\\ \therefore q\ | {a\over x}, x| a, similarly, x|b, and\ x\ is\ the\ minimun\ one\\ so\ x = gcd(a,b).Q.E.D$

$lemma.1. p|ab\Rightarrow p|a \or p|b$

最大公约数¶

定理 (线性合成): 设 $a, b \in \mathbb{Z}^{+}$ , 则:

$(\exists s, t \in \mathbb{Z})(\operatorname{gcd}(a, b)=s a+t b)$

定理 (辗转相减): 设 $a, b \in \mathbb{Z}^{+}, a<b$ , 则:

$\operatorname{gcd}(a, b)=\operatorname{gcd}(a, b-a)$

定理 (辗转相除): 设 $a, b \in \mathbb{Z}^{+}, a>b$ , 则:

$\operatorname{gcd}(a, b)=\operatorname{gcd}(b, a \bmod b)$

中国剩余定理¶

欧拉函数¶

定义（欧拉函数）：对任意 $n \in \mathbb{Z}^{+}$ , $$ \varphi(n)=\left|\left{m \in \mathbb{Z}^{+} \mid m \leq n \wedge(m, n)=1\right}\right| $$ 例: $\varphi(3)=2, \varphi(4)=2, \varphi(12)=4$ 由容反原理 (末来课程详述) 可证 : $$ \varphi(n)=n \prod_{p \mid n}\left(1-\frac{1}{p}\right) $$ 其中 $\{p\}$ 为 $n$ 的所有质因子

$(m, n)=1 \rightarrow \varphi(m n)=\varphi(m) \varphi(n)$

$Pf.展开即可$
$example.\ (2,5) = 1, so\\ \ \varphi(2\times 5) = \varphi(10) = \varphi(2)\times \varphi(5) = |\{1\}|\times |\{1,2,3,4\}| = \varphi(10) = |\{1,3,7,9\}| = 4$

$p$ 为质数 $\rightarrow \varphi(p)=p-1$

定理 (Euler定理): 对 $a, n \in \mathbb{Z}^{+}$ , 若 $(a, n)=1$ , 则

$a^{\varphi(n)} \equiv 1(\bmod n)$

若上述 $n \in \mathbb{Z}^{+}$ 为质数, 由欧拉函数的性质易得到:

定理（Fermat小定理）：设正整数 $a$ 不是质数 $p$ 之倍数，则

$a^{p-1} \equiv 1(\bmod p)$

注：费马小定理是在欧拉定理基础上，将 $\varphi(n) \rightarrow \varphi(p),其中p为质数，故\varphi(p) = p-1$ 得到
例：求 $7^{222}$ 的个位数字 $p \mid a^{p}-a$ 解：待求即为 $7^{222} \bmod 10$ , 上式可写为 $7^{2} \cdot\left(7^{4}\right)^{55} \bmod 10$ 。由于 $(7,10)=1$ , 由 Euler 定理, $7^{2} \cdot\left(7^{4}\right)^{55} \equiv 7^{2} \cdot 1^{55}(\bmod 10)$ , 故 $7^{222} \bmod 10=9$ 即为 $7^{222}$ 之个位数字
$注: 利用Euler 定理,(a = 7, n = 10) = 1, so\ a^{\varphi(n)} = 7^{\varphi(10)} = 7^4 \equiv 1(mod\ 10)\\ 故将7^{222}拆成尽可能多的7^4即可$

归纳与递归¶

数学归纳证明要点¶

证明目标 $P(n)$ 对所有的自然数 $n$ 成立. $/ /$ 需明确定义 $P(n)$ .
证明框架 $/ /$ 例如: 我们对 $n$ 做归纳. 说明将通过归纳来证明.
基础步骤: // 通常比较简单. 写出 $P(0)$
归纳步骤: 写出归纳假设 $P(k)$ , 和待证明的 $P(k+1)$ , 而后证明之。
说明归纳证明完毕. // 必要时重复原命题: 因此, $P(n)$ 对所有的自然数 $n$ 成立. // 或者简单说证毕. 以及 $\square$

思考题：扔煎饼¶

平地上有奇数个人，人之间的距离各不相同。现所有人都朝距其最近的那个人扔煎饼。
试证明：至少有一个人没有挨着煎饼。

$<span class="arithmatex"><span class="MathJax_Preview">Pf.利用归纳法证明\\let\ n = 2k+1, P(n) = 2n+1人参与游戏\\ 1) 基础步骤.P(0):trivial\\ 2)归纳步骤: 假设P(k), \\ P(k+1): 考虑(x,y)表示距离最短的两人，显然他们会互相扔煎饼。\\ 对于剩下2k+1人，若不向这两人扔煎饼，则满足P(k),至少有一人不被扔到；\\ 若有人向这两人扔煎饼，那么由鸽笼原理，这2k+1人必有人没被扔到.\square</span><script type="math/tex">Pf.利用归纳法证明\\let\ n = 2k+1, P(n) = 2n+1人参与游戏\\ 1) 基础步骤.P(0):trivial\\ 2)归纳步骤: 假设P(k), \\ P(k+1): 考虑(x,y)表示距离最短的两人，显然他们会互相扔煎饼。\\ 对于剩下2k+1人，若不向这两人扔煎饼，则满足P(k),至少有一人不被扔到；\\ 若有人向这两人扔煎饼，那么由鸽笼原理，这2k+1人必有人没被扔到.\square$

常见错误¶

平面上任何 $n \geq 2$ 条互不平行的直线必交于一点。证明: 我们对 $n$ 做归纳.

基础步骤: 两条不平行的直线必交于一点
归纳步骤: 假设任何 $k$ 条互不平行的直线交于一点. 对于任意 $k+1$ 条互不平行的直线, 其中: 前 $k$ 条必交于一点, 记为 $p_{1}$ ; 后 $k$ 条必交于一点, 记为 $p_{2}$ ; 考虑到同时属于前 $k$ 条与后 $k$ 条的直线, 必有 $\begin{aligned} & p_{1}=p_{2} \\ \text { 于是这 } k+1 \text { 条互不平行的直线交于一点。 } \end{aligned}$ 原命题归纳证明完毕.
==问题：==错误在于归纳步骤的第一步是错误的。（和后面的情形不同）

强数学归纳法¶

设 $P(n)$ 是与整数 $n$ 有关的陈述, $a$ 和 $b$ 是两个给定的整数, 且 $a \leq b$ . 如果能够证明下列陈述
$P(a), P(a+1), \ldots, P(b)$ .
对任意 $k \geq b, P(a) \wedge \ldots \wedge P(k) \rightarrow P(k+1)$ 则下夗陈述成立
对任意 $n \geq a, P(n)$ .

良序原理¶

良序原理：自然数N的任何非空子集 $S$ 均有最小元素. 所谓“ $S$ 有最小元素” 即 $\exists a \in S(\forall b \in S(a \neq b \rightarrow a<b))

$良序原理与数学归纳法 (归纳公理)的关系【严格说有差异】$

$\Rightarrow$ 【概要】【注：需在皮亚诺公理1-4基础上额外假设每个非 0 自然数都有一个直接前驱】假设 $\forall n \in \mathbf{N} P(n)$ 不成立, 则 $\exists n(\neg P(n))$ 成立. 令 $S=\{n \in \mathbf{N} \mid \neg P(n)\}$ , S非空. 根据良序原理, $S$ 有最小元素, 记为 $m$ , 由奠基步骤, $m \neq 0$ 由 $m$ 的最小性, $(m-1) \notin \mathrm{S}$ , 即 $P(m-1)$ 成立. 根据归纳步骤, $P(m)$ 成立, 即 $m \notin \mathrm{S}$ , 矛盾. 因此, $\forall n \in \mathbf{N} P(n)$ 成立. $\Leftarrow$ 【概要】令 $A$ 为 $\mathbf{N}$ 的无最小元的非空子集, $B=\mathbf{N}-A$ . 基础步骤: $0 \in B$ . 这是因为 $0 \notin A$ , 否则0即其最小元. 归纳步骤: 若 $0, \ldots, n \in B$ , 则 $(n+1) \in B$ . 否则 $n+1$ 是 $A$ 的最小元. 根据归纳原理 $B=\mathbf{N}$ . 这与 $A$ 非空矛盾.

递归¶

基础步骤
递归步骤
排斥规则

结构归纳法¶

广义归纳¶

集合上的良基关系：不存在无限下降的极小元
广义归纳: 对于一个性质 $P$ ,一个集合 $X$ , 及其上的良基关系く, 基础步骤: $P(x)$ 对所有 $X$ 上的极小元 $x$ 成立.
归纳步骤：如果 $P(x)$ 对X上的所有 $y < x'$ 成立，那么 $P(x')成立$ 于是 $P(x)$ 对所有 $x \in X$ 成立.

证明程序的正确性和复杂性¶

Hoare三元组： $\{P\}S\{Q\}$
P成立是权利，Q成立是义务。
部分正确性：不能确保S在有限步内完成
完全正确性

欧几里得算法的正确性¶

只要证明： $\gcd(a_0,b_0) = \gcd(a_k,b_k)\\Pf.\gcd(a,b) = \gcd(b,a\ mod\ b)$

欧几里得算法的复杂度¶

拉梅定理: 设 $a$ 和 $b$ 是满足 $a \geq b$ 的正整数。则欧几里德算法为求出 $\operatorname{gcd}(a, b)$ 而使用除法的次数小于或等于 $b$ 的十进制位数的 5 倍。 $5\left(\left\lfloor\log _{10} b\right\rfloor+1\right)$

计数¶

生成函数¶

简单的说，生成函数是一种把**无限数列**表示成**幂序列的系数**的表示方法。
$F(x) = f_0 + f_1 x + f_2 x^2 + f_3 x^3 + \cdots.$
我们用 $[x^n]F(x)$ 来指代这个生成函数中 $x^n$ 的系数 $f_n.$
例如, 用几何级数的系数来表示数列 $1,1,1, \cdots$ $$ G(x)=1+x+x^{2}+x+\cdots . $$ 又如, $H(x)=1-2 x+3 x^{2}-4 x^{3}+\cdots$ 表示 $1,-2,3,-4, \cdots$ .

离散概率¶

直觉的概率分析¶

四步法¶

选定样本空间 (Find the sample space)¶
样本空间：所有可能结果的集合
定义相关事件 (Define events of interests)¶
确定结果概率 (Determine outcome probabilities¶
计算事件概率 (Compute event probabilities)¶

概率空间: 基于集合论给概率以数学定义¶

定义: 可数**样本空间** $\mathcal{S}$ 乃一个可数集合。
$\delta$ 的每一个元素 $\omega$ 称为一个结果。
定义: 满足下列条件的函数 Pr: $\mathcal{S} \rightarrow \mathbb{R}$ 称为样本空间 $\delta$ 上的一个概率函数:
$\forall_{\omega \in \mathcal{S}} \operatorname{Pr}[\omega] \geq 0$ , 且
$\Sigma_{\omega \in \mathcal{S}} \operatorname{Pr}[\omega]=1$ .
定义: $\mathcal{S}$ 的一个子集 $E \subseteq \mathcal{S}$ 称为一个事件。
事件 $E$ 的概率 $\operatorname{Pr}[E]::=\sum_{\omega \in E} \operatorname{Pr}[\omega]$

基于集合论的概率计算¶

定理 1: 设 $E$ 是样本空间 $\mathcal{S}$ 中的一个事件，事件 $\bar{E}$ （事件 $E$ 的补事件）的概率为:

$\operatorname{Pr}[\bar{E}]=1-\operatorname{Pr}[E]$

定理 2 : 设 $E_{1}$ 和 $E_{2}$ 是样本空间 $\mathcal{S}$ 中的事件, 那么

$\operatorname{Pr}\left[E_{1} \cup E_{2}\right]=\operatorname{Pr}\left[E_{1}\right]+\operatorname{Pr}\left[E_{2}\right]-\operatorname{Pr}\left[E_{1} \cap E_{2}\right]$

条件概率¶

定义: 设 $E$ 和 $F$ 是事件,且 $\operatorname{Pr}[F]>0 . E$ 在给定 $F$ 条件下的概率, 记作 $\operatorname{Pr}[E \mid F]$ , 定义为

$\operatorname{Pr}[E \mid F]::=\frac{\operatorname{Pr}[E \cap F]}{\operatorname{Pr}[F]}$

贝叶斯定理¶

设 $E$ 和 $F$ 是样本空间 $\delta$ 中的事件, $\operatorname{Pr}[E] \neq 0, \operatorname{Pr}[F] \neq 0$ , 则

$\begin{aligned} \operatorname{Pr}[F \mid E] &=\frac{\operatorname{Pr}[E \mid F] \operatorname{Pr}[F]}{\operatorname{Pr}[E]} \\ &=\frac{\operatorname{Pr}[E \mid F] \operatorname{Pr}[F]}{\operatorname{Pr}[E \mid F] \operatorname{Pr}[F]+\operatorname{Pr}[E \mid \bar{F}] \operatorname{Pr}[\bar{F}]} \end{aligned}$

贝叶斯定理的推导¶

由条件概率定义

$\begin{aligned} &\operatorname{Pr}[F \mid E] \operatorname{Pr}[E]=\operatorname{Pr}[F \cap E] \\ &\quad=\operatorname{Pr}[E \cap F]=\operatorname{Pr}[E \mid F] \operatorname{Pr}[F] \end{aligned}$

又

$\begin{aligned} \operatorname{Pr}[E]=& \operatorname{Pr}[(E \cap F) \cup(E \cup \bar{F})] \\ &=\operatorname{Pr}[(E \cap F)]+\operatorname{Pr}[(E \cap \bar{F})] \\ =& \operatorname{Pr}[E \mid F] \operatorname{Pr}[F]+\operatorname{Pr}[E \mid \bar{F}] \operatorname{Pr}[\bar{F}] \end{aligned}$

一些常用说法¶

$\operatorname{Pr}[A]$ 是 $A$ 的**先验**概率。之所以称为 “先验”是因为它不考虑任何 $B$ 方面的因素。
$\operatorname{Pr}[A \mid B]$ 是已知 $B$ 发生后 $A$ 的条件概率或后验概率。
$\operatorname{Pr}[B \mid A]$ 是已知 $A$ 发生后 $B$ 的条件概率或后验概率。
$\operatorname{Pr}[B]$ 是 $B$ 的先验概率, 也作**标准化常量** (normalizing constant)。

事件独立性¶

定义: 事件 $E$ 和 $F$ 是相互独立的当且仅当 $\operatorname{Pr}[E \cap F]=\operatorname{Pr}[E] \cdot \operatorname{Pr}[F]$ 例: 一个有两个孩子的家庭有四种情形 (BB, GG, BG,GB), 假设是等可能的。事件 $E$ 是两个孩子的家庭有两个男孩, 事件 $F$ 是两个孩子的家庭至少有一个男孩。事件 $E$ 和 $F$ 是否独立? 解: $\operatorname{Pr}[E]=\frac{1}{4^{\prime}} \operatorname{Pr}[F]=\frac{3}{4^{\prime}} \operatorname{Pr}[E \cap F]=\frac{1}{4}$

$\operatorname{Pr}[E] \cdot \operatorname{Pr}[F]=\frac{3}{16} \neq \frac{1}{4}=\operatorname{Pr}[E \cap F]$

故 $E$ 和 $F$ 不是相互独立的。

随机变量¶

一个随机变量 $X$ 是一个定义域为某样本空间 $\mathcal{S}$ 的函数。
其伴域(codomain)可为任意非空集合, 但通常取实数集 $\mathbb{R}$ 。即: $X: \mathcal{S} \rightarrow \mathbb{R}$
一个随机变量是一个函数。它既不是一个变量, 也不是随机的。

条件期望¶

给定一个随机变量 $R, R$ 在已知事件 $A$ 条件下的期望值是 $R$ 在 $A$ 中结果上的取值的概率加权平均值:

$\operatorname{Ex}[R \mid A]=\sum_{r \in \operatorname{range}(R)} r \cdot \operatorname{Pr}[R=r \mid A]$

例: 已知一个公平骱子投出的点数不小于 4 点, 此条件下投出的点数的期望值是多少?

$\operatorname{Ex}[R \mid R \geq 4]=\sum_{i=1}^{6} i \cdot \operatorname{Pr}[R=i \mid R \geq 4]$

闭包¶

闭包的定义¶

设 $R$ 是集合 $\mathrm{A}$ 上的关系， $\mathrm{P}$ 是给定的某种性质（如：自反、对称、传递），满足下列所有条件的关系 $R_{1}$ 称为 $R$ 的==关于 $\mathrm{P}$ == 的闭包:
$R \subseteq R_{1}$
$R_{1}$ 满足性质 $\mathrm{P}$
如果存在集合 $A$ 上的关系 $R^{\prime}, R^{\prime}$ 满足性质 $\mathrm{P}$ 并包含 $R$ , 则 $R_{1} \subseteq R^{\prime}$ ,
自反闭包 $r(R)$ 、对称闭包 $s(R)$ 、传递闭包 $t(R)$

闭包的计算公式¶

传递闭包的Warshall算法¶

传递闭包： $t(R) = R\cup R^2 \cup R^3 \cdots \cup R^n$

$\therefore M_{t(R)} = M_R \or M_R^2 \or M_R^3 \or M^n_R$

复杂度： $O(N^4)$

$反思：如果在之前的情况下\\ 已经得到了a -b有长度为n-1的路径，\\那么没有必要现再寻找是否存在长度为n的路径$

Warshall: $$ W_k[i,j] = 1\ iff. W_{k-1}[i,j] = 1\ or ( W_{k-1}[i, k] = 1)\and( W_{k-1}[k, j] = 1)\ 复杂度：O(N^3) $$

等价关系¶

满足性质：自反、对称、传递。
“等于”关系的推广
例子

对3同余关系

$R \subseteq N \times N, x R y$ iff 存在正整数 $k, l$ , 使得 $x^{\mathrm{k}}=y^{\mathrm{l}}$ 。

自反: 若 $x$ 是任意自然数, 当然 $x^{k}=x^{k}$ ;
对称: 若有 $k, l$ , 使 $x^{k}=y^{l}$ ; 也就有 $l, k$ , 使 $y^{l}=x^{k}$ ;
传递: 若有 $k, l$ , 使 $x^{\mathrm{k}=y^{1}}$ ; 并有 $m, \mathrm{n}$ , 使 $y^{\mathrm{n}}=z^{\mathrm{m}}$ ; 则有 $x^\mathrm{kn}=z^{\mathrm{ml}}$

等价类¶

- $R$ 是非空集合 $\mathrm{A}$ 上的等价关系, $\forall x \in \mathrm{A}$ , 等价类 ${[x]_{R}}=\{y \mid y \in \mathrm{A} \wedge x R y\}$ （等价类是一个集合）¶

每个等价类是A的一个非空子集。
例子: 对 3 同余关系: $R \subseteq Z \times Z, x R y$ 当且仅当 $\frac{|x-y|}{3}$ 是整数。
3 个等价类

$\begin{aligned} &[0]=\{\ldots,-6,-3,0,3,6,9, \ldots\};\\ &{[1]=\{\ldots,-5,-2,1,4,7, \ldots\} ;} \\ &{[2]=\{\ldots,-4,-1,2,5,8,11, \ldots\}} \end{aligned}$

商集¶

$R$ 是非空集合 $A$ 上的等价关系, $\forall x \in A$ , 则其所有等价类的集合称为商集, $A / R$
集合 $A=\left\{a_{1}, a_{2}, \ldots, a_{\mathrm{n}}\right\}$ 上的恒等关系 $I_{\mathrm{A}}$ 是等价关系, 商集 $A / I_{\mathrm{A}}=\left\{\left\{a_{1}\right\},\left\{a_{2}\right\}, \ldots,\left\{a_{\mathrm{n}}\right\}\right\}$
定义自然数集的笛卡儿乘积上的关系 $R$ : $(a, b) R(c, d)$ 当且仅当 $a+d=b+c$ 证明这是等价关系, 并给出其商集.

集合的划分¶

把一个集合分为若干**不相交**的块，并保证这些块加和为全集

偏序关系（partail order）¶

自反、反对称、传递

全序（线性序）¶

定义：R为非空集合A上的偏序关系

$\forall x,y \in A, x与y都是可比的，则称R为全序$

实例：数集上的小于或等于关系是全序关系

整除关系不是正整数集合上的全序关系

覆盖¶

定义： $x,y \in A,如果x < y且不存在z使得z \in A 使得 x < z < y,则称y覆盖x.$

偏序集（p.o.set）与哈斯图¶

偏序集¶

哈斯图（Hasse Diagrams）¶

偏序关系简化

省略所有顶点上的环（(a,a),(b,b),(c,c)）
省略所有因传递关系而引出的边（去除**非覆盖边**）((a,c)) $i.e.确保每条边都是覆盖关系$
根据箭头方向自下而上重排列所有顶点，而后将所有的有向边替换为无向边