支配集\覆盖集\独立集\支配与着色¶

知识点¶

支配集\点覆盖集\点独立集¶

支配集(这些点支配其他所有点)¶

无向图 $G = <V,E>$ ,取 $V^* \sube V$ ,使得对于 $\forall v_i \in V-V^*$ ,都能在 $V^*$ 中找到一个点与其相连.就称 $V^*$ 为支配集.

极小支配集
最小支配集
G的支配数为最小支配集中顶点的个数.记作 $\gamma_0(G)$ .

(点)独立集¶

无向图 $G = <V,E>$ ,取 $V^* \sube V$ ,使得 $V^*$ 中任意两个点都不相邻,则称为G的(点)独立集

极大独立集
最大独立集
G的点独立数为最大独立集中的顶点数.记作 $\beta_0(G)$

定理¶

极大独立集**都是**极小支配集,反之不然

点覆盖集(点覆盖所有边)¶

无向图 $G = <V,E>$ ,取 $V^* \sube V$ ,使得G中任意一条边,都有 $V^*$ 中一个顶点相关联.则成为G的点覆盖集.简称为点覆盖.

极小点覆盖
最小点覆盖
点覆盖数为最小点覆盖中的顶点数,记作 $\alpha_0(G)$ .

定理¶

$V^*$ 为G的点覆盖 $\iff$ $\overline{V^*} = V-V^*$ 为G的点独立集.
推论: $V^*$ 为G的极小(最小)覆盖 $\iff$ $\overline{V^*} =V-V^*$ 是G的极大(最大)点独立集,从而有 $\alpha_0 +\beta_0 = n$ .

边覆盖集与匹配¶

边覆盖(边覆盖所有点)¶

设G没有**孤立点**, $E^* \sube E$ (注意这是一个**边集**),使得 $\forall v \in V$ , $\exist e \in E^*$ , $e与v关联$ .则称 $E^*$ 为G的边覆盖(集)

极小边覆盖
最小边覆盖
边覆盖数为最小边覆盖中的边数,记作 $\alpha_1$ .

匹配(边独立集)¶

一个边集,其中所有元素都不相邻.

极大匹配(极大边独立集)
最大匹配(最大边独立集)
匹配数(边独立数)为最大匹配中的边数,记作 $\beta_1$ .

设M为图 $G = <V,E>$ 的一个匹配,

称M中的边为匹配边,不在其中的边为非匹配边
与匹配边相关联的点成为**饱和点**(不能再连其他边,因此饱和),不与匹配边关联的点为非饱和点.
若G中每一个定点都是饱和点,则称M为G的**完美匹配**.(每一个点都有边关联,都被匹配到)
G中由**匹配边**与**非匹配边**交替构成的路径叫做**交错路径**,起点和终点都是**非饱和点**的交错路径成为**可增广的交错路径**,交替构成的圈称为**交错圈**(显然是偶圈).

注:为什么边独立集叫做匹配?

笔者的理解是,匹配要求一个点不能被匹配超过一次,也就是边与边不能相邻(类比一男不能脚踏两条船),因此我们从图中选取一些**不相邻**的边,在就构成了符合条件的匹配.

定理¶

设n阶图G中无孤立点.

(1)设M为G的一个最大匹配,对G中每一个 $M-$ 非饱和点均取一条与其关联的边,组成边集N,则 $W = M\cup N$ 为G的最小边覆盖.

(2)最小边覆盖中移去相邻的边中的一条得到的匹配为最大匹配

(3)边覆盖数 $\alpha_1+$ 匹配数 $\beta_1= n$ .

各种集合的总结¶

覆盖-独立-支配
$\alpha_0 + \beta_0 = n$ .
$\alpha_1 + \beta_1 = n$ .
$\gamma_0$ 自称一派.

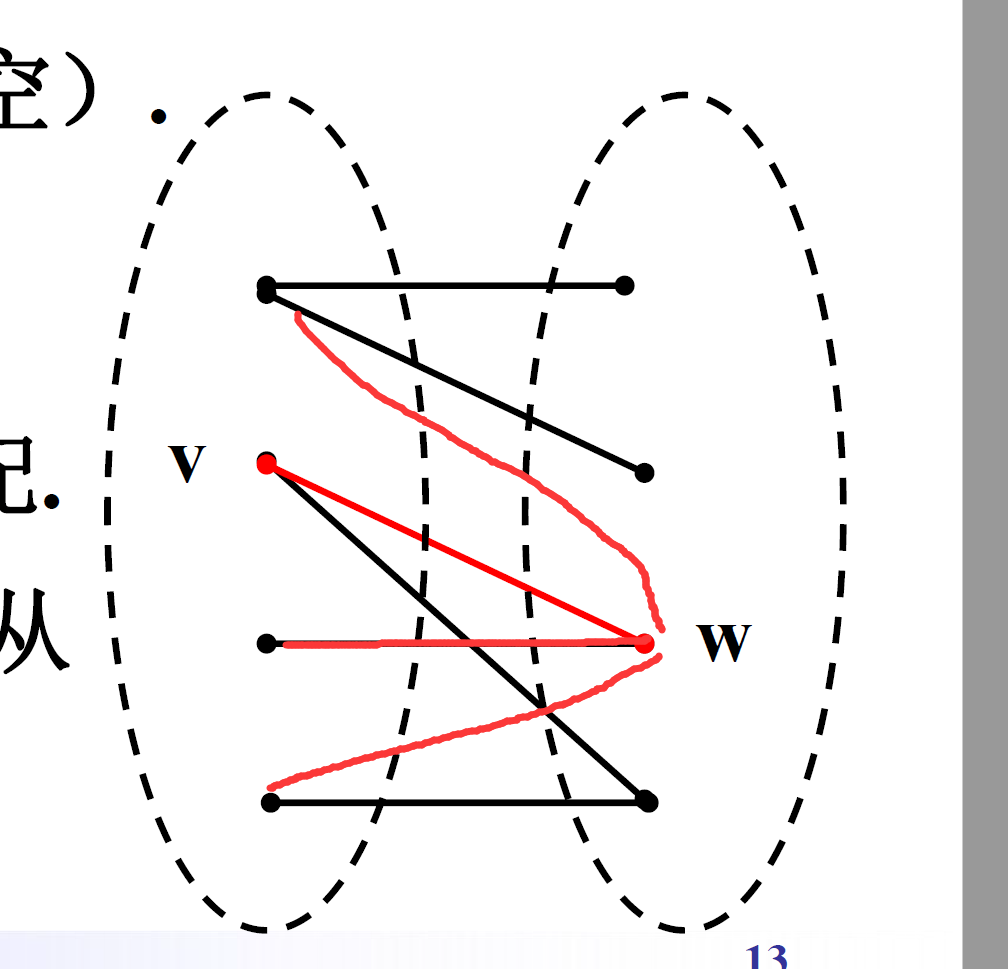
Berge定理¶

设M是G的一个匹配,则M是G的最大匹配 $\iff$ G中不含有关于M的可增广路径.

二部图的匹配¶

设 $G = <V_1,V_2,E> <span class="arithmatex"><span class="MathJax_Preview">为二部图,</span><script type="math/tex">为二部图,$ |V_1| \le |V_2||V_1| \le |V_2|,M为G的一个匹配.当 $|M| = |V_1|$ ,称M为 $V_1$ 到 $V_2$ 的**完备匹配**.

完备匹配一定是最大匹配,因为所有 $V_1$ 中的点都被饱和了,但不一定是完美匹配.

当且仅当 $|V_1| = |V_2| =|M|$ 时,M是**完美匹配**.

完备匹配的充要条件-Hall定理¶

G中存在 $V_1$ 到 $V_2$ 的完备匹配 $\iff V_1$ 中任意 $k(k = 1, 2, \cdots, |V_1|)$ 个顶点**至少**与 $V_2$ 中 $k$ 个顶点相邻.

即, $\forall i = 1,2,3,\dots, |V_i| \le |N(V_i)|.$

归纳证明.

(1)对 $V_{1}$ 的任意真子集 $A,|N(A)|>|A|$ 任取一个顶点 $\mathbf{v} \in \mathbf{V}_{1}$ , 任取 $\mathbf{w} \in \mathbf{N}(\{\mathbf{v}\})$ . $\mathbf{H}=\mathbf{G}-\{\mathbf{v}, \mathbf{w}\}$ 是一个二部图（非空） H满足归纳假设的条件, 从而 $H$ 有 $V_{1}-\{\mathbf{v}\}$ 到 $V_{2}-\{\mathbf{w}\}$ 的完备匹配. 这个匹配加上边 $(v, w)$ 构成 $G$ 的从 $V_{1}$ 到 $V_{2}$ 的完备匹配.

说明

为什么要分成 $|N(A)| > |A|$ 的情况?

因为这样的话,就有 $|N(A| \ge |A|+1)$ ,我们删去点v,w后,即使对于w的最坏的情况,即w连了尽可能多的边,那么删去w后,对于 $V_1 = V-v$ ,每个点的度数保持不变或者减1,因此对于 $V_1$ ,我们仍有 $\forall V_i \sub V_1, |V_i| \le |N(V_i)|$ .

完备匹配的充分条件-t条件¶

若 $V_1$ 中每个顶点至少关联 $t$ 条边,且 $V_2$ 中每个顶点至多关联 $t$ 条边.则存在完备匹配.

习题¶

完备匹配\完美匹配¶

$\text { 一个无回路的简单连通图最多只有一个完美匹配。(完美匹配指能饱和所有顶点的匹配) }$

即证一棵树至多有一个完美匹配.

构造法证明

对每个叶子结点，它只能和唯一与它相邻的那个点匹配如果一个结点连了两个或以上的叶子结点，那么这两个叶子结点中至少有一个是不能匹配的所以，只有当每个结点最多只和一个叶子结点相邻的时候，才会存在完美匹配去掉叶子结点以及与其相邻的点，会得到若干不连通的树重复上面的过程，直到所有的结点都被匹配或者有点不能被匹配由于在任意阶段，每个结点最多只会和一个叶子结点相连，所以这个匹配的方法都是被唯一确定下来的因此一棵树最多只有一种完美匹配的方法。

令 $k$ 为一整数。对于任意有限集合, 证明对它的任意两个 $k$ 划分都存在一个相同的代表集。
集合的 $k$ 划分指划分为大小相同的互不相交的 $k$ 个子集, 为简便起见, 设集合的大小为 $k$ 的整数倍从而每个子集均有相同个元素。
一个划分的代表集指从每个子集中取出一个元素而构成的集合。举例：集合 $\{1,2,3,4\}$ 的一个 2 划分为 $A:\{1,2\}\{3,4\}$ 。此划分的代表集有 $\{1,3\},\{2,3\},\{1,4\},\{2,4\}$ , 但 $\{1,2\}$ 不是其代表集。集合的另外一个划分为 $B:\{2,3\}\{1,4\}$ 。易见, $A$ 与 $B$ 存在相同的代表集 $\{1,3\}$ 。

解析

难点在于怎么将题目转化为图的问题.

两个划分各自构成二部图的两边，划分中的子集相邻当且仅当这两个子集有相同元素.

于是由t-条件,存在一个完备匹配,且是完美的.

注意到题目条件**对所有 $k \le$ n,任意k个集合的并集至少包含 $k$ 个元素**,这句话非常像二部图完备匹配的充要条件(Hall定理)

稍微难的地方在于建图:什么作为点?什么作为关系?

二部图匹配应用¶

经典染色问题.

对方格间隔染色.不难发现任意的小矩形都有1黑1白,而相同颜色的方格不能出现在同一个小矩形上.这构成一个二部图.而要求裁成若干小矩形,就要求存在完美匹配.

而显然 $|V_1| \ne |V_2|$ .故不存在完美匹配.

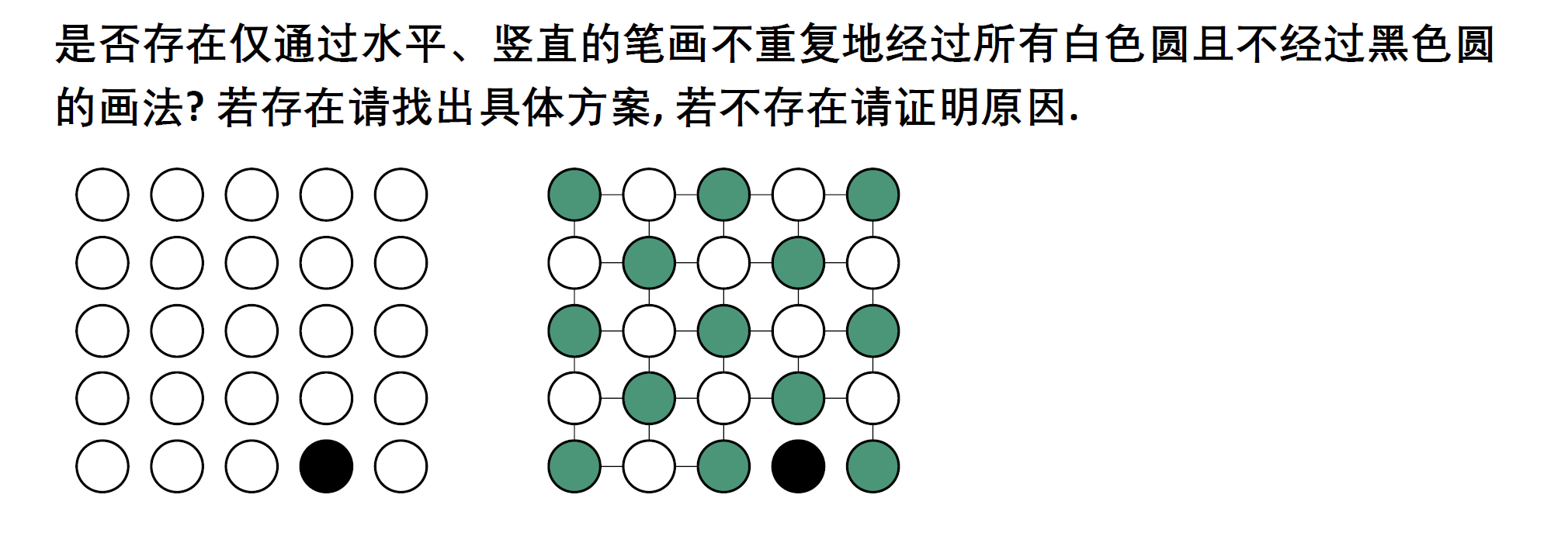
交错路径¶

对圆圈间隔染色,不难发现任意一条边必须经过一个绿色和一个黑色,因此最终得到的路径必然是绿白交错的,根据小学的植树原理,绿色的圆圈要么与白色相等,要么与白色相差1,而这里有13个绿圈,11个白圈,显然不能构成一条简单路径.