树¶

知识点¶

树的前序\中序\后序遍历¶

$树\to 序列$

前序:根-左-右
中序:左-根-右
后序:根-左-右
层序:逐层
思考:
仅知道前序\中序\后序中的一种序,能够还原树吗?
如果知道其中的两个,能够还原树吗?

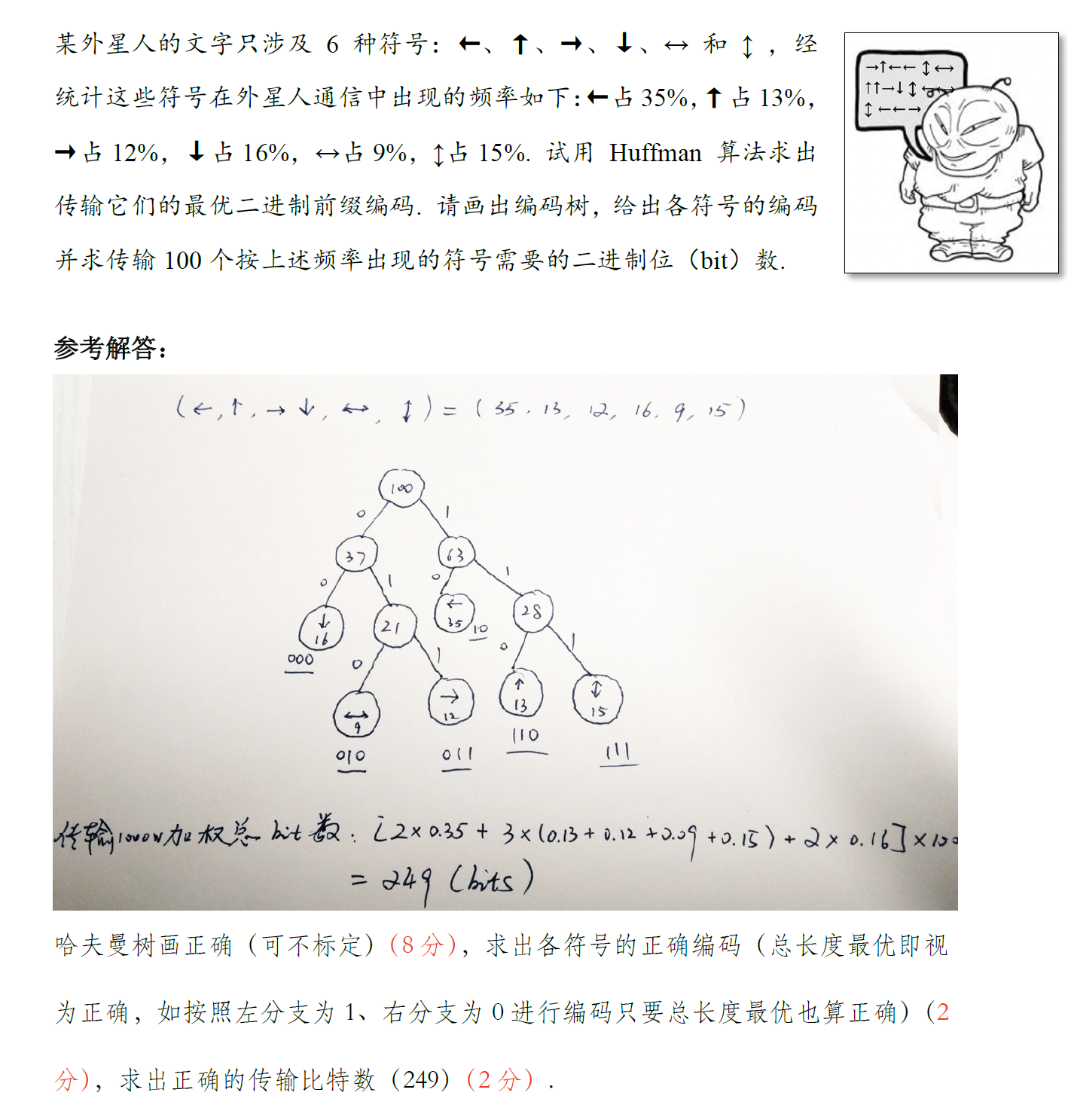
霍夫曼编码¶

countEveryDigit();
makeTree();
for(int i = 0; i < n-1; i++) {
    sort();
    pickLeastTwo();
    combine();
    add();
}
addCode0_1();
return;

习题¶

树的性质¶

记 $P_i$ 为度数为 $i$ 的节点数.证明: $\sum_{i = 1}^{n-3} i P_{i+2} = 2.$
$\text { 证明或反驳：若 } G \text { 是最大度大于等于 } k \text { 的树, 则 } G \text { 至少有 } k \text { 个顶点度数为 } 1 \text { 。 }$
$\text { 证明或反驳：所有边数不超过图 } G \text { 的最小顶点度的树都与图 } G \text { 的某个子图同构 (只考虑简单图)。 }$

笔者思路

令 $D=\left(d_{1}, d_{2}, \cdots, d_{n}\right)$ 为一正整数序列, 且 $n \geq 2$ 。 a) 若 $D$ 恰好是某个树 $T$ 的各个顶点的度数序列, 试证明 $$ \sum_{i=1}^{n} d_{i}=2(n-1) $$ b) 反过来, 试证明：若 $D$ 满足上式, 则存在一个树 $T$ , 使得 $D$ 恰好是 $T$ 的各个顶点的度数序列。

笔者思路

(b)问可以采用构造证明,即,证明对于任意的合法度序列,都可以构造出至少一种树.

算法:

对于所有度数大于1的顶点,先选最大的那个作为根, 这将产生 $\Delta G$ 个叶子节点,然后从大到小依次向当前的树中的叶子节点上添加新点,增加$\delta_i -2 $个叶子节点.

记内点有 $M$ 个,叶子有 $L$ 个, $M+L = n.$

刚才构造产生的叶子节点共 $\sum_{i=1}^M(\delta_i - 2) + 2 = 2n-2 - (n-M) -2M +2 = n-M = L$ 个.正好对应剩余的L个1度顶点.

构造过程以及构造结束后,都可以保证当前的图是一棵树.

构造所有非同构的n阶树¶

利用 $\sum \delta_i = 2m = 2(n-1)$ 构造所有度序列

每一种度序列可能对应多种不同构的树,不同度序列的树一定是非同构的.

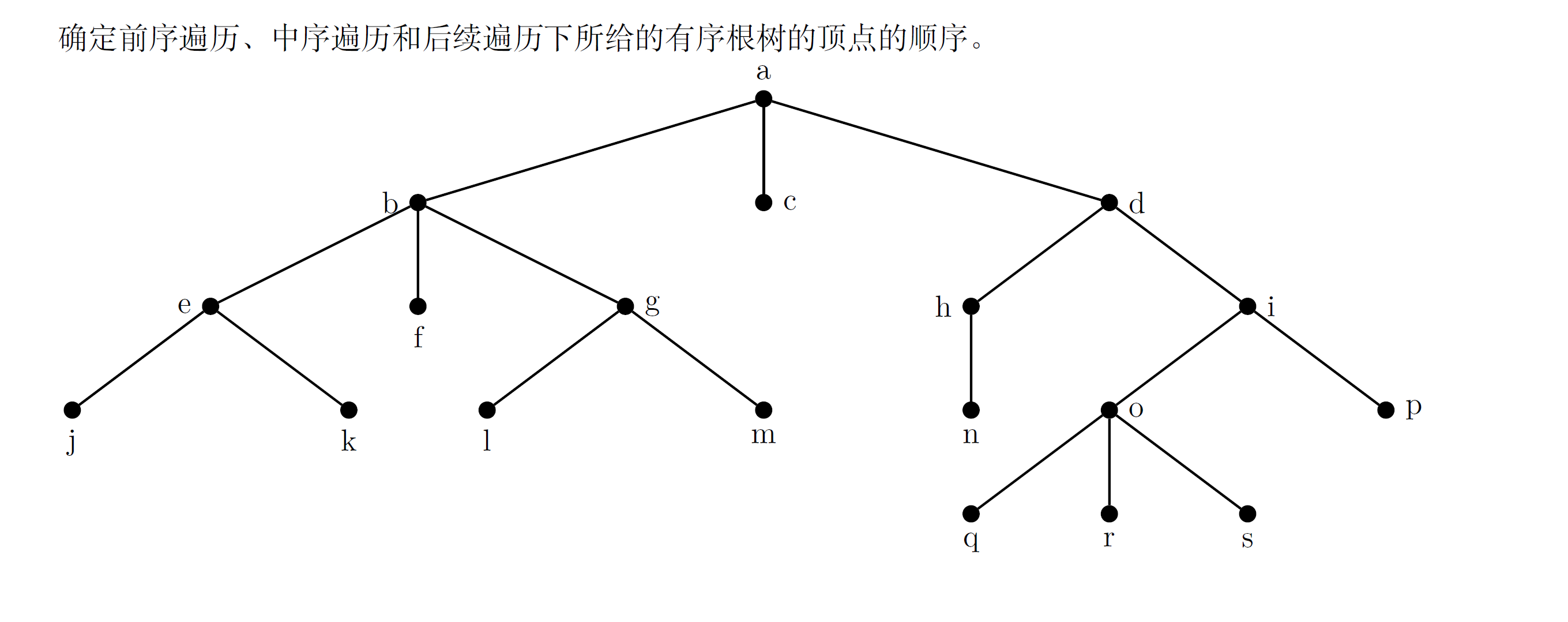
preorder/inorder/postorder traverse¶

preorder: $a(b(e(j\ k)\ g(l\ m)))(d(h(n)\ i(o(q\ r\ s)\ p))$

inorder: NULL

postorder: $(((j\ k)e)f((l\ m)g)b)(((n)h)(((q\ r\ s)o)(p)i)d)a$

决策树¶

若一枚伪币与其他硬币质量不等, 那么为了在 7 枚硬币中找出这枚伪币, 用天平称量找出伪币的方案在最坏情况下最少要多少次? 并给出相应方案（画出决策树）。

笔者思路

对可能的称法进行尝试

$3 - 3 + 1$

相等,则假币就是剩下的一枚,1次

不等,则假币在这两堆中

$1-1+1$ (对两堆都做)

相等

随机拿一枚与剩下的那一枚称,若相等,则说明没有假币,

若不等,则说明剩下就是假币

不等

随机取一枚与剩下的称,若相等,则另一枚就是

若不等,则两次都称的那一枚就是

在这种方案下,最坏需要5次

$2-2+3$

相等,假币一定在3里,由刚才分析,需要两次才能从中找出假币,那么一共3次

不等,则假币在4里,

从两堆中随机各取一枚,

若相等,则假币在剩下2枚里,还要再比一次,一共3次

若不等,则假币就在这2枚里,还要再比一次,一共3次

在这种方案下,最坏需要3次

可以证明,没有比3次更少的方案了,故答案为3次.

反思

注意到对于给定 $k$ 枚硬币,以及是否确定里面有假币两个参量,就可以确定对应的最小次数.

因此可以写出动态规划算法.

树的应用¶

时刻牢记树的定义:无环连通图. 一旦发现了这个性质,立即可以利用数的结论.

霍夫曼编码¶

只要记得算法就行