代数系统-群与环¶

处理小阶群的技巧, 15阶以下群的分类 - 知乎 (zhihu.com)

如何直观地理解群论？ - 知乎 (zhihu.com)

知识点¶

群的定义¶

半群\独异点\群都是**一个**二元运算的**代数系统**.

**可结合**的 $\to$ 半群[semi-group]
$可结合\and有单位元\to$ 幺半群(独异点) [monoid] $V=<S, \circ, e>$
$独异点\and 任意元素有逆元\to$ 群 $G= <S, \circ, e, -1>$

**结合律**是群的出发点,几个要素:

(封闭性)

结合律

单位元

逆元

典型的群¶

整数加群有理数加群实数加群复数加群
模n剩余加群

八阶以下群的结构:

总结:

一阶群(1)
二阶群(1)
三阶群(1)
四阶群(2)
Klein四元群
- 可交换
- 每个元素逆元就是自己
- $a,b,c$ 中任意两个元素运算结果为另一个.
四阶循环群
五阶群(1)
六阶群(2)
二面体群 $D_3$
六阶循环群
七阶群(1)
八阶群(5)

元素的幂 k阶元¶

定义群中元素的幂 $$ a^n = \begin{cases} e,& n = 0\ a^{n-1}a,& n > 0\ (a^{-1})m,& n <0, m = -n. \end{cases} $$

这个定义可以推广到半群(n为正数),独异点(n为自然数).

定义使得等式 $a^k = e$ 成立的**最小正整数k**成为a的阶,记作 $|a| = k$ ,若不存在这样的k,则成a为无限阶元.

幂的运算性质¶

$(ab)^{-1} = b^{-1}a^{-1}$
$(a^m)^n = a^{mn}$
若G为交换群,则 $(ab)^n = a^nb^n$

不要想当然,群**默认是不满足交换律的**!!

群的性质¶

消去律¶

群结构，八阶及以下的群 - 简书 (jianshu.com)

元素的性质¶

设G为群, $a\in G$ ,且 $|a| = r$ .

$a^k = e \iff r|k$

注意:这个公式非常重要!

简单来说,如果能够证明 $a^k= e$ 那么这个数一定是a的阶的整数倍.涉及元素阶的问题经常使用这个定理.

$|a^{-1}| = |a|$

子群¶

判定定理¶

验证对乘法\逆元封闭
$\forall a,b \in H \to ab^{-1} \in H$ (可以视为1的等价表示)
(有穷集) $\forall a,b\in H \to ab\in H$ .(说明对于有穷集合,只需验证对乘法封闭)

$Pf. let\ S = \{a,a^2, \dots \}(a \ne e),\\ \because |S|\ is \ finite, \therefore \exist i < j, a^i = a^j \Rightarrow a^{j-i} = e(j-i > 1)\\ \Rightarrow a\cdot a^{j-i-1} = e \Rightarrow a^{-1 } = a^{j-i-1}.$

这就验证了逆运算的封闭性.

由元素a生成的子群¶

$H = \{a^k| k\in \Z\} = <a>.$

由B生成的子群¶

B是G的一个子集,记所有包含B的子群的交(可以证明也是子群),记作 $<B>= \cap\{H|B\sube H \and H \le G\}$ .

这个子群的所有元素都是B中元素或其逆元.

注意到,这里子群使用了" $\le$ "符号,因为其满足偏序关系,由此我们可以定义**子群格**

子群格¶

$S = {所有G的子群},\forall A,B \in S, ARB \iff A \le B$

思考:为什么子群能够构成格?

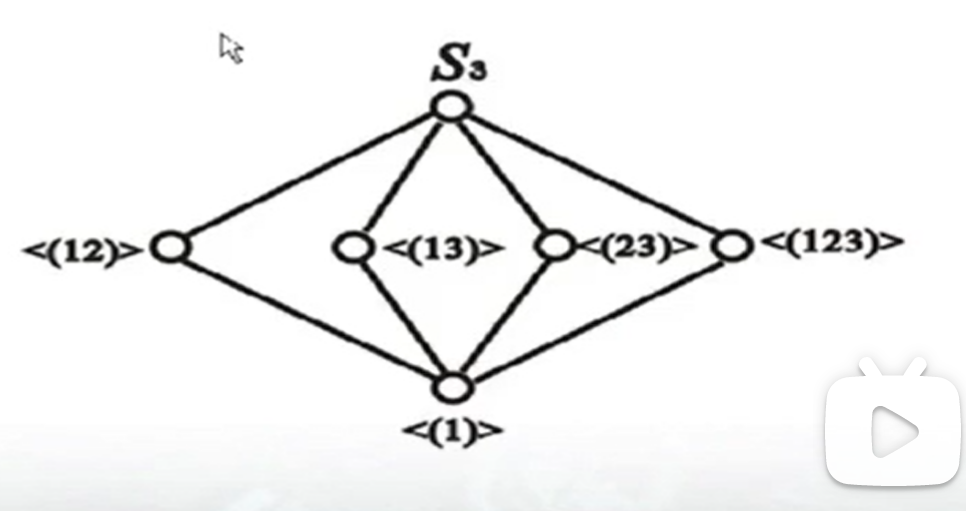
例子: 3元对称群的子群格(Subgroup Lattice)

群的分解¶

陪集¶

设H是G的子群, $a\in G$ ,令 $$ Ha = {ha| h \in H} $$ 称Ha是子群H在G中的右陪集,称a为Ha的代表元素.

右陪集的性质¶

$H \le G,\forall a,b \in G,\\ a\in Hb \iff ab^{-1} \in H \iff Ha = Hb.$

证明不难,抓住群的逆元和结合律即可.

但是要看到宏观的含义:

$a\in Hb \iff Ha = Hb$ 这有益于**陪集的划分**.

$a\in Hb \iff ab^{-1} \in H \iff Ha = Hb$ 给出了两个右陪集相等的充要条件.并且说明**右陪集中任一元素都可以作为其代表元素!!**

右陪集的划分¶

$定义G上二元关系,\forall a,b \in G,\\ <a,b> \in R \iff ab^{-1}\in H \iff a \in Hb \iff Ha = Hb.$

这个关系具有自反\对称\传递性.是等价关系.因此可以据此对所有右陪集进行**划分**.

$[a]_R = Ha$

推论 $$ (1) Ha = Hb \or Ha \cap Hb = \empty\ (2) \cup{Ha| a \in G} = G $$

推论2很重要,这说明陪集和群的关系.

正规子群(不变子群)¶

$Ha = aH$ .即一个群的左右陪集相等.

注：

(1) 任何群G都有正规子群，因为G的两个平凡子群G和{e}都是G的正规子群。(对于任意群G, $aG = Ga =G$ )

(2) 若G是交换群，则G的所有子群都是正规子群。(显然)

左右陪集的关系¶

H在G中的左右陪集的个数是相同的.

因此统称左陪集数和右陪集数为H在G中的陪集数,也称作H在G中的**指数**,记作 $[G:H]$ .

Lagrange定理¶

G为有限群,H是G的子群,则**群G的阶数**等于**子群H的阶数**与**H关于G的指数**之积, 即 $$ |G| = |H|\cdot [G:H] $$

$Pf.\\ |G| = \sum |Ha_i|, i = 1,2,\dots, r\\ \because |Ha_i| = |H|(可用反证法证明)\\ \therefore \sum |Ha_i| = [G:H]\cdot |H|.\square$

注意到H是G的任意子群,这就说明任意子群的阶数都是G的阶数的因子.

推论

$设G是n阶群,则\forall a \in G, |a|是n的因子,且a^n = e.\\ Pf. 由Lagrange\ Thm. 因为<a>是G的子群,因此|<a>|是n的因子,后半部分显然.$
若G是**素数阶**群,则存在 $a\in G \to <a> = G$ .

这个结论往往用来等价表示一个群(循环群).

Cauchy定理¶

群论Cauchy定理的另一种证法，以及引申 - 知乎 (zhihu.com) $$ \text { Cauchy定理：若群 } G \text { 的元素个数能被素数 } p \text { 整除，则其必有以 } p \text { 为阶的元素。 } $$

循环群¶

定义¶

若存在 $a\in G, <a> = G$ , 则称G为循环群.a为G的生成元.

根据a的阶数,可以分为:

n阶循环群
无限循环群

求所有生成元¶

无限循环群 $<a>$ 的生成元只有 $a, a^{-1}.$
n阶循环群有 $\phi(n)$ 个生成元,对于任何小于n且与n互素的自然数 $r$ , $a^r$ 是G的生成元.

求循环群的所有子群¶

$G = <a>$ 是循环群,则G的子群仍是循环群.
G是n阶循环群,则对于n的每一个正因子d,G**恰好有一个**d阶子群.

对于n阶循环群,先求出n的所有因子d,对于每一个正因子d, $<a^{n\over d}>$ 是G唯一的d阶子群(任意阶循环群只有一个).

注意:循环群的所有子群都可以由群的元素生成. 非循环群不是如此, 例如, 没有任何一个元素能够生成这个群自身.

置换群¶

群论(3): 置换群 - 知乎 (zhihu.com)

离散数学（全）-北京大学_哔哩哔哩_bilibili P 57

置换作为运算¶

设 $S= \{1,2,\cdots, n\}$ ,S上的任何**双射**函数: $S^S$ 成为S上的n元置换.

强调置换的一个重要性质: 双射

对于 $\forall \sigma \in S_{n}$ , 我们记 $\sigma=\left[\begin{array}{cccc}1 & 2 & \cdots & n \\ \sigma(1) & \sigma(2) & \cdots & \sigma(n)\end{array}\right]$ .

置换的乘积:置换的置换仍是置换,类似于函数的复合.(满足封闭性)
$k$ -轮换,特别的 $k=2$ 时,成为对换
置换的分解:
置换可以分解为**不交的**轮换之积,且"表示法唯一"(忽略交换这些轮换的顺序)

因此,我们可以分析一个置换的结构:

$\sigma = 1^{C_1(\sigma)}2^{C_2(\sigma)}\cdots n^{C_n(\sigma)}$ ,其中 $C_n(\sigma)$ 表示n轮换的个数

$\sum i\cdot C_i(\sigma) = n.$
进一步的,任何置换可以表示成**奇偶性相同的**若干对换之积(奇偶性相同是指对换的数目的奇偶性相同),(注意这样的分解结果是不唯一的,如果你乐意,你甚至可以一直对换下去)

按照这个标准,所有的置换可以分为**奇置换**与**偶置换**.
置换的乘法：函数的合成例如: 8 元置换 $\sigma=(132)(56-18), \tau=(18246573)$ , 则 $$ \sigma \tau=(15728)(3)(4)(\sigma)=(15728) $$ 置换求逆：求反函数 $$ \sigma=(132)(5648), \quad \sigma^{-1}=(8465)(231) \text {, } $$

Trick:在理解轮换运算时,可以画成轮图:

这些过程可以联系线性代数的行变换

置换作为群¶

由上,不难发现置换运算满足群的定义.因此,

令 $S_{n}$ 为 $\{1,2, \ldots, n\}$ 上所在n元置换的集合.

$S_{n}$ 关于置换乘法构成群, 称为 $\bold{n}$ 元对称群. $|S_n| = n!$
$S_{n}$ 的**子群**称为 $\bold{n}$ 元置换群.
$S_n$ 的所有偶置换的集合构成**n元交错群**. $A_n \le S_n,A_n = {n!\over 2}$
对于 $S_n$ 来说,它的所有子群都称作n元置换群,n元对称群 $S_n$ \n元交错群 $A_n$ 都是n元置换群的特例(虽然感觉这么说怪怪的)

例 3 元对称群 $S_{3}=\{(1),(12),(13),(23),(123),(132)\}$ 3元交代群 $A_{3}=\{(1),(123),(132)\}$

元素的阶¶

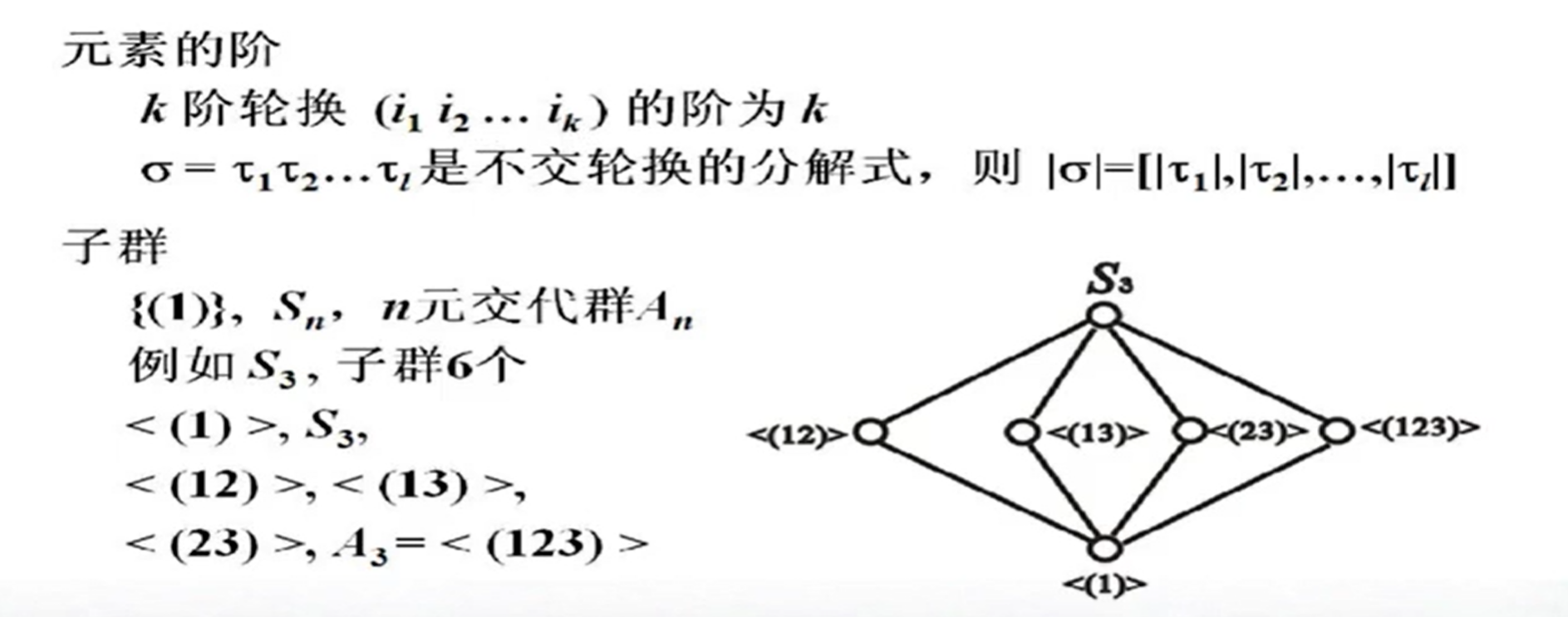
说明

元素的阶定义: 最小正整数 $k, s.t.\ a^k = e$ ,对于k阶轮换,容易发现至少需要重复k次才能回到原点.因此 $\tau^k = e = (1).$

因此对于任意一个置换,我们总可以分解为若干轮换之积,那么该元素的阶就是所有轮换的**最小公倍数**.

Cayley 定理¶

环与域¶

习题¶

群的性质¶

总结:

证明群中元素相等的办法就是用结合律\消去律\单位元及逆元的性质\群的幂运算规则等对等式进行**变形和化简**.

证明子集相等的基本方法就是证明两个集合相互包含

证明两个元素的阶相等\整除的基本方法是利用*元素的阶的那个定理*

可能用到1阶或2阶元的充分必要条件是 $a^{-1} = a$ .

设 $G = \{a_i|i = 1, 2, \cdots ,n\}, a_iG = \{a_ia_j|j = = 1, 2, \cdots ,n, \}$ 证明 $a_iG = G$

即证(1) $a_iG \sub G$ (2) $a_iG <span class="arithmatex"><span class="MathJax_Preview">不是</span><script type="math/tex">不是$ GG的真子集

(1)显然

(2)反证,若是,则有 $|a_iG| < |G| \Rightarrow j \ne k, a_ia_i = a_ia_k \Rightarrow a_k = a_j,与|G| = n$ 矛盾.

$\because a_iG = G$ ,而 $a_iG$ 在G的运算表中就是第i行的所有运算结果,这就说明**G的运算表中每一行(列)都是G的元素的一个排列**,注意这是一个必要条件,也就是说,如果一个运算表不满足这个性质,那么一定不是群,反之不然.

证明偶阶群必含2阶元

[笔者解法]

反证法

若不含2阶元,则不含任意偶数阶元,即所有元素的阶数都是奇数.

因此整个群的结构可以表示为 $\{e, i_1,i_1^2, \cdots ,i_1^{2k_1}, i_2, i_2^2,\cdots i_2^{2k_2}, \cdots \}$ ,因此这个群的阶数为奇数,与前提矛盾.

[课本解法]

注意到$x^2= e \iff |x| = 1 \or |x| =2 $

又因为 $|x| = |x^{-1}|,$ 而对于阶数大于2的元素,有 $x \ne x^{-1}.$

因此所有大于等于3阶的元素都是与其逆**成双成对**出现的,这部分的元素个数为偶数.

又因为不含二阶元,那就只剩下单位元,

那么群的阶数就是奇数,与前提矛盾.

证明元素的阶相同求元素的阶¶

这类题目的证明往往用到 $if\ |a| = r, a^n = e \to r |n .$

如果要证明 $r_1 = r_2$ ,往往证明 $$ a_2^{r_1} = e \Rightarrow r_2 |r_1\ a_1^{r_2} = e \Rightarrow r_1|r_2 \ \Rightarrow r_1 = r_2. $$

若元素 $x, g \in G$ ，证明: $\operatorname{order}(x)=\operatorname{order}\left(g x g^{-1}\right)$ 。对于任意两个元素 $x, y \in G$ ，证明: order $(x y)=\operatorname{order}(y x)$
$设G为群,x,y \in G, yxy^{-1} = x^2, 其中x不是单位元,y是二阶元,求x的阶.$

此题难度在于充分利用群的性质将公式合理变形(但是只要你相信可以化出来,就一定可以化出来) $$ \begin{align} (1)& yx^2y = x^4\ (2)& x^2y = yx\ &\because |y| = 2 \therefore y^{-1} = y ,\ (3)& x^4 = yx^2y = yyx =x\ &\because x \ne e\ &\therefore x^3 = e, |x| = 3. \end{align} $$

证明群/子群¶

注意: 群的四大性质中, 对于同一个运算, 结合性\单位元\任意元素的逆元都是唯一的, 因此如果一个群满足这些条件, 那么显然它的所有元素具有结合律, 每个元素都有逆元, 单位元存在且唯一.

那么, 对于G的子代数H, 我们只需要验证:

满足运算封闭性

(结合律可以说明,但是必然满足)

单位元在H中

任意元素的逆元在H中

证明:若 $H,K$ 是 $G$ 的子群 $$ (1)H\cap K也是G的子群\ (2)H\cup K是G的子群\iff H \sube K \or K\sube H. $$

$Hint.$ 证明利用到集合的交并的性质.

第二问利用反证法,考虑不属于公共部分的两个元素,证明 $hk^{-1}\not \in H\cup K.$

$\text { 假设 } G \text { 是阿贝尔群， } H \text { 是群 } G \text { 中所有阶为有限的元素构成的集合，证明: } H \text { 是子群 }$

依次验证群的四大性质

封闭性: $\forall x, y \in R, <span class="arithmatex"><span class="MathJax_Preview">设</span><script type="math/tex">设$ |x| = a, |y| = b, \because (xy)^{lcm(a,b)} = x^{lcm(a,b)} y^{lcm (a,b)} = e|x| = a, |y| = b, \because (xy)^{lcm(a,b)} = x^{lcm(a,b)} y^{lcm (a,b)} = e,这意味着 $xy$ 的阶也是有限的,且不超过 $lcm (a,b)$ ,注意,这里用到了G是阿贝尔群,意味着这个运算具有交换律,因此才可以得出这个结论,再根据H的定义, $\therefore H \le G$ .

结合律: 由于G是群,H中的元素属于G,因此也满足结合律

单位元: 单位元就是G的单位元,显然也属于H.

逆元:注意到 $\forall a \in H, |a| = r, <span class="arithmatex"><span class="MathJax_Preview">那么对于</span><script type="math/tex">那么对于$ a^1, a^2, \dots , a^{r-1}a1, a^2, \dots , a^{r-1}都为有限阶元,且阶数 $={r\over gcd(i, r)}$ ,因此逆元即 $a^{r-1}$ 也在H中.$\square $

设G是群,a是G中的二阶元,证明G中与a可交换的元素构成G的子群

依次验证群的四大性质:

封闭性: $\forall x,y \in H, ax = xa , ay = ya \Rightarrow axy = xay = xya \Rightarrow xy \in H$

可结合性: 因为H中的元素都属于G,而G是群,G中元素满足结合律,因此H中元素也满足结合律

单位元: 显然单位元e也在H中

逆元: $\because \forall x \in H, x \cdot x^{-1} = x^{-1}\cdot x = e \therefore x^{-1} \in H.\square $

判断是否为循环群¶

几种充分条件:

找到一个元素能够生成这个群

找到一个元素的阶等于这个群的阶

素数阶群一定是循环群

循环群的子群一定是循环群

求陪集¶

一般采用枚举的方法计算H的陪集,以右陪集为例,解题步骤:

计算H对G的指数 $[G:H] = {|G| \over |H|}$
第1个陪集就是 $He =H$
任选元素 $a \in G-H$ ,求陪集,为第2个
任选元素 $b \in G - (H \cup Ha)$ ,求陪集,为第3个

以此类推,由于指数限制,在有限步内求得全部陪集

这里用到 $a \in Hb \iff Ha = Hb$

因此如果已经找到陪集 $Ha$ ,那么接下来就不用在 $Ha$ 中寻找新的陪集,因为如果在 $Ha$ 中任取元素 $x$ , $Hx = Ha$ ,也就是说这样生成的陪集是与刚才相同的.

子群格的结构¶

可以从小到大枚举G的子群,还没有高效的对每个群都适用的枚举算法.可以

写出每个元素的阶

找到由每个元素生成的子群

按照它们的包含关系作成一个偏序结构

对于循环群, 可以保证所有的子群可以由每个元素生成

对于非循环群,求出所有子群的过程会比较艰难

从下到上检查子群的并集,看看它们是否构成新的更大的子群,

如果能,就把它加入到这个偏序结构中

如果不能,就不断向其中加入新的元素直至代数系统封闭,这时就构成群.将其加入偏序结构中.

Lagrange定理(Cauchy定理)的应用¶

这个很重要!

证明6阶群必有3阶元.

分类讨论.

(1)G含有6阶元a,则 $a^2$ 为3阶元

(2)G中不含有6阶元,则由拉格朗日定理推论,若不存在3阶元,则只存在1\2阶元,容易构造H= $\{e,a,b,ab\}$ ,显然H 是G的子群,但是4不是6的因子,矛盾.

证明阶小于6的群都是阿贝尔群.

引理1:由一个元素生成的群都是阿贝尔群.

引理2: $\forall a \in G, a^2 = e \to G 为阿贝尔群.$

分类讨论:

1阶群是平凡的
2,3,5阶群都是素数阶群,由拉格朗日定理,一定存在一个元素使得 $<a> = G$ ,则由引理1可证
4阶群分类
- 含有4阶元,同上
- 不含4阶元,则只含1,2阶元,由引理2可证.
证明20阶群必有5阶元.

这题有点超纲.

[Lagrange定理]对20阶群G可能含有的元素的阶进行分类讨论

若含有20阶元/10阶元/5阶元,则容易找到5阶元,于是可以由其生成5阶子群

若不含以上这些,则一定含有单位元,2阶元, 可能含有4阶元

若不含四阶元,

法1 构造 $H = \{e,a,b,c,ab,ac,bc,abc\},$ 则显然 $H\sub G$ ,但是由Lagrange定理, H的阶数必须是G的因子,矛盾.

法2 证明一个引理: 若一个群只含有1,2阶元,那么这个群的阶数一定是 $2^k$ .则显然矛盾.

这个证明需要用到: 若$\forall x\in G, x^2 = e \to $G是阿贝尔群.

于是我们可以证明: 对于G的任意两个不同的元素,它们的乘积也是2阶元.( $\forall x, y, \in G, (xy)^2 = x^2y^2 = e$ )

于是问题转化为求G的所有不重复的乘积,不难发现所有的2阶元数等于 $(\sum_{i = 1}^{n} C_n^i)$ .由二项式定理, $|G| = 2^n, n$ 为所有*最初的元素*个数.例如 $H = \{e,a,b,c,ab,ac,bc,abc\}$ ,其中除了单位元都是2阶元.

设 $H_1,H_2$ 分别是G的 $r,s$ 阶子群,且r,s互素,证明: $H_1\cap H_2 = \{e\}.$

引理: $H_1 \cap H_2$ 也是G的子群. $$ Pf.\ 记|H_1\cap H_2| = x. \because H_1\cap H_2 \le H_1\ \therefore x | r\ 同理, x|s\ \Rightarrow x | gcd(r,s) = 1\ \Rightarrow x =1.\square $$

代数系统-群与环¶

知识点¶

群的定义¶

典型的群¶

元素的幂 k阶元¶

幂的运算性质¶

群的性质¶

消去律¶

元素的性质¶

子群¶

判定定理¶

由元素a生成的子群¶

由B生成的子群¶

子群格¶

群的分解¶

陪集¶

右陪集的性质¶

右陪集的划分¶

正规子群(不变子群)¶

左右陪集的关系¶

Lagrange定理¶

Cauchy定理¶

循环群¶

定义¶

求所有生成元¶

求循环群的所有子群¶

置换群¶

置换作为运算¶

置换作为群¶

元素的阶¶

Cayley 定理¶

环与域¶

习题¶

群的性质¶

证明元素的阶相同 求元素的阶¶

证明群/子群¶

判断是否为循环群¶

求陪集¶

子群格的结构¶

Lagrange定理(Cauchy定理)的应用¶

证明元素的阶相同求元素的阶¶