格🤣与布尔代数¶

抽象代数学习笔记（十） - 知乎 (zhihu.com)

Distributive Lattice - YouTube

知识点¶

格与布尔代数是具有**两个**二元运算的代数系统

格¶

定义¶

设 $<S,\le >$ 是偏序集,如果 $\forall x, y \in S, \{x,y\}$ 都有**最小上界**和**最大下界**,则称S关于偏序$\le $ 作成一个格.

因此可以定义运算:

$x\and y$ 表示最大下界
$x\or y$ 表示最小上界

格的对偶原理¶

将 $\le \iff \ge$ 对换, $\and \iff \or$ 对换,得到**对偶命题**

$f <span class="arithmatex"><span class="MathJax_Preview">与对偶命题</span><script type="math/tex">与对偶命题$ f^*f*对一切格具有相同的真值.

格的性质¶

运算 $\and ,\or$ 满足
交换律
结合律
幂等律
吸收率
$a \le b \iff a\and b = a \iff a\or b = b$ .

注:这里 $\le,\ge$ 并不是一种运算,而是偏序集S自带的**关系符号**,表示a是b的**下界**.

分配不等式 $a \or (b\and c) \le (a\or b) \and (a\or c)$

格的运算¶

$1)& x\and y\quad \le \quad x,\ y\quad \le \quad x\or y\\ 2)& m \le x \and m \le y \rightarrow m \le x\and y\\ 3)& x\le m \and y \le m \rightarrow x\or y \le m$

格的代数结构定义¶

对于运算 $\and, \or$ ,满足

封闭性
交换律
结合律
吸收率
(幂等律)

注:幂等律可以由前面几项推出.因此不需证明,也是应该满足的.

分配格¶

满足分配率的格叫做分配格

分配格的充要条件¶

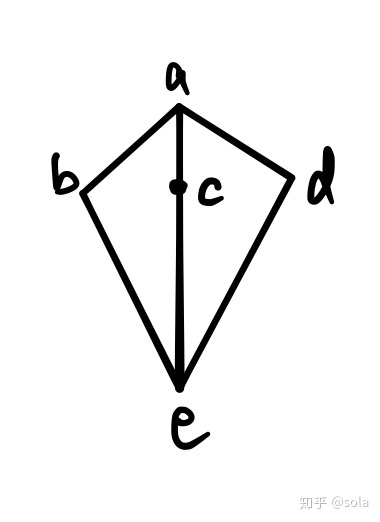
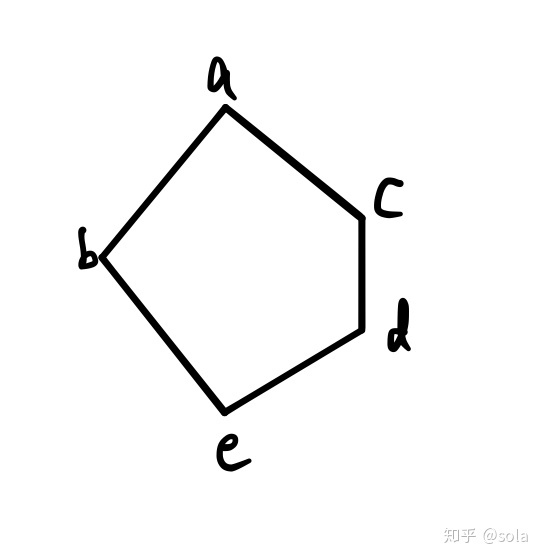
格L是分配格当且仅当L中不含有与**钻石格**或**五角格**同构的子格.

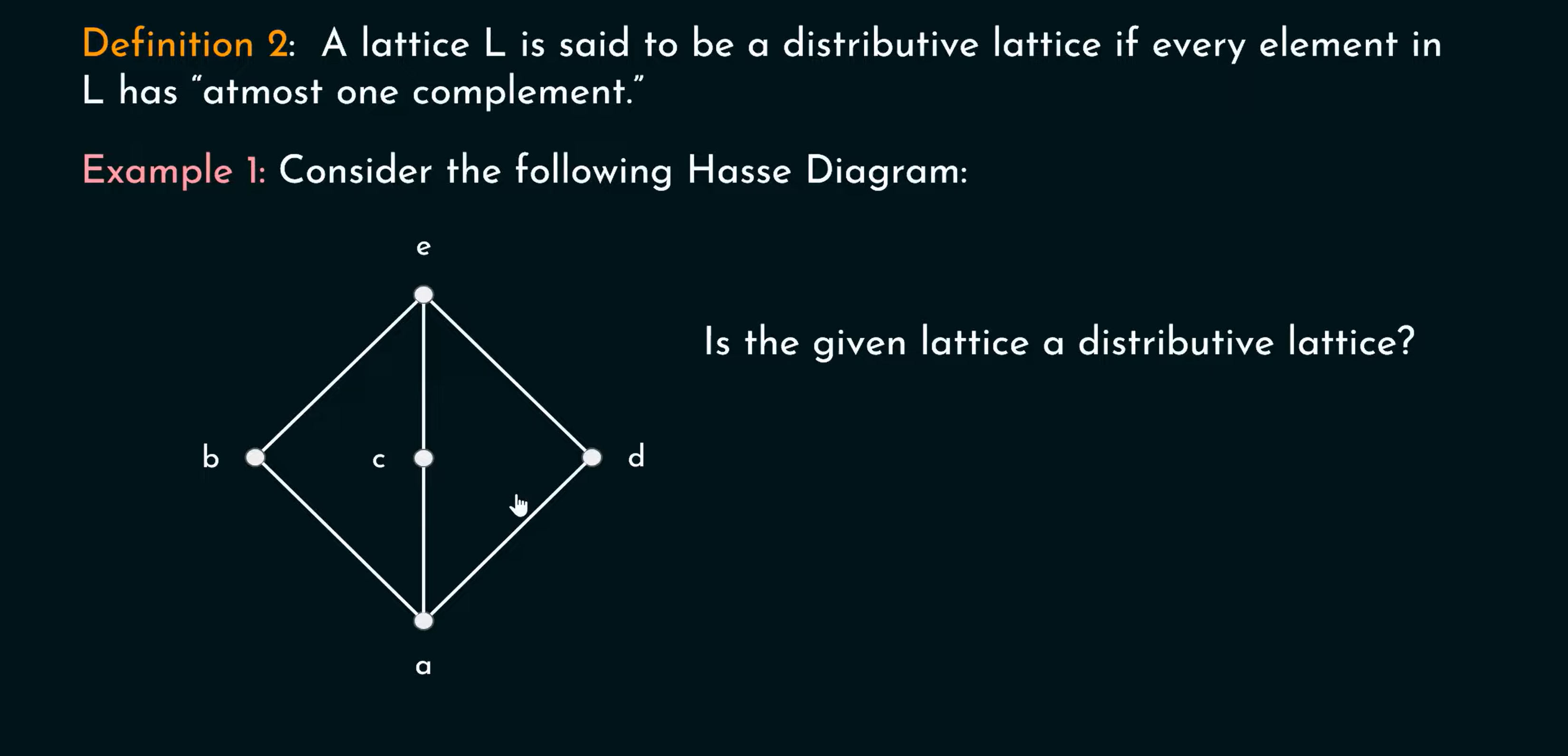
格L是分配格当且仅当每个元素有至多一个补元.

推论

小于5元的格都是分配格
任何一条链都是分配格

问题: 含不含五角格?

有补格¶

有界格¶

格L中若含有**全下界**和**全上界**,则称L为**有补格**.记作 $L = <S, \and ,\or,0,1>$ .

有限格都是有界格. $0= a_1\and a_2 \and \dots \and a_n$ .

补元¶

$a \and b = 0, a \or b = 1$ .则a与b互为补元.一个元素补元可以有0,1,或多个.

(有界)分配格的补元若存在,则唯一.

若每个元素都有补元,则称L为**有补格**.

布尔代数¶

若一个格是**有补分配格**,则称它为**布尔格**或**布尔代数**.

布尔代数中,每一个元素有且仅有一个补元.顾可以把*求补元*看做一种一元运算.因此布尔格可记作 $<B,\and, \or, ', 0,1>$ .

典型的布尔代数¶

$<S_{110,\gcd, lcm}>$ ,S表示110的所有正因子
$<P(B),\cap, \cup, \sim, \empty, B>$
数理逻辑中的逻辑代数也是布尔代数.
数字电路中的逻辑代数也是布尔代数.

布尔代数的性质¶

$(a')' = a$ (双重否定律)
$(a\and b)' = a' \or b'$ (De Morgan's Law)

布尔格的代数系统定义¶

封闭性
交换律
分配率
两个运算都有单位元(同一律)
有补元(补元律)
(吸收律)
(结合律)

注: 如果从代数系统的角度来审视

$\and, \or <span class="arithmatex"><span class="MathJax_Preview">作为两种运算,它们的单位元分别为</span><script type="math/tex">作为两种运算,它们的单位元分别为$ 1,01,0,零元分别为 $0,1$

原子¶

习题¶

判断是否构成格¶

比较的时候只需要比较两个**不可比**的元素.(可比的元素必然有最大下界和最小上界)

注意:两个元素**不可比**,是指在哈斯图中不存在一条连通两个元素的通路.

要求任意两个元素的上界和下界元素都是**可比**的,因此才能找到最小上界和最大下界.

证明格相关的等式¶

往往利用偏序的反对称性: $a\le b \and b \le a \to a = b$ .