微积分复习笔记

5 多元函数微分学

5.1 多元函数的极限与连续性

5.1.1 点集的基本性质

考虑n维空间下点的性质，以描述n空间的性质

• 距离的量度$\rho=\sqrt {(a_i-b_i)^2}$

• 邻域 $N_\delta(P_0)$

• 去心邻域 $\mathring{N}_\delta(P_0)$
• 内点：G的内面的一个点走一个足够小的距离，仍然在内面
• 内部$G^o$：内点的集合
• 问题：“G的内点”和“属于G”的区别？
  • 属于G，可能为G的内点或边界点
• 外点：G的外面的一个点走一个足够小的距离，仍然在外面
• 外部：外点的集合
• 边界点$\partial G$：走一个任意大小的距离，都有邻域中的部分点为内点，另一部分为外点
• 聚点：对于任意大小的 去心邻域 中，总有点属于G
• 问题：数列中的聚点为子数列的极限 ？
• 问题：聚点是什么？
• 开集：G中所有的点都是G的内点，即G的内部 == G
• 开集一定不包含边界点。
• 闭集：全集对开集的补集就是闭集。即，闭集外的点，走任意小的距离，仍然在闭集外。
• 闭集一定包含边界点。
• 归纳：$<span class="arithmatex"><span class="MathJax_Preview">R^n = E^o \cup \partial E \cup (E^c)^o \\ 开集: E = E^o \\ 闭集： E = E^o \cup \partial E \wedge E^c = (E^c)^o</span><script type="math/tex">R^n = E^o \cup \partial E \cup (E^c)^o \\ 开集: E = E^o \\ 闭集： E = E^o \cup \partial E \wedge E^c = (E^c)^o$
• 连通集：G内任意两点都可以被一条曲线连接，且该曲线上的点都属于G。
• 开区域：开集+连通集
• 空集是开区域
• 闭区域：非空 开区域+边界
• 问题：为什么定义为：闭集+连通集？
• 区域：开区域、闭区域
• 空集和全空间既是开集，又是闭集
• 有界集
• 直径：$d(G) = sup{\{\rho(P_1, P_2)|\forall P_1,P_2 \in G\}}$
• 无界集

关于集合论的阅读：请问开集和闭集如何理解？ - sola的回答 - 知乎 https://www.zhihu.com/question/378515815/answer/1071427708

5.1.2 多元函数的概念

5.1.3 多元函数的极限

二重极限

• $P_0(x_0, y_0)$为D的 聚点 ，$\epsilon-\delta$语言
• $0 < \sqrt{(x - x_0)^2 + (y- y_0) ^ 2} < \delta$

• $ |f(x, y) - A| < \epsilon$

• 证明/求二重极限的方法：

  • 定义法：配方/放缩$\rightarrow$凑$\rho$
  • 若函数在该点连续且极限存在，则可以直接带入得到答案。
  • 对于不定型：夹逼/局部有界性。
  • 注：对于极限为0的证明，可以任意添加或去除绝对值符号。可以据此进行放缩/夹逼。

• 二重极限的复杂性在于点P在平面上趋近$P_0$的方式是多重多样的。（一重极限的趋近方式只有左极限 | 右极限）

• 判定二重极限不存在的方法：找到两种趋近$P_0$ 的方式，使得$f(x,y)$趋近不同的值（包括极限不存在）。

累次极限

5.1.4 多元函数的连续性

连续性定义

$设Ｇ\subseteq G,函数f在G上有定义，P_0是G的$聚点（边界点/内点）$, 且P_0\in G, 若 \displaystyle\ \lim_{P \to P_0} = f(P_0)$,则函数在$P_0$处连续。

• 若处处连续，则在G上连续。
• 等价定义：$\Delta z \rightarrow 0(\Delta x \rightarrow 0, \Delta y \rightarrow 0)$
• $f(x,y)在(x_0, y_0)处关于x连续$：固定$y = y_0$，一元极限。

连续性的性质（都是在==有界闭区域==条件下）

• 零点定理
• 介质定理
• 有界性定理
• 最值定理

5.2 偏导数与全微分

5.2.1 偏导数

定义

$函数z = f(x, y)在点(x_0, y_0)处对x的偏导数，记作\\{\partial f \over \partial x}(x_0, y_0)$

• 偏导数都存在（未必相等），则函数在该点可偏导。偏导数存在，说明左偏导数=右偏导数。

可偏导和连续的关系

• 回顾：一元函数：

$可导\implies连续 \ \lim_{\Delta x\rightarrow0}{f(x+ \Delta x) - f(x)\over\Delta x} = A \implies \lim(f(x+\Delta x) - f(x)) = \lim(A\Delta x+o(\Delta x)) = 0(\Delta x\rightarrow 0)\连续 \not\Rightarrow 可导\ 左导数 \neq 右导数 or 左/右导数可能不存在f(x) = {1\over x} 在x = 0处 $

• 多元函数在某一点可偏导$\not\Rightarrow $在这一点连续。

• $$Thm. 函数在点P的某邻域内可偏导，且偏导数在该邻域内有界，则函数在P处连续\\Pf.插入中间量，使用微分中值定理$$

• 

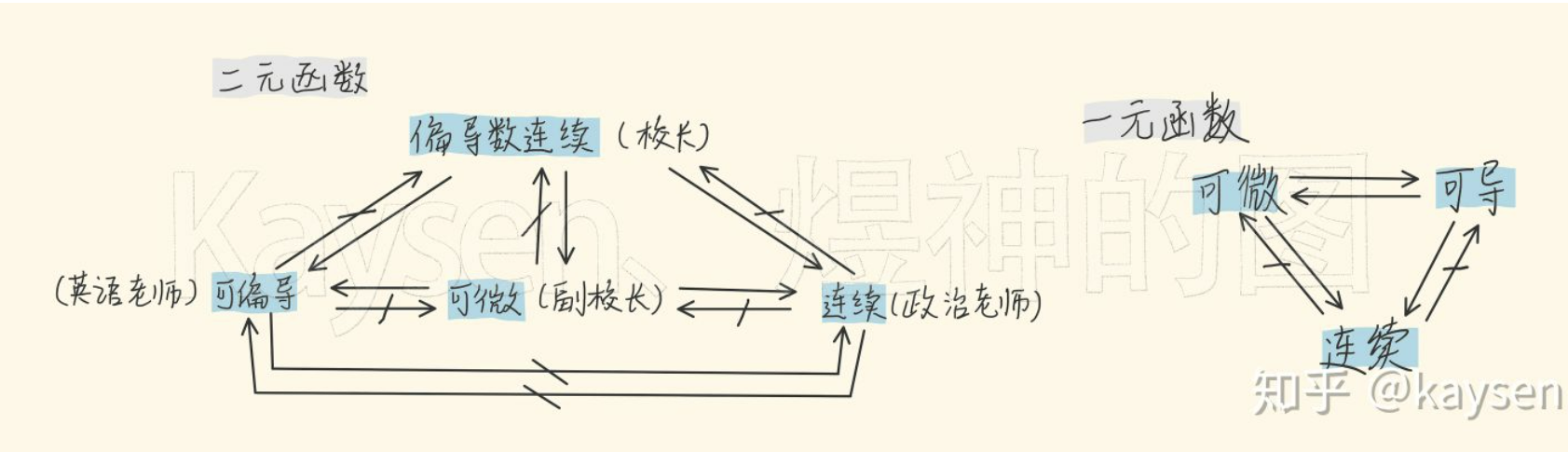
• [参考资料]二元微分：连续、可微、可偏导、偏导连续的超强通俗解析！ - kaysen学长的文章 - 知乎 https://zhuanlan.zhihu.com/p/331732466

5.2.2 高阶偏导数

混合偏导数与求导次序无关的充分条件

• $$Thm.若二阶混合偏导数f''_{xy}(x,y)与f''_{yx}(x,y) 在 (x,y)处连续，则f''_{xy}(x,y) = f''_{yx}(x,y) \\Pf.运用拉格朗日中值定理$$

5.2.3 全微分

概念

• 用全微分$dz$代替全增量$\Delta z$来研究函数$f(x,y)在(x,y)$附近的变化情况

• $\Delta z = A \Delta x + B\Delta y + o(\rho), \rho = \sqrt{(\Delta x)^2 +(\Delta y)^2}$

• 连续和可偏导是可微的必要条件（容易证明），但不是充分条件。
• 我的理解：
• 一元可微（可导）：线性表示曲线（用一条小直线近似该点处的曲线，忽略非线性项）
• 二元可微：线性表示曲面（用一个小平面近似该点处的曲面，忽略非线性项）

证明可微的方法

• 一个充分条件：
• $Thm. 函数z = f(x,y)在(x,y)的某个邻域内可偏导，且f'_x(x,y),f'_y(x,y)在(x,y)处连续，则函数在该点可微$
• 做题常用：$证明{\omega\over\rho}\rightarrow 0(\rho \to 0^+),\omega = f(x+\Delta x, y+\Delta y)- f_1'(x,y)\Delta x - f_2'(x,y)\Delta y- f(x,y)$

连续可微

• 若函数在点P的某邻域内可偏导，且**偏导数在该点都连续**，则称函数在该点连续可微（可以推广到整个开区域G）

• 联系：一元函数：连续可导，指导函数连续

5.3 复合函数与隐函数的偏导数

5.3.1 复合函数的偏导数

链式法则

一阶全微分的形式不变性

复合函数的高阶偏导数

注意到一般性质比较好的函数的混合高阶偏导数（都连续）是相等的。即，$f''_{xy}(x,y) = f''_{yx}(x,y)$

5.3.2 隐函数的偏导数

由一个方程确定的隐函数

• 二元函数

$$Thm.1.\ let\ P(x_0,y_0)\in \R^2, G = N_\delta(P_0),if\\ 1)函数F在G上连续可微\\ 2)F(P_0)=0\\3)F'_y(P-0) \neq 0\\ then\exist! y = f(x),s.t. \\ f连续可微，且在一个邻域内f'(x) = -{F'_x(x,y)\over F'_y(x,y)}\\Pf.\ let\ g(x) = F(x, f(x))= 0\\对g求导恒为零\\\Rightarrow F_1' + F_2'\cdot f' = 0 \\ \Rightarrow f' = -{F_1'\over F_x'}$$

• 三元函数

$$Thm.2.\ for\ F(x, y, z) = 0, \exist!z = f(x,y),s.t. \\Pf. \ let g(x,y) = F(x, y, f(x,y)) = 0.\\\because g(x,y)为常值函数,g'_x(x,y) = g_y'(x,y)恒为零\\ \therefore g_x' = {\partial F\over \partial x} + {\partial F \over \partial z}\cdot {\partial f\over \partial x} = 0 \\ \Rightarrow {\partial f\over \partial x } = -{F_1'\over F_3'}$$

由方程组确定的隐函数

$$1)\ F(x,y,u,v) = 0\\2)\ H(x,y,u,v) = 0 \\let \ f(x,y) = F(x,y,u(x,y),v(x,y)) = 0 \\ h(x,y) = H(x,y,u(x,y),v(x,y)) = 0 \\then \ f_1' = F_1' + F_3'\cdot u_1' + F_4'\cdot v_1' = 0\quad (1)\\ g_1' = H_1' + H_3'\cdot u_1' + H_4' \cdot v_1' = 0\quad (2)\\ by (1)(2),\Rightarrow \\ \begin{pmatrix}F_3' & F_4'\\ H_3'& H_4' \end{pmatrix}\cdot \begin{pmatrix}u_1'\\ v_1' \end{pmatrix} = \begin{pmatrix} -F_1' \\ -H_1' \end{pmatrix} \\ by\ Cramer\ Rule\ you\ can\ solve\ it$$

5.4 二元函数的泰勒公式

5.5 多元向量函数

5.6 偏导数在几何上的应用

5.6.1 空间曲线的切线与法平面

• 形象理解：切向量就是速度矢量，法平面就是垂直于切向量的平面（即法平面的法向量为切向量）
• 情形一：参数化
• $let\ x = \varphi(t), y = \psi(t), z = \omega(t),\\ 显然切向量为(\varphi'(t), \psi'(t), \omega'(t))$
• 情形二：一般式（即两曲面相交得到曲线）
• ${\begin{cases}F(\varphi(t),\psi(t),\omega(t)) = 0\\ H(\varphi(t),\psi(t),\omega(t)) = 0 \end{cases}}\\ 对于两个平面，尝试分别对t求导\\ {dF\over dt} = F_1'\cdot \varphi' + F_2'\cdot \psi'+F_3'\cdot \omega' = 0 \\ \iff (F_1', F_2', F_3') \cdot (\varphi',\psi',\omega') = 0\\ then\ we\ find\ \vec{n_1} \cdot \vec{v} = \vec{0} \\ similarly\ we\ have\ \vec{n_2} \cdot \vec{v} = \vec{0}\\ then\ \vec{v}\ can\ be\ \vec{n_1} \times \vec{n_2}$

5.6.2 空间曲面的切平面与法线

• 个人感觉切平面和微分的关系很大
• 情形一：参数化-一元参数t
• $$对于F(x,y,z) = 0,考虑过该点的任一条曲线\\ x = \varphi(t), y = \psi(t), z = \omega(t),\\ then,F(\varphi(t),\psi(t),\omega(t)) = 0\\\Rightarrow {dF\over dt} = F_1'\cdot \varphi' + F_2'\cdot \psi'+F_3'\cdot \omega' = 0 \\ \iff (F_1', F_2', F_3') \cdot (\varphi',\psi',\omega') = 0\\ then\ we\ find\ (F_1', F_2', F_3') \cdot \vec{v} = \vec{0}\\\because \forall t,即曲线任取,\\ \therefore \vec{v}可以沿该曲面上的任意方向，都与(F_1', F_2', F_3')垂直,\\ \therefore\nabla F = (F_1', F_2', F_3') = \vec{n}.$$
• 情形二：参数化-二元参数u, v
• $$F(x(u,v),y(u,v),z(u,v)) = 0\\ 对u,v求偏导\\ {\begin{cases} F_1'\cdot x_1' + F_2'\cdot y_1' + F_3'\cdot z_1'= 0\\ F_1'\cdot x_2' + F_2'\cdot y_2' + F_3'\cdot z_2'= 0\end{cases}}\\ so\ (F_1',F_2',F_3')\cdot (x_1',y_1',z_1') = 0\\ (F_1',F_2',F_3')\cdot (x_2',y_2',z_2') = 0\\ so\ \vec{n}\ can\ be\ (x_1',y_1',z_1')\times (x_2',y_2',z_2')$$

5.7 极值与条件极值

5.7.1 二元函数的极值

驻点：偏导数都为0

可疑极值点（驻点+不可偏导的点）

求极值点

• $$Thm.\ G = N_\delta(P_0),f在G内二阶连续可微(二阶偏导连续),且f'_x = f_y' = 0,\\ let\ A = f_{xx}'', B = f_{xy}'', C = f_{yy}''\\ 1)B^2-AC < 0, A>0\Rightarrow f(P)取得极小值\\ 2)B^2-AC < 0 ,A < 0\Rightarrow 取得极大值\\ 3) B^2-AC > 0\Rightarrow f(P)不是极值\\ 4)B^2-AC = 0\ or B^2-AC < 0 \and A = 0 \Rightarrow 无法判断，需单独讨论\\ Pf(略)$$

• 定理的应用：

• 对形如$f(x,y)$求极值

• 直接求偏导，根据$f_1' = f_2' = 0$得到驻点

• 据此进一步求出$f_{11}'',f_{12}'',f_{22}''$，对每一个驻点讨论$B^2-AC,A$的符号

• 若有特殊情况，单独讨论

• 对由形如$F(x,y,z) = 0确定z = f(x,y)$的隐函数求极值

• 改写成$F(x,y,f(x,y))$的形式，求偏导，得到两个方程（1），令$f_1' = f_2'= 0$，得到两个关于x,y,z的方程（2），（2）与原方程联立，得到具体的驻点。

• 对得到的两个方程（1）进一步求偏导（高阶偏导数的求法），得到三个方程，代入$f_1' = f_2' = 0,x_0,y_0,z_0$，据此求解具体的A、B、C，讨论极值。
• 注：也可以直接显式求出偏导表达式（不过可能形式比较复杂），然后同1.

5.7.2 最大值与最小值

一般方法

函数$f(x,y)$，对于有界闭区域D，

• 求出所有D内的驻点对应的函数值
• 求出在$\partial D$上的最大值、最小值

5.7.3 条件极值

定义：$F(x,y,z)$在约束方程$\varphi(x,y,z) = 0$下的极值

方法一：消元法

转换为$F(x,y,z(x,y))$的二元函数的求极值问题

问题：通常不好根据$\varphi$转化为$z = z(x,y)$

方法二：拉格朗日乘数法

• 三元函数求条件极值

$Thm.\ 设f(x,y,z)连续可微,函数\varphi(x,y,z)连续可微,且\varphi_z'\neq 0,\\ 函数f(x,y,z)满足约束方程\varphi(x,y,z)的条件极值在点P_0(x_0,y_0,z_0)处取得,\\ let\ F(x,y,z,\lambda) = f(x,y,z) + \lambda \varphi(x,y,z)\\ then \nabla F = \vec{0}\\ i.e.{\begin{cases} F_1' = 0\\ F_2' = 0\\ F_3' = 0\\ F_4' = 0 \end{cases}}\\ Pf. 作简单说明:\\ 1)\varphi视作等高面,\\ 在等高面，有\nabla \varphi \bot切平面i.e.\nabla \varphi//\vec{n}\\ 2)f在该点沿其切平面内任意向量方向前进，值都不能变化，\\ 故\nabla f\bot 切平面i.e.\nabla f// \vec{n}\\ 3)该点在切平面C:\varphi(x,y,z) = 0上$

• 式中$F为拉格朗日函数，\lambda为拉格朗日乘数$

• 推广：如果有多个约束方程，那么建立拉格朗日方程形如$F(x,y,z,\lambda,\mu), \nabla F = \vec{0}$

• 条件极值与方向向量（二元函数求条件极值）

• 我们现在考虑二元连续可微函数$f(x,y)$限制在曲线C : g(x, y) = 0 上 的取值情况。我们称$P_0$ = (a, b) 为条件极值点，如果∀P ∈ C, f(P) ≥ f($P_0$) 或者∀P ∈ C, f(P) ≤ f($P_0$)。其中P = (x, y) ∈ C 的涵义等价于g(x, y) = 0。 假设我们站在极值点$P_0$，考虑行径方向$l$（一共有两个方向：前进，后 退）。若${\partial f\over \partial l}(P_0)>0$, 则预示着我们往$l$方向前进（更准确地说，我们需要 一边走一边调整方向，以保持我们始终在C 上），可以看到$f$取值增加， 往$l$的反方向前进，我们会看到$f$的取值减小，因此$P_0$不会是极值点；若${\partial f\over \partial l}(P_0)<0$, 则预示着我们往$l$ 方向前进，可以看到$f$取值减小，往反方向 前线，则f 取值增加，因此$P_0$ 不会是极值点。于是，我们只有剩下的一种可能:${\partial f\over \partial l}(P_0)=0.\ i.e.\nabla f \bot l$

• 因为行径方向和$C:g(x,y) = 0$在$P_0$点切向量同向或反向，因此也有$\nabla g\bot l$

5.8 方向导数

定义

$<span class="arithmatex"><span class="MathJax_Preview">f在P=(a,b)沿l方向的方向导数为\\ {\partial f\over \partial l}(P) =\displaystyle \lim_{t \to 0^+}{f(P+tl)-f(P)\over t}</span><script type="math/tex">f在P=(a,b)沿l方向的方向导数为\\ {\partial f\over \partial l}(P) =\displaystyle \lim_{t \to 0^+}{f(P+tl)-f(P)\over t}$

等高线

等高线$f(x,y) = k$的切向量与$\nabla f$垂直

方向向量与梯度的关系

• $Thm. let\ |l| = 1,then\\ {\partial f\over \partial l}(P) = \nabla f\cdot \vec{l}= |\nabla f(P)|\cos\theta$

• 假设$\nabla f(P)\neq 0$。易知，若$l$与$\nabla f$ 同方向，则方向导数取到最大 值；若反方向，则取到最小值。

• 假设我们站在点P, 并且沿$l$方向移动。如果该方向的方向导数> 0, 我们预期看到$f$的取值会变大；若< 0, 取值会变小；若= 0, 取值不会变（更准确地说，我们需要一边移动一边随时调整方向，保证方向导数一值为0 才可以）。