题型总结及注意事项¶

题型总结¶

求微分 ${\partial z\over \partial x}$ 类型¶

显式¶

隐式¶

$\text { 4. 设 } x=e^{u} \cos v, y=e^{u} \sin v, z=u v ,\\\text { 求 } \frac{\partial z}{\partial x}, \frac{\partial^{2} z}{\partial x \partial y} \text {. }$

链式法则的运用

已知全微分，求一个原函数¶

要么直接看出来
要么逐次积分

求切线方程、法平面方程¶

求方向导数¶

$||\vec{l}||$ 注意要单位化！

判断连续性、可偏导性、连续性（一致连续性）¶

一致连续性： $<span class="arithmatex"><span class="MathJax_Preview">f_x'(x,y),f_y'(x,y)在(x,y)</span><script type="math/tex">f_x'(x,y),f_y'(x,y)在(x,y)$ 处连续
遇到复杂情况：
洛必达（灵活使用）
夹逼、放缩

求极值（条件极值）¶

Lagrange方程求出可疑极值点不要轻易舍去，想清楚！！

累次积分、二重积分、三重积分¶

遇到绝对值要先去掉
注意累次积分和二重积分的转换
交换积分顺序

计算围成曲面面积、立体体积¶

简化计算：轮换对称性、奇函数、带入方程，简化 $f(x,y,z)$
利用对称性缩小研究的区域
看清楚题意求的是哪一部分的面积是谁被谁截下的面积！！
求曲面面积的办法：
投影法： $z=f(x,y)$ 投影到 $xOy$ 平面同时消去z得到积分区域
对于柱面，可用第一类曲线积分

第一类曲线积分¶

一般换元，化为一元积分

第二类曲线积分¶

Green公式
注意使用条件：非奇点（否则要“挖掉”）
注意**积分方向**：正向曲线
求完了看一下求的是哪一部分，不要答非所问

注意事项¶

$\sqrt{1-\sin^2{x}} = |\cos x|$ ，注意积分的区域，比如 $\int_0^\pi$ 需要拆分！！不然可能最后比答案少项！！
$\text { 10. 求第一类曲线积分 } I_{4}=\oint_{C}(x+y) \mathrm{d} s \text {, 其中 } C \text { 为双纽线 }\left(x^{2}+y^{2}\right)^{2}=2\left(x^{2}-y^{2}\right) \text { 的右半分支. }$

注：换元要注意范围！！

雅各比行列式注意不要求倒！！同时注意可以倒着求。
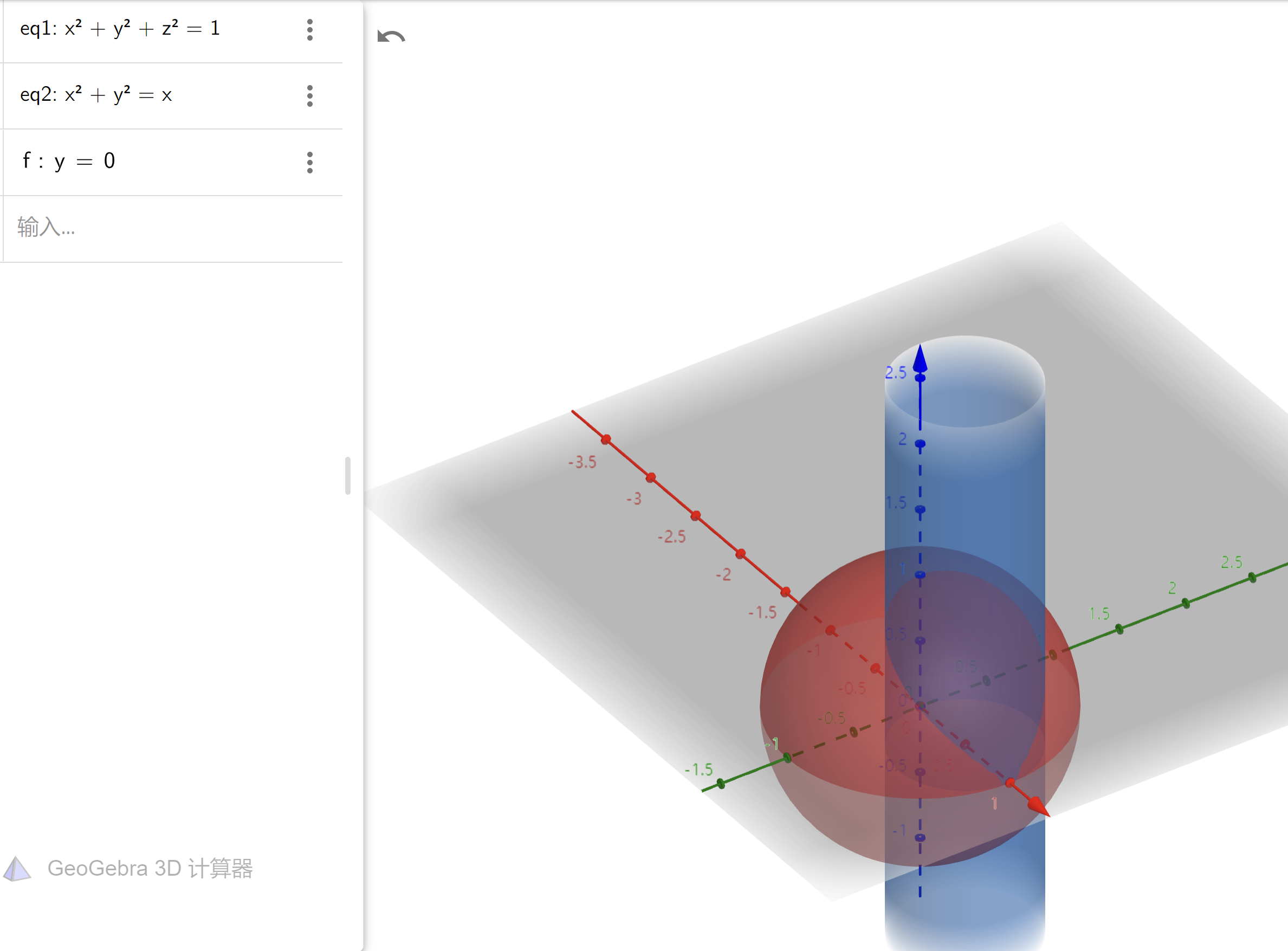
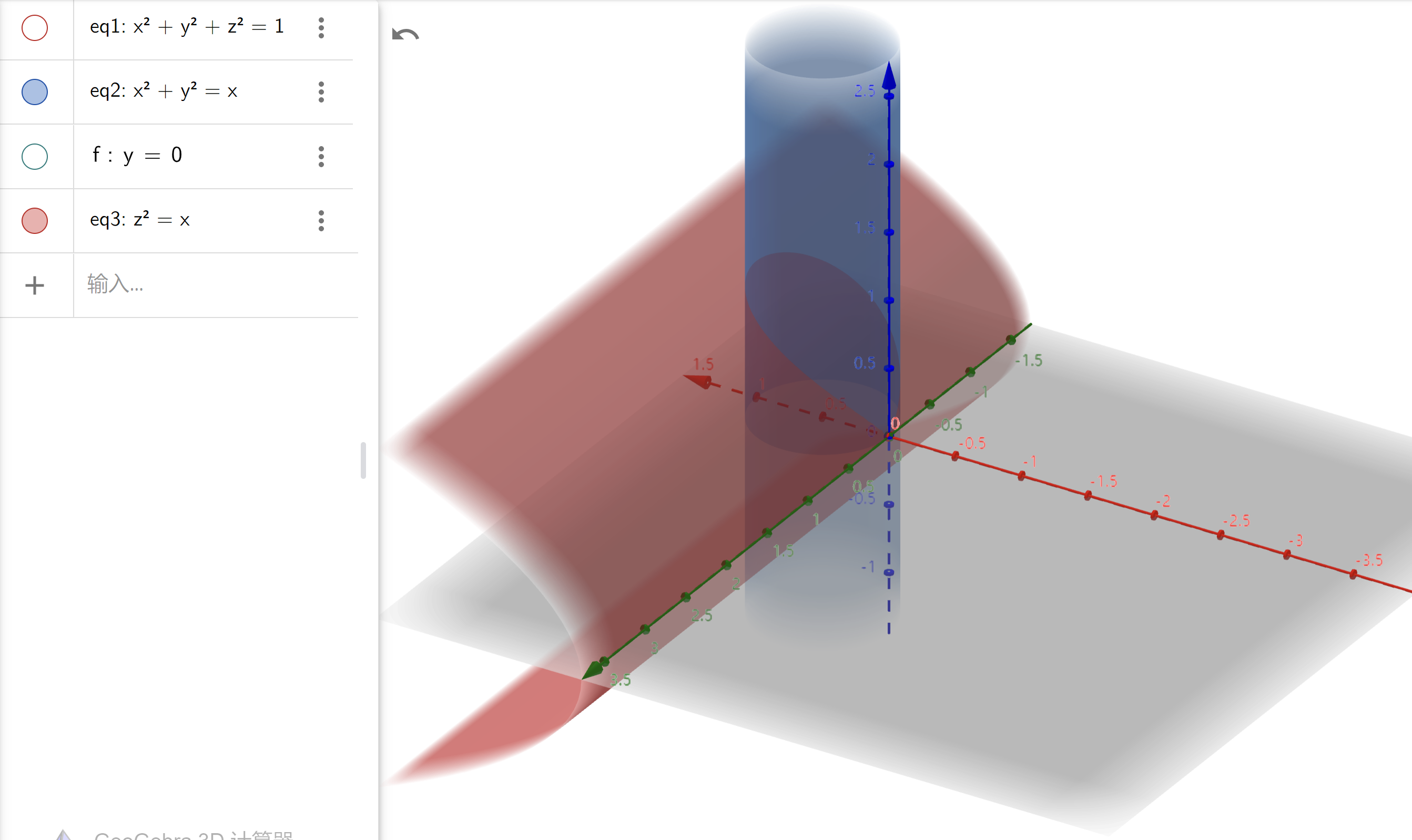
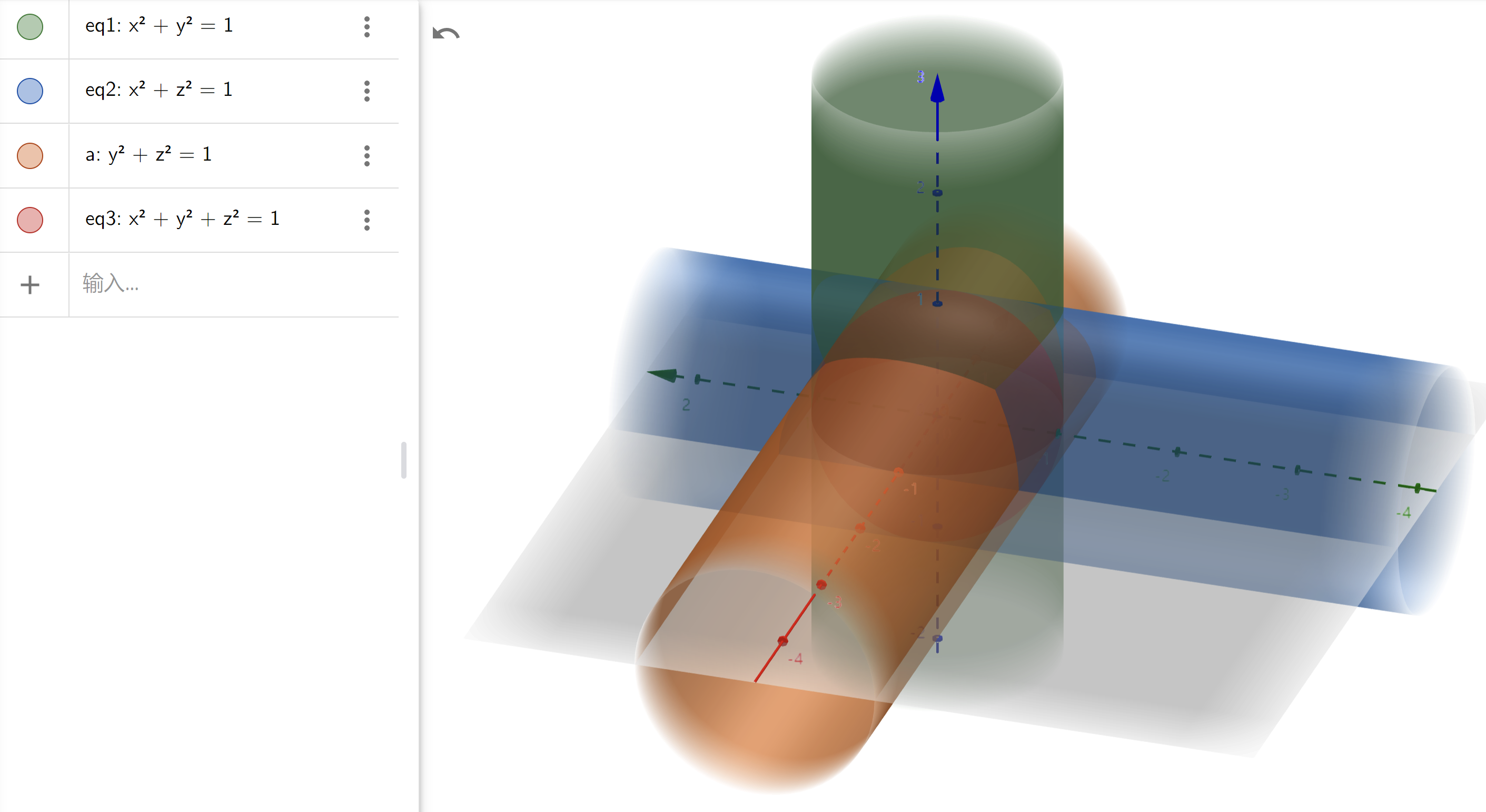
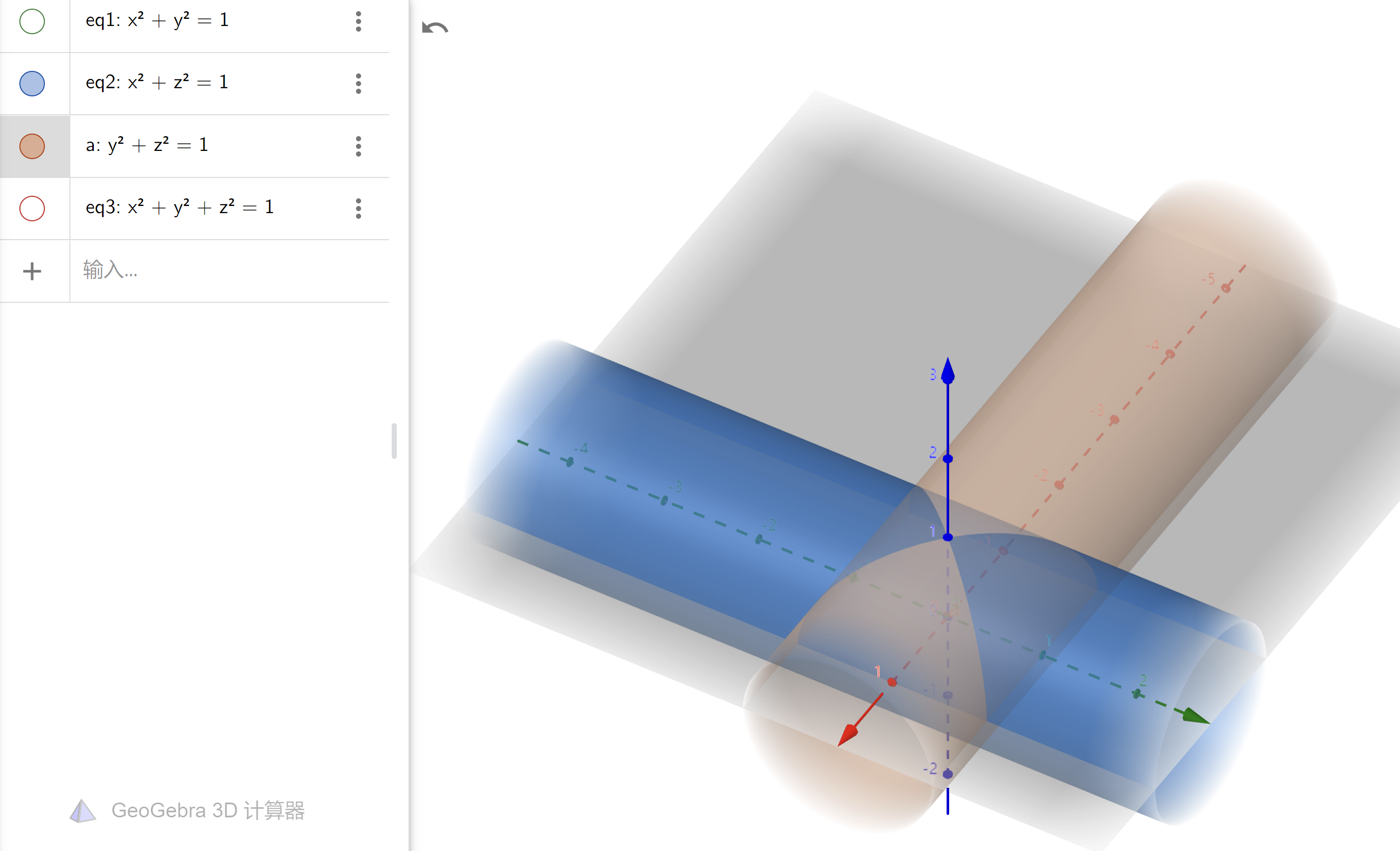
复杂的曲面相交：大胆猜测为圆：圆可以写成球方程和平面方程联立的形式
注意所求区域是不是上下都有不要只求一半！！