不得不说, 计算机系开设的普物实在是太水了...几近高中难度
笔记整理的比较混乱 大概属于是电子垃圾了
普通物理 期末复习¶
考试范围¶
-
力和运动 √
-
运动的守恒量和守恒定律 √
-
刚体和流体的运动 √
牛顿定律、惯性力、动量定理及守恒律、角动量定理及守恒律
功、能、势、动能定理、机械能守恒律、等刚体转动定律、刚体的动能定理、角动量定理等
流体不考
-
相对论基础 -
气体动理论 √
麦克斯韦速率分布律 气体内能等
- 热力学基础 √
考察基本概念: 热力学第一定律\热力学第二定律\理想气体物态方程\卡诺定理\熵的定义等等
- 静止电荷的电场 √
7-1~7-7 + 7-10 库仑定律、电场的高斯定理、环路定理、电场力做功、电势、静电场中的导体，电容、静电场的能量等、 其它节不考
- 恒定电流的磁场 √
第8-1到8-5节，电流、磁场、毕萨定律、高斯定理和环路定理，带电粒子的运动等、其它节不考
- 电磁感应 电磁场理论 √
第9-1到9-3节，例：法拉第电磁感应定律、动生电动势、感生电动势等、其它节不考
复习以课件PPT为纲，重点关注PPT里面例题以及课后作业题
课堂PPT复习¶
质点运动学与动力学¶
求v(t), v(x)类型¶
- 从m\displaystyle{dv\over dt} = \sum F_i入手
- 如果方程形如F(v', x),则做一步转化\displaystyle {dv\over dt} = {dv\over ds}\cdot v
- 如果方程形如F(v',\theta),则做一步转化\displaystyle {dv\over dt} = {dv\over d\theta}\cdot \omega = {dv\over dt}\cdot{v\over l}
- 解完要带入初值条件
自然坐标系¶
$$
\vec{v} = s'\vec{e_\tau}, v = \dot{s}\
{d\vec{e_\tau}\over dt} = |\vec{e_\tau}|\dot{\theta}\vec{e_n} = \dot{\theta}\vec{e_n}\
\because \rho = {ds\over d \theta}\
\therefore \vec{a} = \ddot{s}\vec{e_\tau} + \dot{s}{d\theta \over ds}{ds\over dt}\vec{e_n} = \ddot{s}\vec{e_\tau}+ {v^2\over \rho}\vec{e_n}.
$$
极坐标系¶
难点在于\displaystyle {d{\hat{\rho} }\over dt} = \dot{\theta}\hat{\theta}, {d\hat{\theta}\over dt} = -\dot{\theta}\hat{\rho}的推导.尤其是后者.
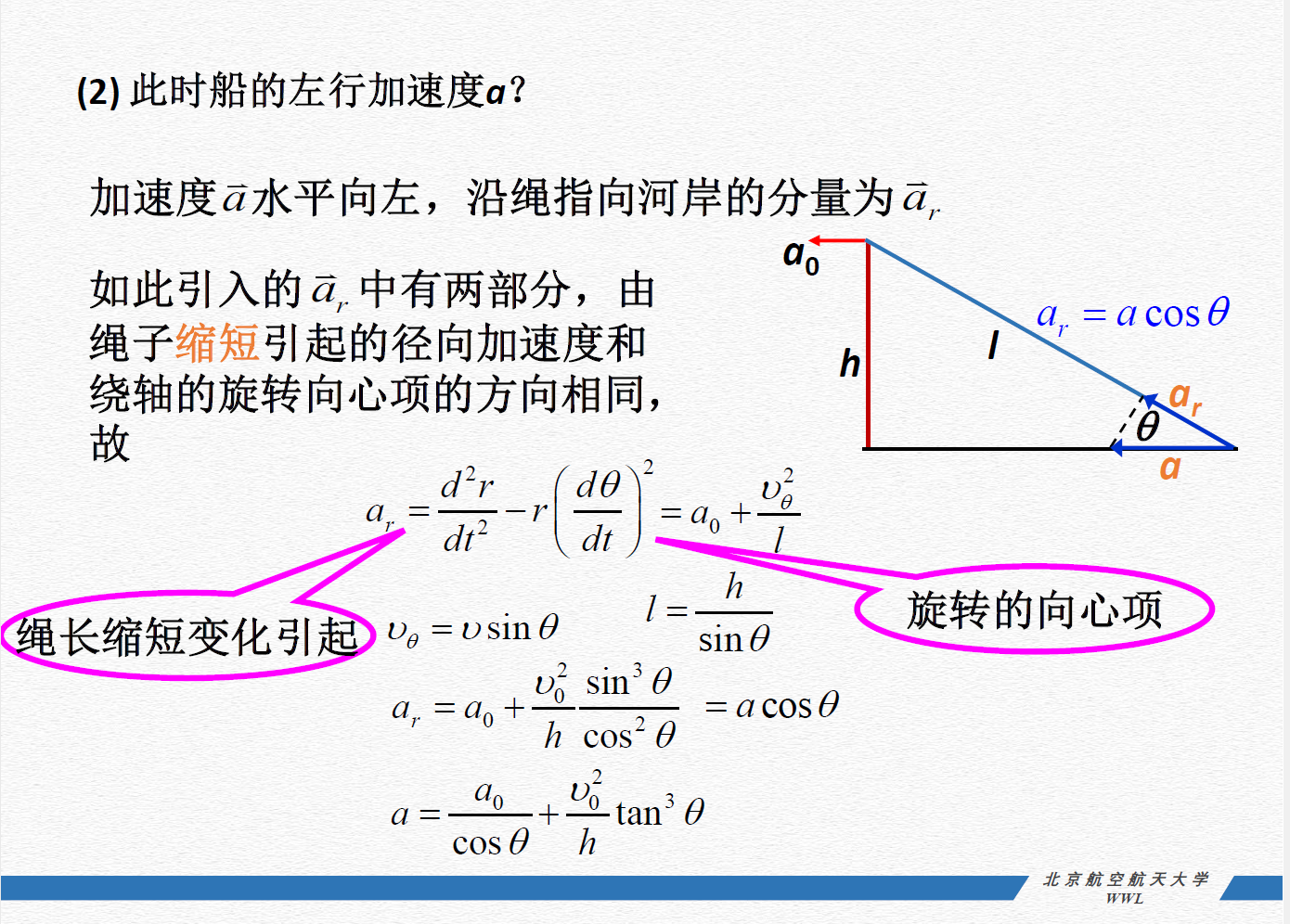
问题:如何理解"旋转的向心项"?
曲率半径计算公式¶
功能原理¶
注意: 这里应该是缓慢拉动, 分析非保守力做功对应机械能的变化.
惯性离心力势能¶
例 海平面方程
解析
回顾势能的定义: 对于保守力, 机械能是不变的,因此在保守场中, 只发生动能与势能的转化. 定义-A = \displaystyle -\int_0^x \vec{f}\cdot d\vec{r} = \phi_x - \phi_0, 因为我们知道当功为正时,系统的动能增加,当物体做负功时,动能就转化为"只与位置相关的储存起来的能量",显然,转化后的位置能量更大.当我们定义势能零点V_0 = \phi_0 = 0时, \Delta V= \phi_x = -A = -\Delta E_k, V_x = -A.
于是很显然可以定义**惯性离心力势能** E = -A = -\displaystyle \int\vec{f^*}\cdot d\vec{r} = -\int_0^r m\omega^2rdr = -{1\over 2}m\omega^2r^2
注意: 这个功A必须是从定义的势能零点积过来的!
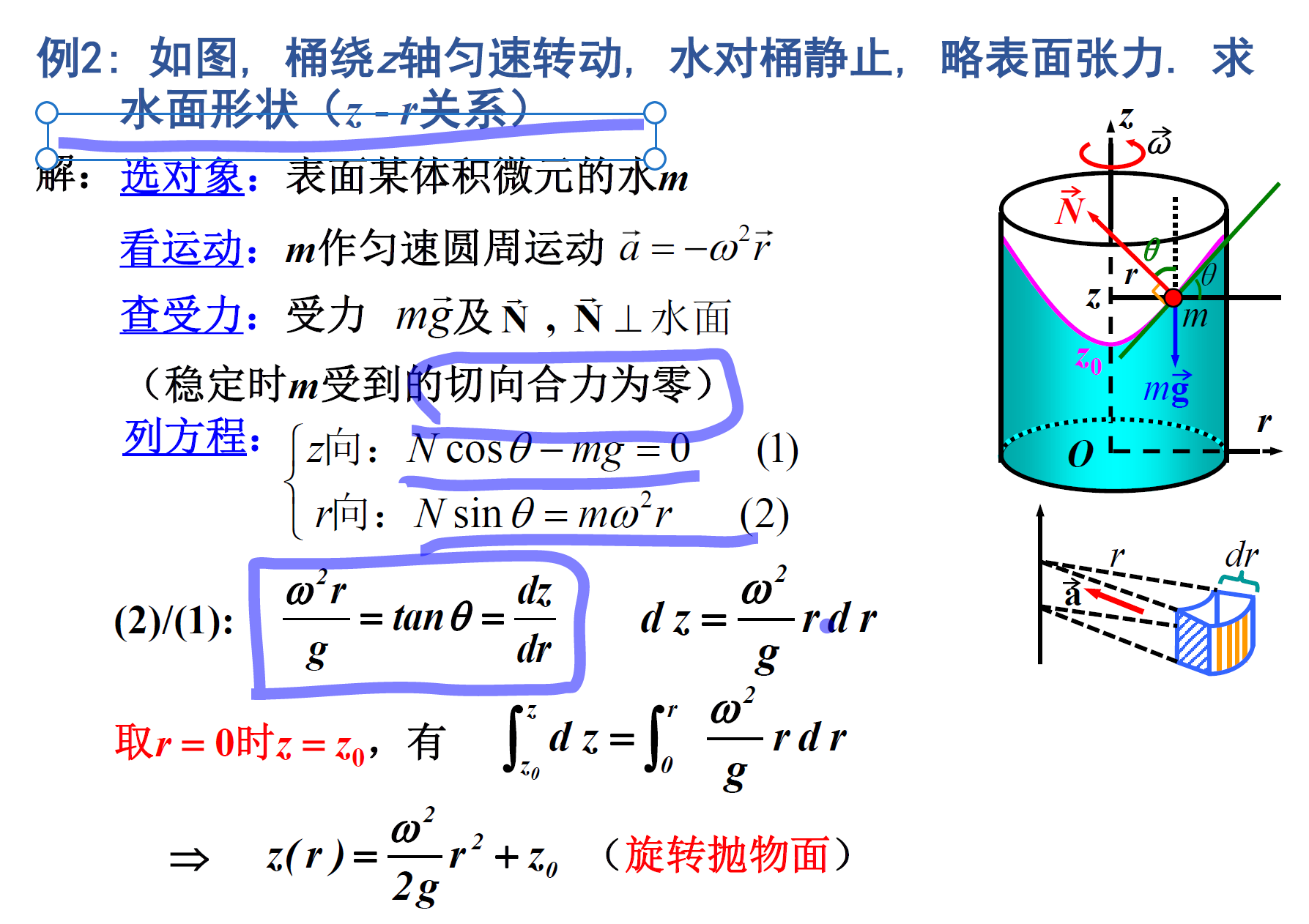
另解 (从惯性离心力势能角度)
考虑到水面是一个等势面,即**水面上的任一位置的重力势能和惯性离心力势能之和相等** $$ E = mgz - {1\over 2}m\omega2r2 = C\ \Rightarrow z = {\omega^2\over 2g}r^2 + z_0.\square $$
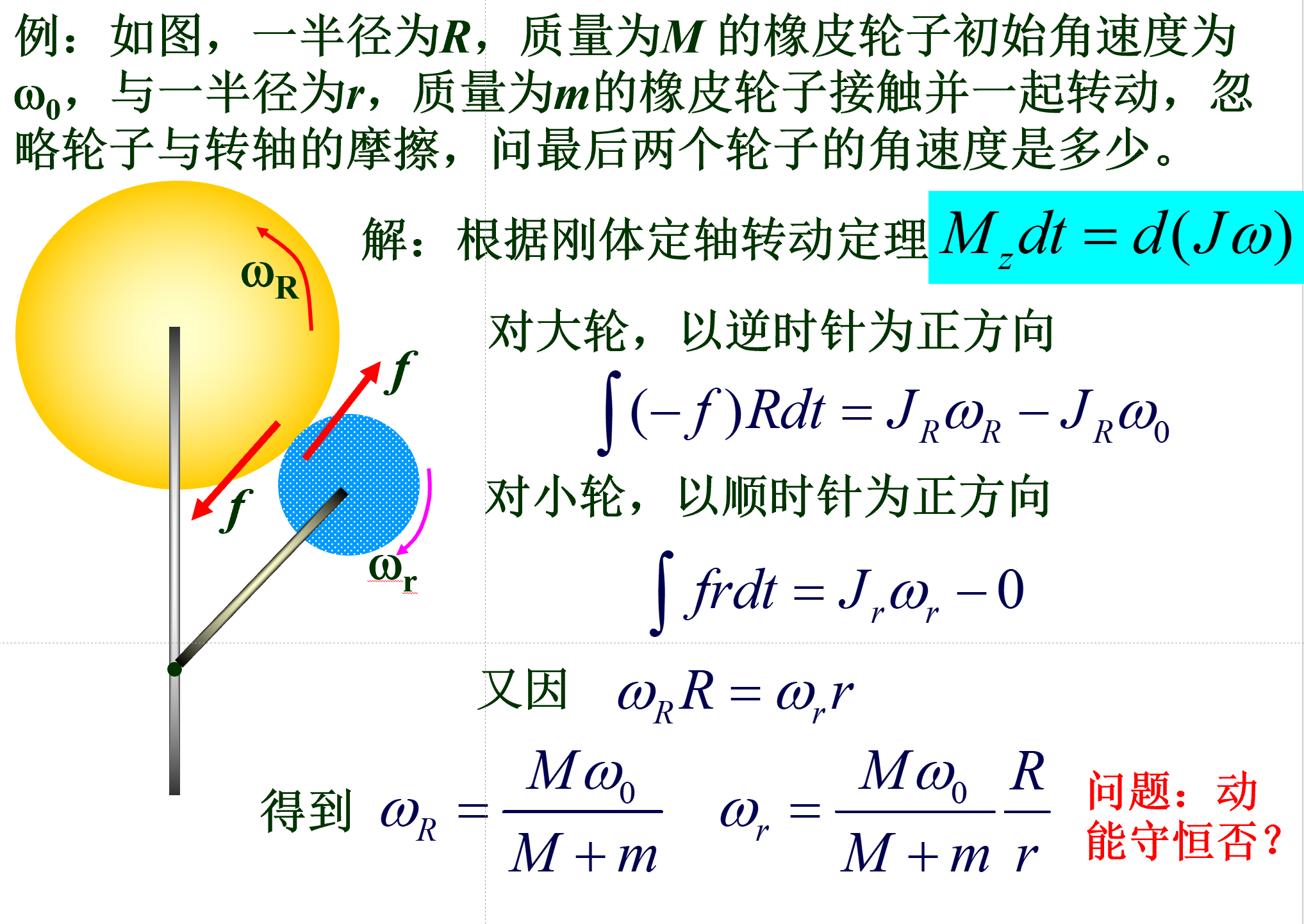
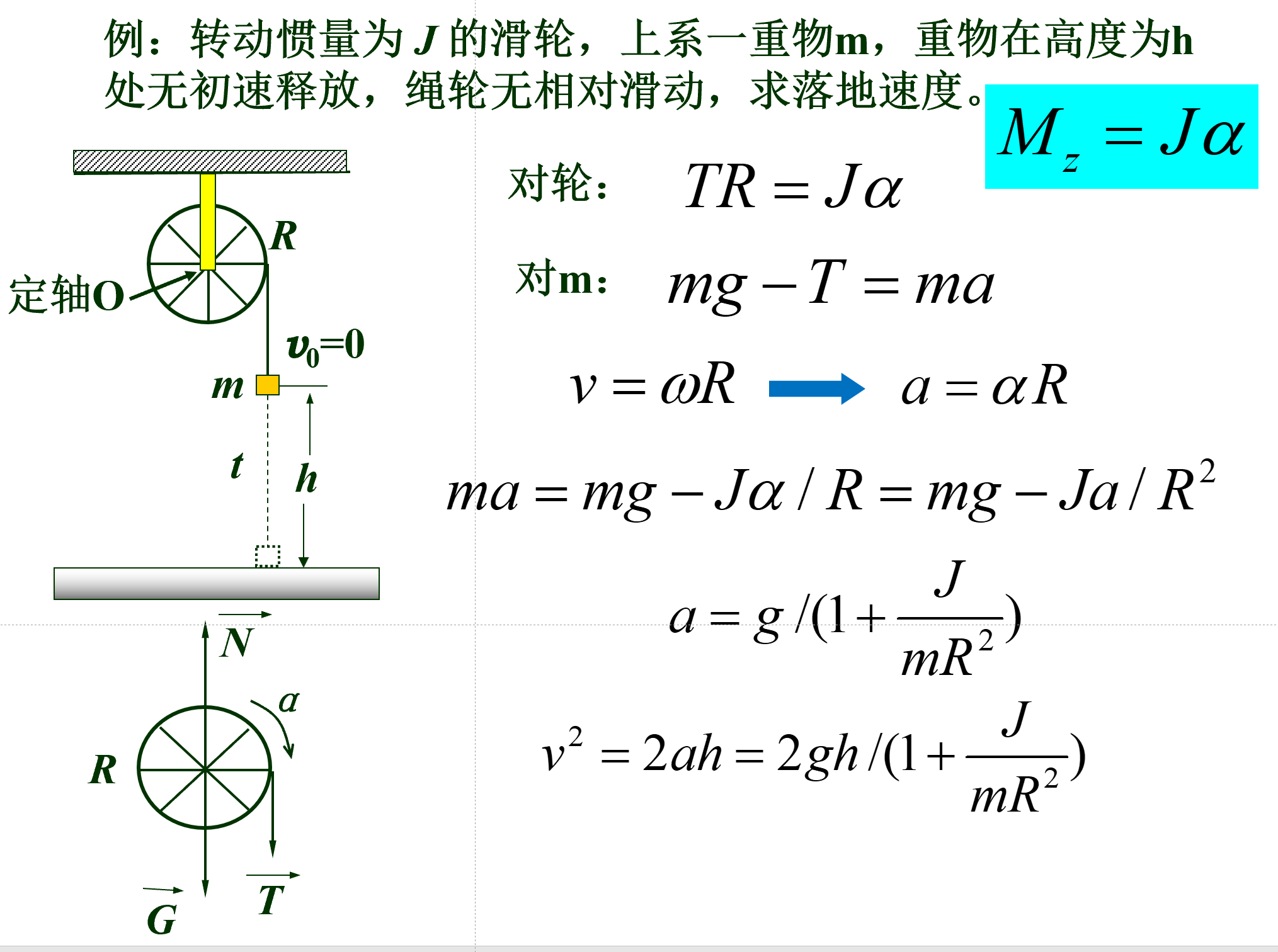
刚体¶
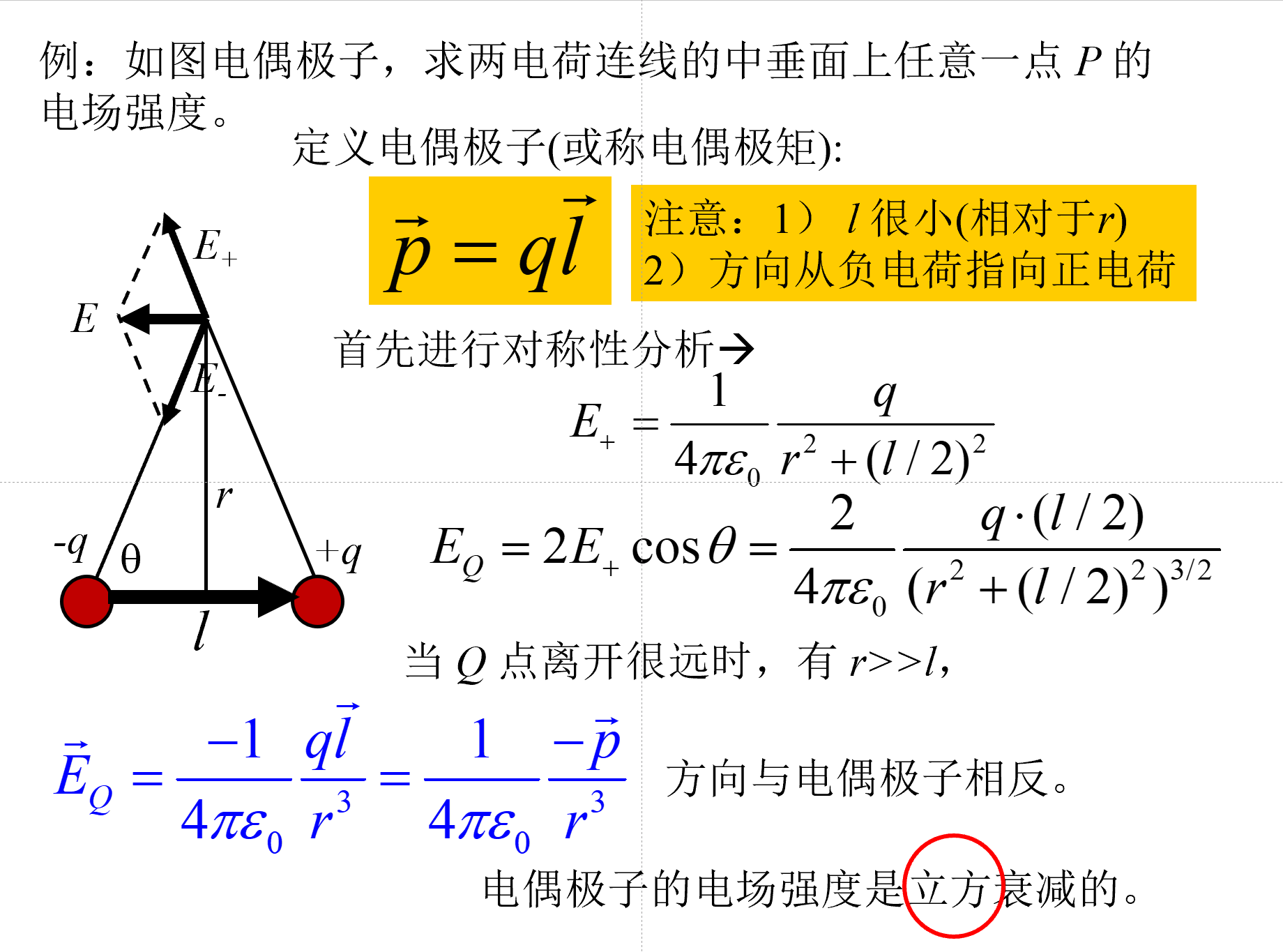
静电学¶
电偶极子¶
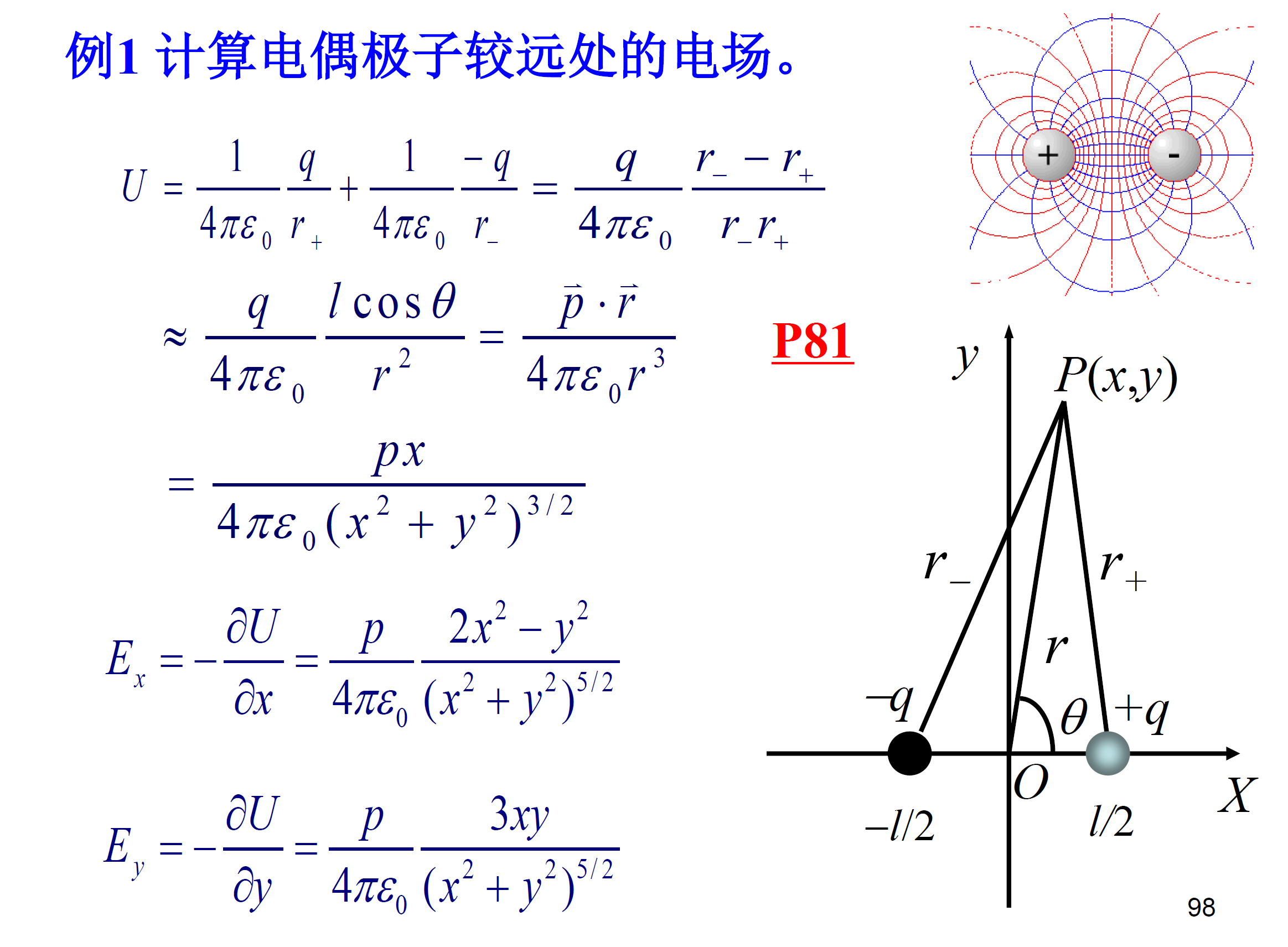
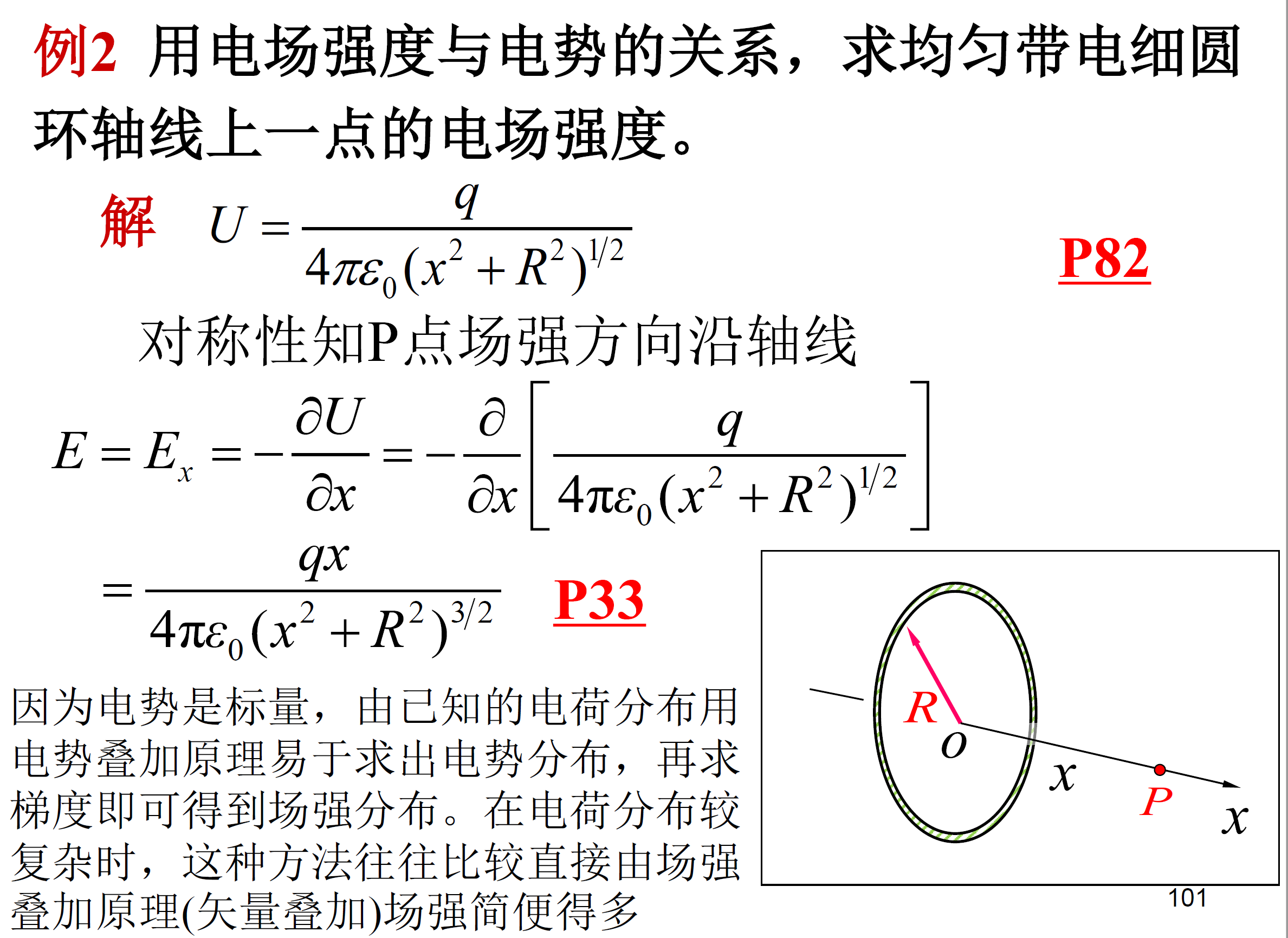
此题提供了一种求电场的方法: \displaystyle E_x = -{\partial U\over \partial x}
知识点¶
运动学¶
-
m{dv\over dt} = m{dv\over ds}\cdot v = \sum F_i
-
{1\over \rho} = \left|{y''\over [1 + (y')^2]^{3\over 2}}\right|\\ a_n = {v^2\over \rho} \Rightarrow\rho = {v^2\over a_n}
力学¶
-
dV = -dA\\ \Delta V = \int_{r_0}^{r_t} dV = -\int_{x_0}^{x_t} Fdx
-
dA = dE_k
-
\Delta E_k = A^{c} + A^{nc} = - \Delta V + A^{nc}\\ \Rightarrow A^{nc} = \Delta E_k + \Delta V = \Delta E_{m}
刚体¶
-
\begin{align} (1)& 总: J = \sum m_i r_i^2 = \int_V r^2dm\\ (2)& 圆环,转轴沿直径: J = 2\int_0^{\pi} \lambda Rd\theta \cdot (R\sin \theta )^2 =\lambda \pi R^3 = {1\over 2}m R^2\\ (3)& 薄圆盘,转轴通过中心,与圆盘垂直: J = m \int_0^R rdr = {1\over 2 } mR^2\\ (4)& 圆筒,转轴沿几何轴,内径r_1,外径r_2: J ={1\over 2 } \pi\rho(r_2^4 - r_1^4) = \pi \rho (r_2^2 - r_1^2)\cdot (r_1^2 + r_2^2) = {1\over 2}m(r_1^2+r_2^2)\\ (5)& 细棒,转轴通过中心,与几何轴垂直: J = {1 \over 12}m l^2.\\ & Pf. 设J = kml^2.利用转动惯量的线性性,将细棒拆成两小段.于是有,\\ & kml^2 = 2[k({m\over 2 })({l\over 2})^2 + ({m\over 2})({l\over 4})^2] \Rightarrow k = {1\over 12 }.(利用到了平行轴定理.)\\ (6)& 细棒,转轴过端点与棒垂直:J = {1\over 12} m l^2 + m ({l\over 2})^2 = {1\over 3}ml^2\\ (7)& 球壳,转轴沿直径: J = {2\over 3}mR^2\\ & Pf.I = \int r^2dm= \int (R\sin \theta )^2 \sigma2\pi R\sin \theta R\sin \theta = {1\over 2 }\int_0^{\pi\over 2}mR^2\sin^3\theta d\theta = {2\over 3}mR^2 \\ (8)& 球体,转轴沿直径: J = {2\over 5}mR^2\\ & Pf. I = \int dI = \int_0^R {2\over 3}r^2{4\pi^2r^2dr\over {4\over 3}\pi R^3}m = \int_0^R{2m\over R^3}r^4dr = {2\over 5}mR^2 \end{align}
-
垂直轴定理(仅用于薄平板) I = \sum m_i(x_i^2 + y_i^2) = I_x +I_y
-
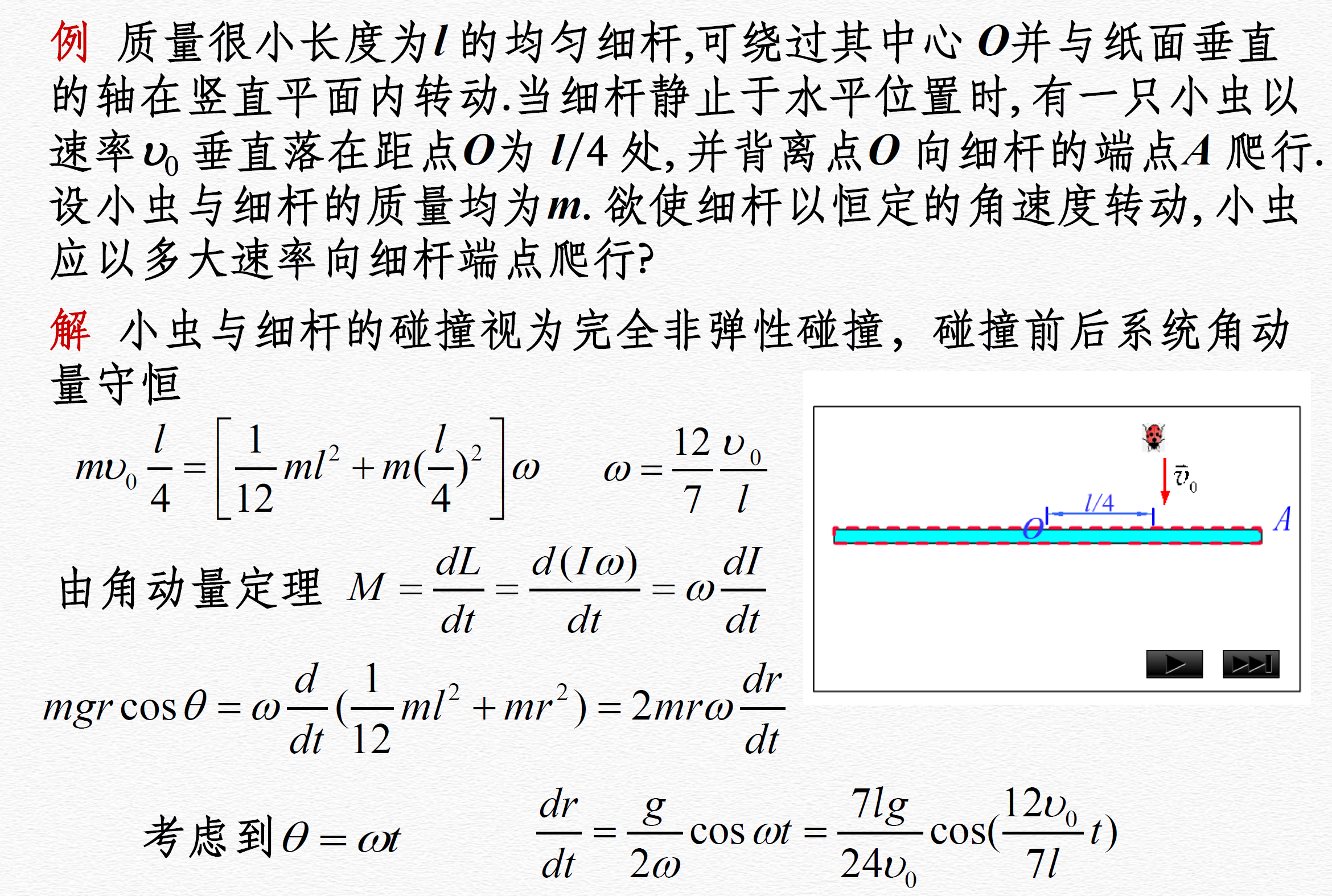
刚体抓住类比关系
- 刚体动力学问题的步骤
- 受力分析: \sum f_i = ma
- 角动量定理\sum M_i = J\beta
- 加速度和角加速度的运动学关系a = \beta r
- 计算得出加速度后 利用运动学公式求解速度等
冲量 动量¶
-
对于多数碰撞过程,有\tau \to 0, \int_0^{\tau} Gdt \approx 0.或者说是瞬间的冲击力F \gg G,因此可以忽略瞬间的重力的冲量.
-
碰撞问题
注意: 凡是碰撞问题 碰转过程一定会损失能量, 这个过程可以利用动量守恒/角动量守恒, 由碰撞前的速度求得碰撞后的速度, 此后的运动可以使用能量守恒!
变质量问题¶
绳子落地模型¶
火箭加速模型¶
静电学¶
几种典型电场
- 无限长直导线
- 无限大平板
-
-
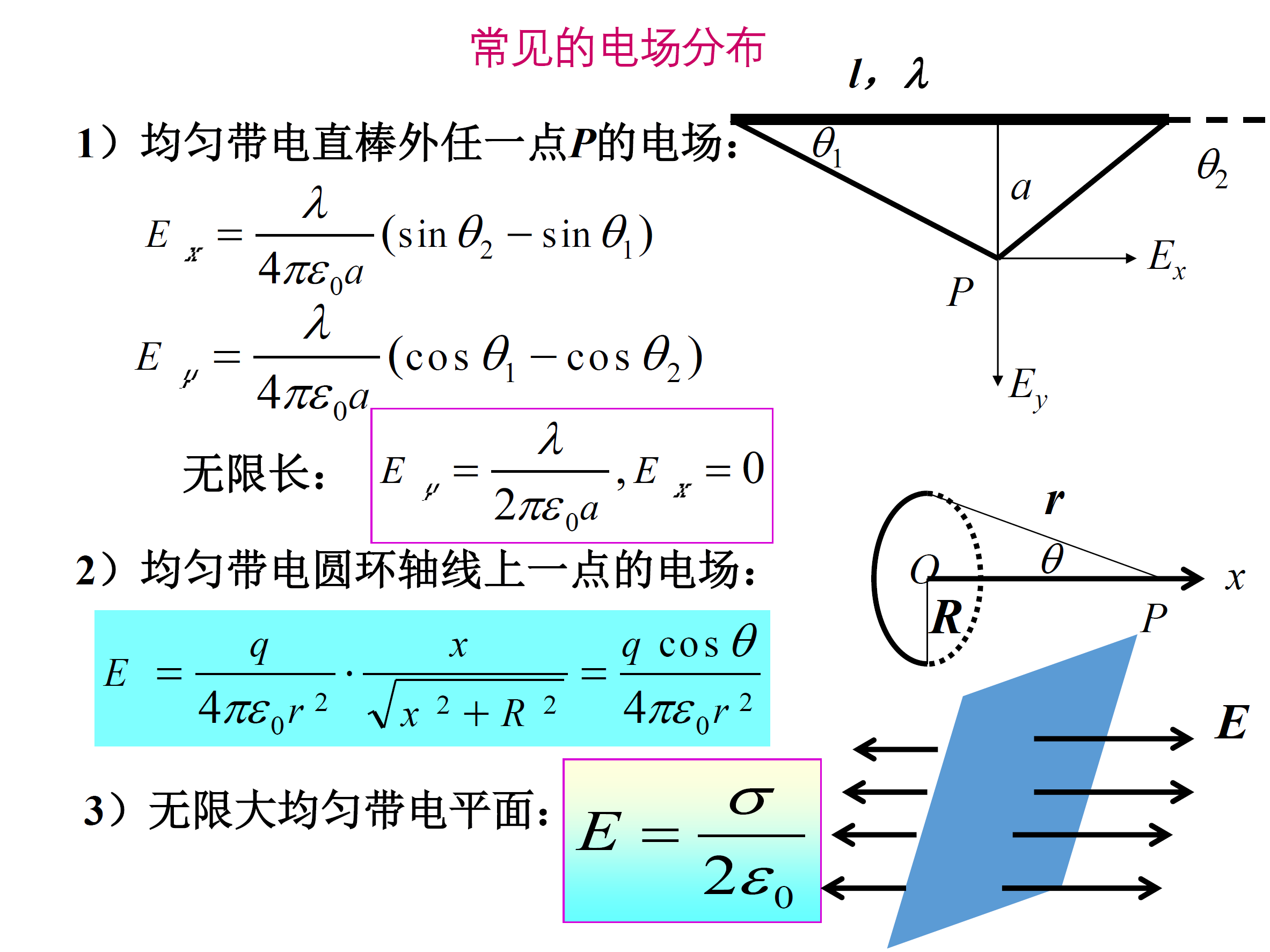
实心球体 $$ 设矢径为\vec{r}, \ \oiint_S \vec{E}\cdot d\vec{S} = \vec{E} \cdot 4\pi r^2= {\rho {4\over 3}\pi r^3\over \varepsilon_0}\hat{r}\ \Rightarrow \vec{E} = {\rho\over 3\varepsilon_0}\vec{r} $$
电场能量¶
-
E = \sum {1\over 2}q_iV_i\\ V_i为除该点自身产生的电势之外的电势,如果考虑自身电势的话,就没有意义了.
-
平板电容器的静电能 E = {1\over 2}{Q^2\over C} = {1\over 2}CU^2
-
电场密度$E = \displaystyle \iiint_V \omega dV = \iiint {1\over 2}\varepsilon E^2dV $
电流¶
-
dI = {dV\over R} = {dV\over \rho dl/ds} = {dVds\over\rho dl} = \sigma{dVds\over dl}\\ \Rightarrow {dI\over ds}= \sigma {dV\over dl}\\ \Rightarrow \vec{j} = \sigma\vec{E}.
这个公式说明了这其实是欧姆定律的微观形式.
- 等效环形电流dI = \displaystyle {dq\over T}.
电容¶
-
几种常见的电容
-
平行板电容 C = {Q\over U} = {\sigma S \over{\sigma\over \varepsilon_0} } = \varepsilon_0 S
-
球形电容 $$ E(x) = {q\over \varepsilon_0 4\pi x^2}\ U_{ab} = \int_{R_a}^{R_b} {q\over \varepsilon_0 4\pi x^2} dx = {q\over 4\pi \varepsilon_0} {R_b- R_a\over R_a R_b}.\ C = {Q\over U} = 4\pi \varepsilon_0 {R_aR_b\over R_b - R_a}. $$
-
球形孤立电容 $$ E(x) = {q\over \varepsilon_0 4\pi x^2}\ U = \int_{R}^\infty {q\over \varepsilon_0 4\pi x^2} dx = {q\over 4\pi \varepsilon_0} {1\over R}.\ C = {Q\over U} = 4\pi \varepsilon_0 {R}. $$
静磁学¶
-
几种常见磁感应强度
-
-
-
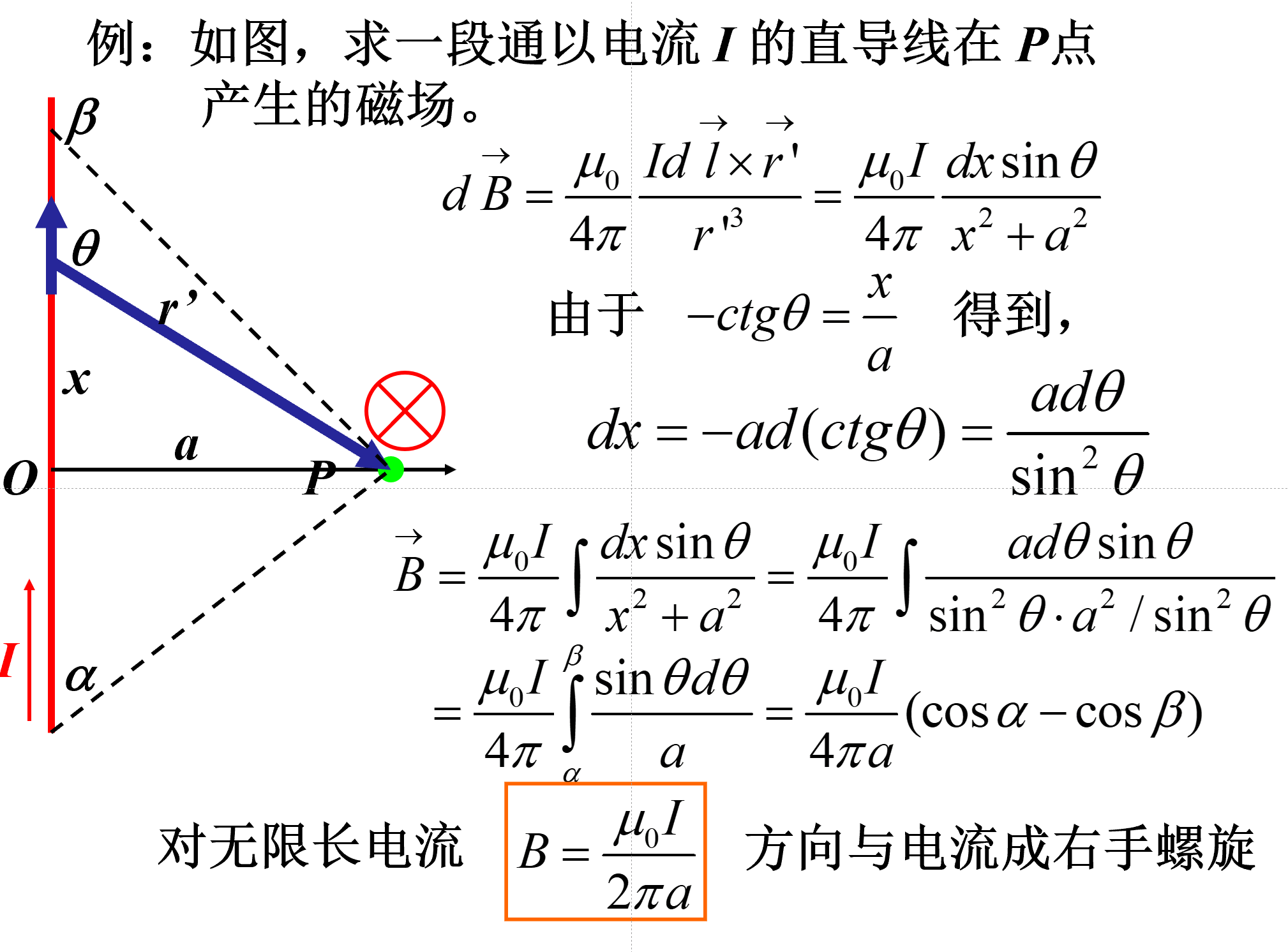
通电螺线管
- 螺绕环 $$ \oint B\cdot dl = B2\pi r = NI\ B = {N\over 2\pi r}I \approx nI(l \gg 环的截面半径)\ $$
热学¶
-
基本公式 $$ \begin{align} (1)& pV = \nu RT\ (2)& p = {2\over 3}n\bar{\varepsilon_k},式中\bar{\varepsilon_k}为平均平动动能,n为单位体积内的分子数 \ (3)& \bar{\varepsilon_k} = {3\over 2}kT\ (4)& E = \nu {i\over 2}RT\ (5)& {dN\over N} = f(v)dv \Rightarrow {\Delta N\over N} = f(v)\Delta v, \int_0^{\infty} f(v)dv = 1\ (6)& f(v) = 4\pi ({m_0\over 2\pi kT})^{3\over 2}e^{-{m_0 v^2\over 2kT} }v^2\ (7)& \bar{v} = \int vf(v)dv = \sqrt{8kT\over \pi m} = \sqrt{8RT\over \pi M} \approx 1.60\sqrt{RT\over M}\ (8)& v_{rms} = \sqrt{\bar{v^2}} = \sqrt{3kT\over m} = \sqrt{3RT\over M} \approx 1.73\sqrt{RT\over M}\ (9)& {df\over dv} = 0\Rightarrow v_p = \sqrt{2kT\over m} = \sqrt{2RT\over M} \approx 1.41\sqrt{RT\over M}\ (10)& \bar{\lambda} ={1\over \sqrt{2} \pi d^2n} = {kT\over \sqrt{2} \pi d^2 p}\ (11)& \overline{Z} = \sqrt{2}\pi d^2 n \bar{v}\ \end{align} $$
-
热力学四定律
-
第零定律: 如果两个物体与都处于确定状态的第三物体处于热平衡, 则该两个物体彼此处于热平衡.
- 第一定律: 外界对系统传递的热量, 一部分是使系统的内能增加, 另一部分是用于系统对外做功.
-
第二定律:
- 开尔文表述: 不可能制成一种循环动作的热机, 只从一个热源吸收热量, 使之全部变为有用的功,而不产生其他影响
- 克劳修斯表述: 热量不可能自动地从低温物体传向高温物体.
-
dA = pdV,dV为正表明气体对外作正功. dQ = dE + dA = dE + pdV
-
准静态过程 $$ \begin{align} (1)& 等体: dA = 0, C_{V,m} = {i\over 2} R, \ (2)& 等压: C_{p,m} = {i+2\over 2}, \gamma = {i+2\over i} > 1\ (3)& 等稳: dE = 0, Q = A = \nu RT\ln {p_1\over p_2}\ (4)& 绝热: dQ = 0, dA = pdV = - dE pV^{\gamma} = C.\ \end{align} $$
-
卡诺定理:
-
在同样的高低温热源之间工作的一切可逆机, 不论用什么工作物, 效率都等于(1 - {T_2\over T_1}).
- 工作于两个确定温度之间的热机中， 可逆热机的效率最高。
$$ \eta_{热机} = {A\over Q_{吸}} = {Q_{吸} - Q_{放}\over Q_{吸}} = 1 - {T_{低}\over T_{高}}\ \eta_{制冷机} = {Q_{吸}\over A} = {T_{低}\over T_{高} - T_{低}} $$
熵¶
### 数学基础
-
立体角
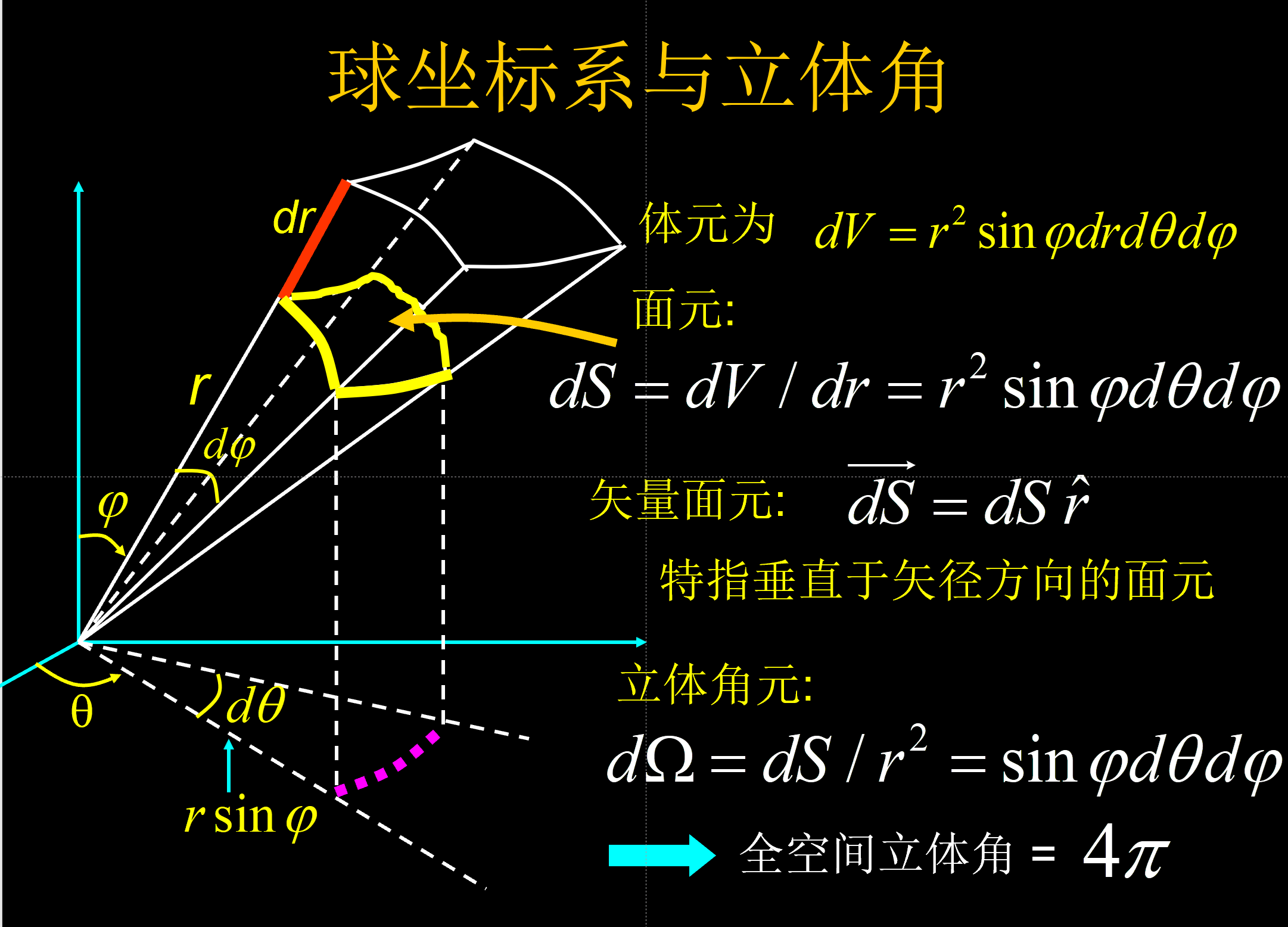
注意点¶
- 力学题做题步骤:
- 选对象
- 看运动
- 分析力
- 列方程
- 验结果/量纲
- 过渡到特殊值(消去微分方程解常数C,得到特解)
-
变化趋势: 思考这个结论是否符合直观(合理)
-
写完记得检查量纲!
- 注意$\displaystyle U_{ab} = U_a - U_b =-\int_b^a \vec{E}\cdot d\vec{r} = \int_a^b \vec{E}\cdot d\vec{l} $ 因为\displaystyle \Delta V = V_t - V_0 = -A = - \int_{r_0}^{r_t} \vec{f}\cdot d\vec{r} 因为E_x = \displaystyle -{\partial U\over \partial x} .
- 电容器注意是连接电动势的状态,则U不变,否则Q不变.
- 势能总是要先说明**势能零点**!
- 角动量守恒不要忘了滑轮自身的角动量!
- 高斯定理取高斯面后计算电通量时注意==穿出为正,穿进为负==!
问题¶
- 接地问题? 接地等价于什么?
- 薄球壳也要视作内表面和外表面?
- 什么时候切断接地导线有/无影响?
刷题记录¶
chap 5¶
- 5-11 求速率大小在v_p\sim 1.01v_p之间的气体分子占总分子数的百分率.
利用f(v)\Delta v = {\Delta N\over N}.本题中取为f(v_p) 利用v_p改写麦克斯韦速率分布律, $$ v_p = \sqrt{2RT\over M},用v_p改写麦克斯韦速率分布,\ {\Delta N\over N} = f(v)\Delta v = 4\pi ({m_0\over 2\pi kT})^{3\over 2}e^{-{m_0 v^2\over 2kT} }v^2\Delta v= {4\over \sqrt{\pi}}({v\over v_p})^2 e^{-({v\over v_p})^2}({\Delta v\over v_p})\ 令W = {v\over v_p} ,\Delta W = {\Delta v\over v_p},\ f(v)\Delta v = {4\over \sqrt{\pi}} W^2 e{-W2}\Delta W\ 带入W = 1, \Delta W = 0.01,\ {\Delta N\over N} = 0.83\%. $$
chap 7¶
RC回路充电放电 p300¶
-
充电过程 $$ \mathscr{E} = U_R +U_C = {dq\over dt}R + {q\over C}\ \Rightarrow R{dq\over \mathscr{E} - {q\over C}} = dt\ \Rightarrow -CR\ln(\mathscr{E} - {q\over C}) = t + C^*\ 带入初值条件 t= 0, q=0.\ q = C\mathscr{E}(1 - e^{-{t\over RC}}). $$
-
放电过程 $$ 0 = R{dq\over dt} + {q\over C}\ \Rightarrow q = q_0e^{-{t\over RC}}. $$
电容器的充放电过程快慢取决于乘积\tau = RC,它具有时间的量纲,叫做RC电路的==时间常数==或==犹豫时间==.在经过3\tau \sim 5\tau后, 充放电基本已经结束.
地球与大气层构成RC回路 p318¶
习题¶
-
7-11 电场叠加原理
-
7-12 电场叠加原理 难度在于积分方式
均匀带电半球面球心处场强的多种求解方法 - 道客巴巴 (doc88.com)
最自然的方法是建立极坐标系积分
也可以套用圆环的电场结论
还可以直接利用E = -\nabla V 问题是: 为什么E = -{\partial V\over \partial R}?
-
7-18 Gauss公式
-
7-34 平行板电容器的电场公式运用
-
7-35 内外球壳 考察对接地的理解
-
7-39 电容器 接地
-
7-46 电容器 插入新板
-
7-49 ==电介质==电容器(不讲武德)
-
7-51 简单RC放电过程 电容器能量
-
7-55 电位移 电容器 电介质
-
7-60 好题! 大球套小球 一题多解
Sol\ 1 .分析电荷分布,得到电场分布,对全空间用能量密度积分.
Sol\ 2.看做是双球电容+孤立电容的串联
- 7-61 电容器能量
chap 8¶
-
8-8 磁通量计算\phi = \vec{B}\cdot \vec{S} = BS\cos \alpha
-
8-9 磁感应强度的矢量叠加
-
8-10 运用有限长指导线的磁场公式B =\displaystyle {\mu_0I\over 2\pi}(\cos\alpha - \cos \beta).
-
8-11 同上
-
8-12 半无限长直导线 + 部分圆形导线叠加
-
8-13 简单电路 磁感应强度的叠加
-
8-17 稍微考察建模分析能力 无限长直导线的有向叠加
-
8-18 比较经典的旋转体等效环路电流
解析 在圆盘上取半径为r宽为dr的细圆环，环上的电量为dq = \sigma 2\pi rdr = {2q\over R^2}rdr.
根据电流的定义dI = {dq\over dt},dq就是在圆盘绕轴转动的一个周期内，通过盘的径向宽为dr线段的电荷量。所以，有dI = \displaystyle {dq\over T}（其实很好理解，在一个周期T内，这个环带上的所有电荷都经过了一次*这条线*，利用平均的思想即可） $$ dI = {dq\over T} = \omega{dq\over 2\pi} = {q\omega\over \pi R^2}rdr\ dB = {\mu_0q\omega \over 2\pi R^2}dr. $$ 然后对r积分即可。
-
8-21 等效环形电流 注意不要漏！
-
8-22 无限长直导线磁感应强度 磁通量\Phi =\displaystyle \int\vec{B} \cdot d\vec{S}
-
8-24 安培环路简单应用
-
8-36 安培力的矢量积分
-
8-48 螺绕环 相对磁导率 磁化电场-
-
8-50 磁介质