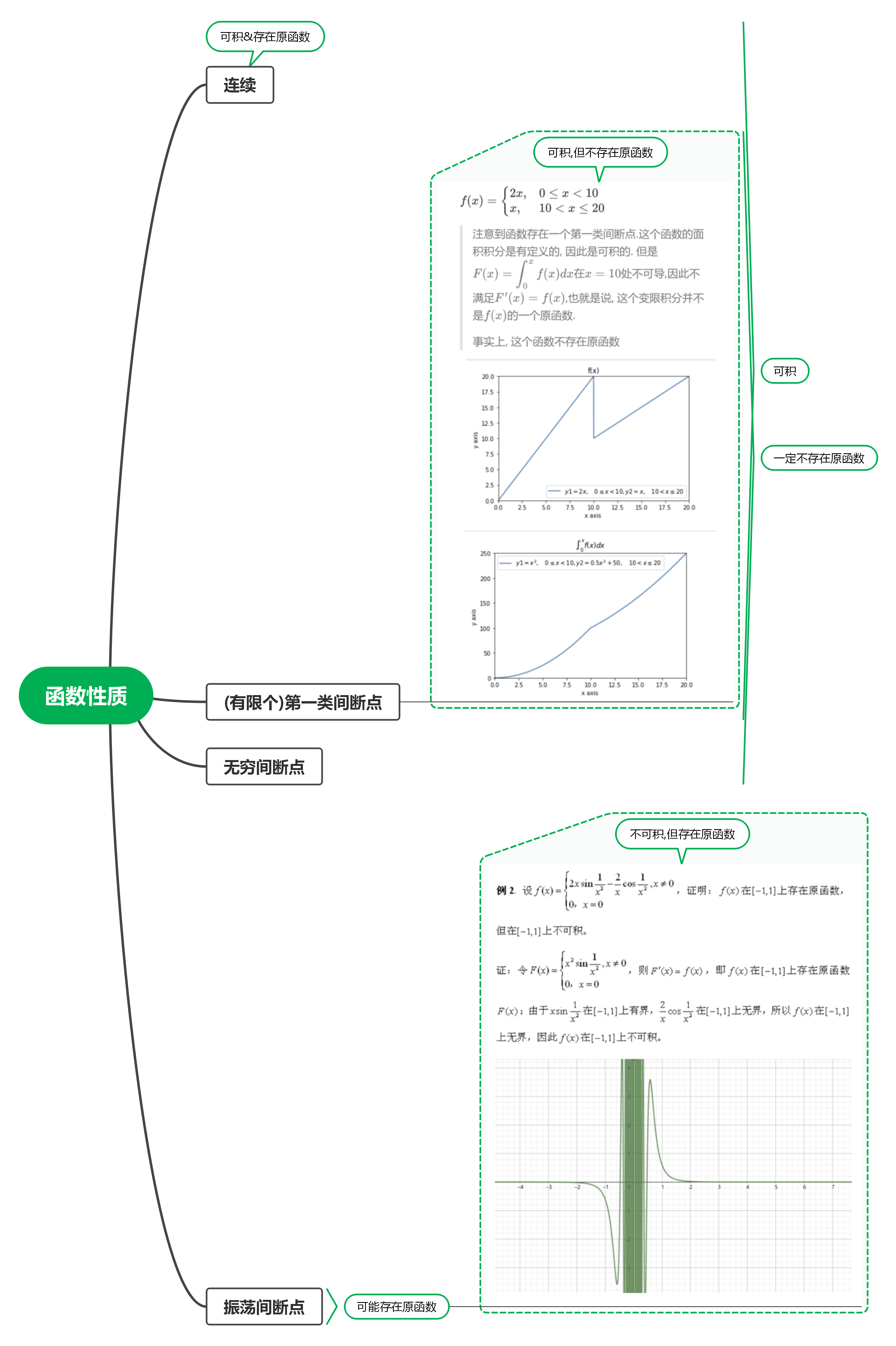
可积一定有原函数吗?

看到一个问题: 可积函数一定有原函数吗? 没想到竟然把我给问住了(可见本人的数学学的还是不扎实),上知乎一阵搜索,看的云里雾里,总算看明白了一点皮毛,于是就稍微整理一下吧.

由于作者水平有限,本文错漏缺点在所难免,希望读者批评指正.

首先, 我们来回顾几个基本的定义.

  • 可积:

注意:本文中的可积是指**黎曼可积** 针对的函数积分不包括**反常积分**.

如果f(x)在[a,b]上定积分存在,我们就说f(x)在[a,b]上可积

充分条件 若函数在闭区间内连续或存在有限个第一类间断点(左右极限存在)

我们可以认为, 函数在某个区间可积, 就是可以画出函数在这个区间围成的面积存在.

  • 变限积分: $$ \int_a^x f(t)dt = f(x)在[a, x]上围成的面积. $$

  • 原函数: $$ \exists F(x), \forall x_0 \in [a, b], F'(x) = f(x) $$

  • 原函数存在定理:若f(x)在[a,b]上连续,则必存在原函数。(充分条件)

  • 如果f(x)不连续，有第一类可去、跳跃间断点或第二类无穷间断点，那么包含此间断点的区间内，一定不存在原函数；
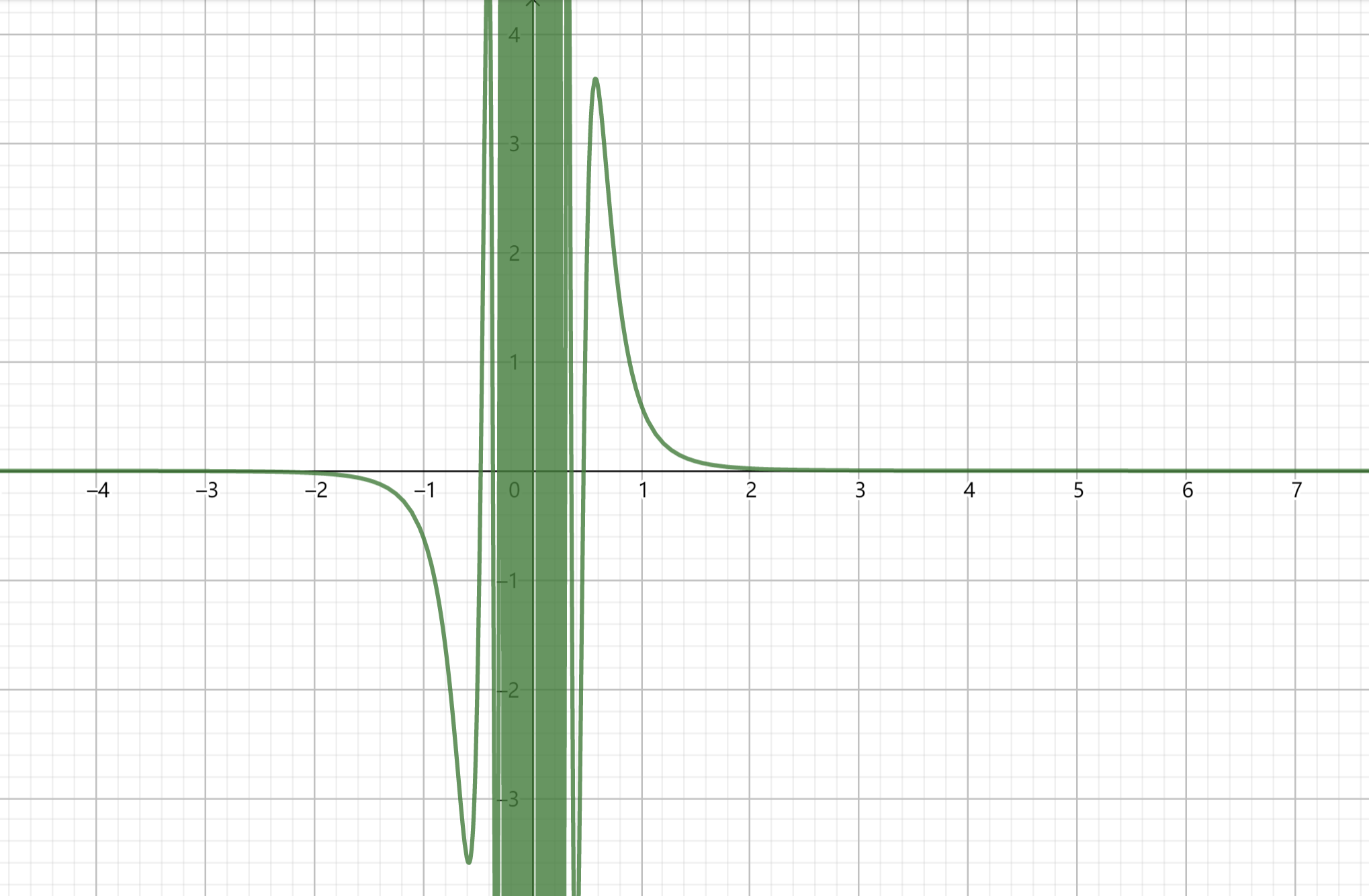
  • 如果f(x)不连续，有第二类振荡间断点，那么包含此间断点的区间内，原函数可能存在，也可能不存在。

例

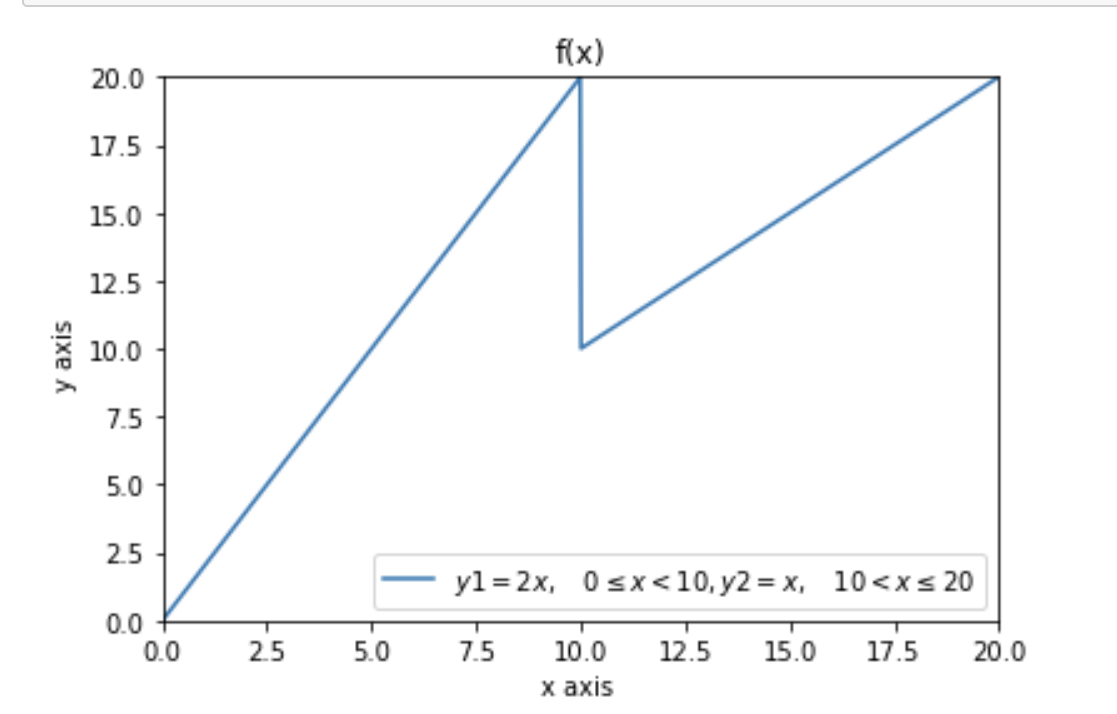
f(x) = \begin{cases} 2x, & 0 \le x < 10 \\ x, & 10 < x \le 20 \end{cases}

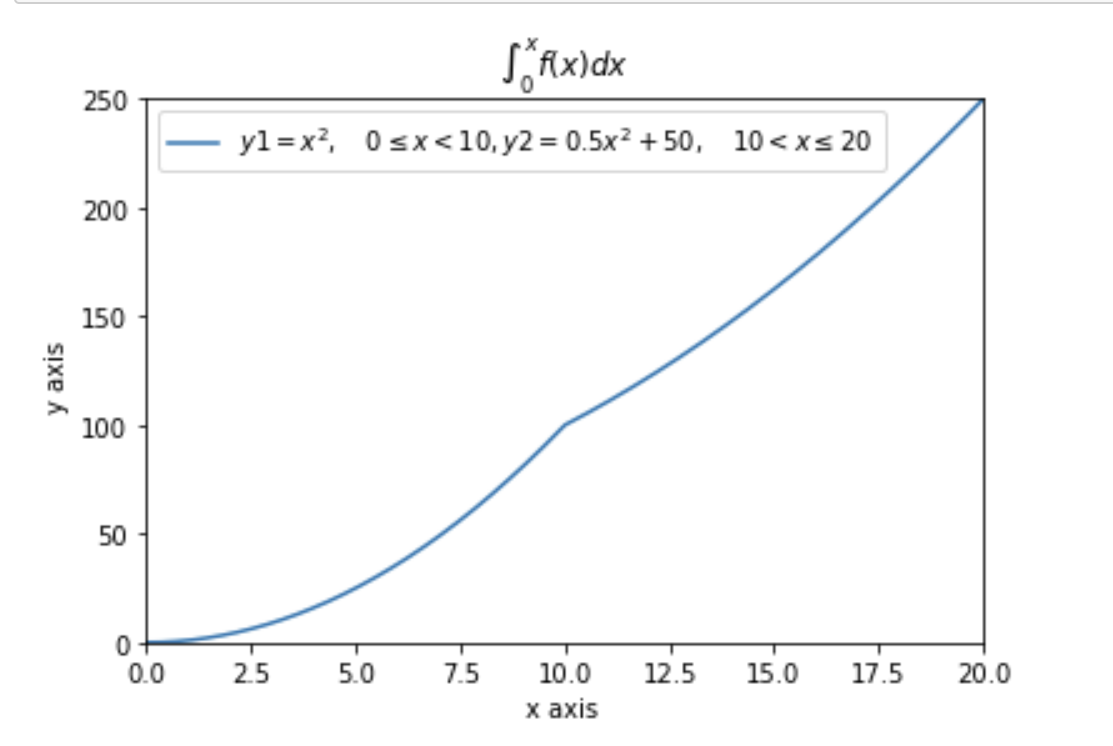
注意到函数存在一个第一类间断点.这个函数的面积积分是有定义的, 因此是可积的. 但是F(x) = \displaystyle \int_0^x f(x)dx在x = 10处不可导,因此不满足F'(x) = f(x),也就是说, 这个变限积分并不是f(x)的一个原函数.

事实上, 这个函数不存在原函数

image-20220710143117696

image-20220710143847031

img

image-20220710153459431

因此, 我们可以有一个初步的结论:

conclusion