数字逻辑与计算机组成¶

数字逻辑与计算机组成

第一章二进制编码¶

第一讲计算机系统概述¶

冯诺依曼结构计算机
- 最重要的思想: "存储程序"(stored memory)的工作方式
- 存储单元
- 运算单元
- 控制单元
- I/O
现代计算机结构模型
- CPU: 中央处理器
- PC: 程序计数器
- MAR: 存储器地址寄存器
- ALU: 算术逻辑部件
- IR: 指令寄存器
- MDR: 存储器数据寄存器
- GPRs: 通用寄存器组

计算机是如何工作的?¶

一个比喻

做菜前: 原材料[数据]和菜谱[指令]都按序放在冰箱桌柜[存储器]里, 每个存放位置都给一个编号[存储单元地址]. 每个盘跌也有编号[GPRs的具体寄存器指定].
菜谱上信息: 原料的存放位置, 做法, 做好的菜放在哪里等首先, 我告诉爸妈: 从存放在5号位置的菜谱开始顺着做
开始做菜:
- 第一步: 去菜谱
- 第二步: 看菜谱
- 第三步: 取原材料
- 第四步: 洗, 切, 炒
- 第五步: 送菜
- 第六步: 看下一个菜谱

计算机的语言¶

高级语言->汇编语言->机器语言

机器级语言---面向机器的语言¶

Note

机器语言和汇编语言都属于机器级语言, 且一一对应

高级语言¶

与具体的机器结构无关
面向算法描述, 比机器语言描述能力强得多
高级语言中一条语句对应几条, 几十条, 甚至几百条指令
处理逻辑分为三种结构: 顺序结构, 选择结构, 循环结构
有两种转换方式: 编译/解释

编译vs.翻译

编译: 编译（Compile）的过程是把整个源程序代码翻译成另外一种代码，翻译后的代码等待被执行或者被优化等等，发生在运行之前，产物是 另一份代码 。
翻译: 解释（Interpret）的过程是把源程序代码一行一行的读懂，然后一行一行的执行，发生在运行时，产物是 运行结果 。

图片示例

注: c++~编译器, python~解释器

开发和运行程序¶

早期的程序开发: 直接输入指令和数据, 启动后把第一条指令地址传送PC开始执行
现代程序开发:
需要编辑器编写源程序
需要一套翻译转换软件处理各类源程序
- 编译方式: 预处理程序->编译器->汇编器->链接器
- 解释方式: 解释程序
需要一个可疑执行程序的界面:
- GUI: 图形用户界面
- CUI: 命令行用户界面
  还需要配合操作系统, 语言处理系统(语言的运行时系统,操作系统内核,指令集体系结构,计算机硬件)
  - 支撑程序开发和运行的环境由系统软件提供
  - 最重要的系统软件是操作系统和语言处理系统
  - 语言处理系统运行在操作系统之上, 操作系统利用指令管理硬件

现代计算机系统的层次¶

应用程序->语言处理系统->操作系统->指令集体系结构->计算机硬件

语言处理系统

包括: 各种语言处理程序性(如编译, 汇编, 链接), 运行时系统(如库函数, 调试, 优化等功能)

本课程主要内容¶

二进制编码
数字逻辑电路
运算功能部件
指令集体系结构
中央处理器

第二讲二进制编码¶

回顾: 计算机是如何工作的?

"存储程序"工作方式: 程序(指令) 数据执行

计算机只能理解执行机器指令, 只能存储二进制数据.

ISA(指令集体系结构)规定了如何使用硬件:

可执行的指令的集合
指令可以接受的操作数类型
操作数能存放到哪些地方: 寄存器, MM
指令执行过程的控制方式, 包括程序计数器.

总结就是: ISA规定了指令有哪些, 怎么用.

真值 vs. 机器数

机器数是计算机内部的0/1序列

真值是机器数在真实世界中的表示

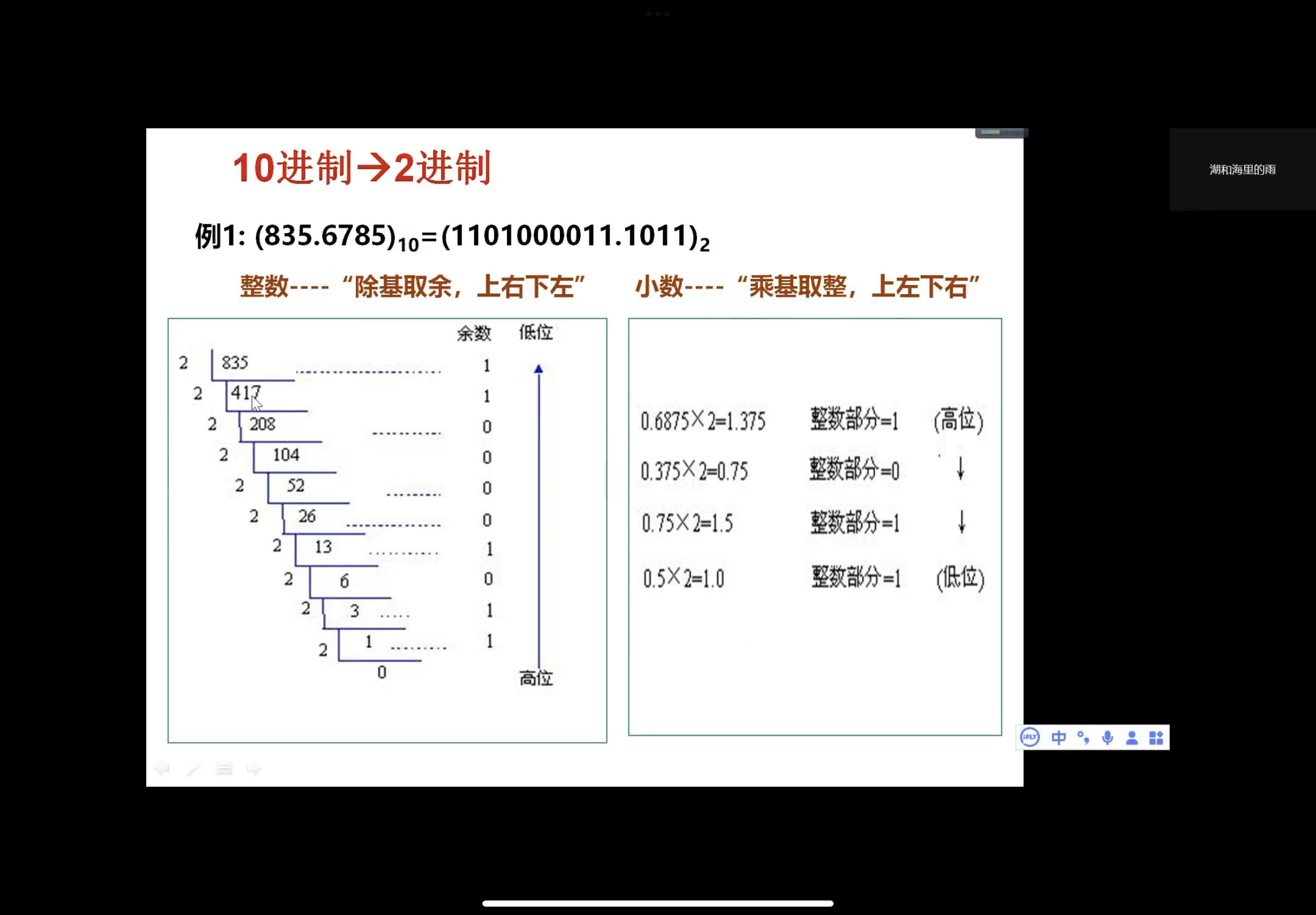
进制转换¶

1. 二进制八进制十六进制互转¶

Oct/ Hex -> Binary

直接转换

Binary ->Oct/ Hex

整数部分, 从低位开始, 每¾位一组, 缺位补0

小数部分, 从高位开始, 每¾位一组, 缺位补0

2. 二进制与十进制互转¶

Binary -> Decimal

例: 1101.101B

$\begin{aligned} &1 \times 2^3 + 1 \times 2^2 + 1 \times 2^0 + 1\times 2^{-1} + 1\times 2^{-3}\\ &= 8 > + 4 + 1 + 0.5 + 0.125\\ &= 13.625 \end{aligned}$

Decimal -> Binary

3. 八进制十六进制与十六进制¶

十进制->二进制->八进制/十六进制

技巧

配凑法: 记住基本的2的倍数对应的十进制表示, 加加减减配成好转换的数.

数值数据的表示¶

数值数据的三要素:
进位计数制
定/浮点表示
如何用二进制编码

因此, 对于如01011001这样的数, 不能简单认为是二进制定点数的原码形式, 需要给出"三要素".

补码的表示¶

运算器是一个模运算系统

假定补码有n位, 则: $[X]_c = 2^n + X$ ,

表示范围: $-2^{n-1} < [X]_c < 2^{n-1} - 1$

Question

什么时候"overflow"会导致最终结果正确/错误?

浮点数表示¶

IEEE 754 浮点数标准¶

Normalized numbers（规格化数）

32位浮点数

Sign 0
Mantissa 尾数 9-31(规格化规定0.1xxx, 因此小数点后总是1, 不需要表示, 因此可以表示31 - 9 + 1 + 1 = 24位尾数)
Radix(base)
Exponent阶码 1-8(偏置常数127)

64双精度浮点数

sign 0
Mantissa 尾数 12-63(63 - 12 + 1 + 1 = 53)
Radix
Exponent阶码 1-11(偏置常数1023)

数据的宽度和存储¶

存储¶

编址单位: 对主存单元编号时, 具有相同编号的二进制数, 其主存单元的编号称为地址. 通常的编址单位为8, 即字节.
字地址: 按字节编址时, 一个字可能占用几个存储单元, 字地址就是这几个连续存储单元地址中的最小值.
大端: 数据字的LSB放在大地址单元中.
小端: 数据字的LSB放在小地址单元中.

Summary

冯诺依曼结构
计算机的功能: 执行指令对数据进行处理
二进制(补码/IEEE754)

第二章¶

第一讲逻辑门和数字抽象¶

逻辑门(Logic gate)¶

具有 允许或禁止 信号传输门电路

Input: 1⁺
Output: 1 表明输入信号间的逻辑关系
图形符号
逻辑变量(符号): 输入信号输出信号 (0/1)
逻辑表达式: 用逻辑运算符来链接逻辑变量
真值表
最基本运算(基本逻辑门): 与(AND $\cdot$ ) 或(OR $+$ ) 非(NOT $\overline{X}$ )

反相圈

表示取反

拓展逻辑门¶

与非门(NAND $\overline{X\cdot Y}$ )
或非门(NOR $\overline{X + Y}$ )
异或门通常只能是二元运算(XOR $X \oplus Y = \overline{X}\cdot Y + \overline{Y}\cdot X$ ): 不一样的时候结果为1
同或门(NXOR $X \odot Y $) 异或门 + 非

数字抽象¶

0和1不表示数值的大小,而表示两种 相反的状态 如电平高低电路导通截止

在数字系统中, 将电压映射到两个状态(低L-未定义-高H)

四个临界电压

$V_{IHmin}$ input High min : 确保能被识别为高态的最小输入电压值
$V_{ILmin}$
$V_{OHmin}$ output High min : 输出为高态时的最小输出电压值
$V_{OLmin}$

Summary

输入可能因损耗导致电压变模糊, 因此输入的界限可以放宽, 但是输出还是要求尽可能标准.

CMOS晶体管---MOS¶

金属氧化物半导体场效应晶体管(三极晶体管)

栅极 gate
源极 source
漏极 drain

CMOS = NMOS + PMOS¶

complementary metal-oxide semiconductor

NMOS(negative) $\phi_s = 0V, \phi_g \ge 0, V_{gs} \ge 0$

栅极和源极电压 $V_{gs}$ 控制源极和漏极间电阻 $R_{ds}$ 的大小

$V_{gs} = \phi_g - \phi_s$

$V_{gs}$ 增大->导通->drain = source

PMOS(positive) $\phi_s = V_{DD} \approx 5.0V, V_{gs} \le 0$

$V_{gs}$ 降低->导通->drain = source

NMOS vs. PMOS

图形符号:PMOS带反相圈
$\phi_g$ 低-> $V_{gs2}$ 低->导通 $V_{DD}$ -> $V_{out}$ 高
$\phi_g$ 高-> $V_{gs1}$ 高->导通 $V{GND}$ -> $V_{out}$ 低

CMOS实现与非门¶

NMOS串联: 需要两个均导通

PMOS并联: 有一个导通即可

导通条件:

CMOS实现或非门¶

NMOS并联:

PMOS串联:

为什么先实现与非门或非门?

最少对数的CMOS实现, 与门(3对) = 与非门(2对) + 非门(1对).

CMOS-k输入¶

将2变成k, 串联/并联不变.

级联¶

一般输入端数目 $\le$ 5个, 最多不超过8个.

分级连接->速度更快/体积更小

缓冲器¶

非门+非门 ==> 将一个"弱信号"转换为具有相同逻辑值的"高信号": 降低出错的概率.

传输门¶

信号(EN) 使能端

EN高: 低->NMOS->低, 高->PMOS->高 EN低: 关闭

CMOS电路电气特性^*¶

转换时间transition time 0-1转换时间
传播延迟propagation delay 输入变换引起输出变化的延迟
静态/动态损耗

第二讲布尔代数¶

逻辑函数: 表明输入和输出变量之间的关系

运算顺序

() > $\overline{X}$ > $\cdot$ > +

对偶定律¶

两个逻辑表达式相等, 则它们的对偶式也相等.

广义德摩根定理

$\overline{F(X_1,X_2,\cdots, X_n, \cdot, *)} = F(\overline{X_1}, \overline{X_2}, \cdots, \overline{X_n}, *, \cdot)$

香农定理

广义结合律的逆用

逻辑函数的标准表示¶

标准乘积项: 最小项

编号: 只有当输入为 $i$ 时, 输出为1, 记为 $m_i$ .

标准和/最小项列表: 使得函数输出为1的最小项之和.

标准求和项: 最大项

编号: 只有当输入为 $i$ 时, 输出为0, 记为 $M_i$ .

标准积/最大项列表: 使得函数输出为0的最大项之积.

两者互补.

$f(A, B, C ) = \sum m(0, 1, 2) = \prod M(3, 4, 5, 6, 7)$

卡诺图化简¶

每一行列的编号对应逻辑变量的输入组合
编号按照格雷码的顺序排列, 即相邻编号只有一位不同.
根据格雷码的规则, 空间位置上相邻的小方格具有逻辑相邻性.
行列可互换
在对应最小项在真值表中的输出值为1的方格上置1, 称之为"1单元".
找1相邻(必须是 $2^n$ 个才能画(卡诺)圈)->说明存在变量无论取0还是1都为真->变量无意义, 可消去.

蕴含项

质蕴含项(prime implicant) : 不能被逻辑函数的其他蕴含项所覆盖(cover)的蕴含项.

实质蕴含项(essential prime implicant) 覆盖的最小项中至少有一个最小项不能没其他之蕴含项所覆盖的质蕴含项.

essential之处在于只有该蕴含项能覆盖那(几)个最小项.

卡诺圈越大, 质蕴含项所覆盖的最小项越多, 越可能是实质蕴含项.

步骤

将 $F(A,B,C,D) = \sum m(i_1, i_2, \cdots i_n)$ 的形式转化为卡诺图
找质蕴含项
在质蕴含项中找实质蕴含项
未被实质蕴含项覆盖的部分用质蕴含项覆盖
转化为逻辑表达式形式

逻辑函数变换¶

利用德摩根定理, 通过 $x = \overline{\overline{x}}$ 的方式进行等价变换, 来提高实际传输效率.

任何积之和的形式, 可以转换为"与非-与非"的形式
任何和之积的形式, 可以转换为"或非-或非"的形式

第三章组合逻辑电路¶

概述¶

数字逻辑电路分为组合(combinational)和时序(sequential)两种类型

组合逻辑电路的输出值仅依赖于当前输入值
时序逻辑电路的输出值还与当前的状态有关^*

组合逻辑电路的构成规则

元件本身是组合逻辑电路
输出节点不能互连
输出节点不能反馈到输入端

逻辑电路图¶

扇入系数: 一个逻辑门所允许的输入端的最大数目
扇出系数: 一个逻辑门输出端信号所能驱动的下一级输入端的最大数目

优先级顺序: 非 > 与/与非 > 异或(同或) > 或/或非

注意: 形如 $\overline{\overline{A}\cdot B \cdot C \oplus C + A + D}$ 这样的逻辑表达式, 最外层的非需要和与(+)连起来看成与非!

两级和多级组合逻辑电路¶

门延迟(gate delay): 信号通过逻辑门时在时间上的延迟

任何逻辑表达式都可以转换成与_{或表达式和或}与表达式, 因此, 任何组合逻辑电路都是可以是一个两级电路.

好处是降低了门延迟, 坏处是所需的硬件数量会成倍增长.

怎么证明?

组合逻辑电路设计¶

三道门: 非门->与门->或门

关注门延迟: 信号在每一道门处同时到达.

无关项,非法值和高阻态¶

无关项: 对于某些未定义的输入, 其输出时无关紧要的, 这些输入组合对应的输出值在化简时可以标识为d, 可以规定输出值为0或1.

无关项的输出值的设定可以便于卡诺图的化简

非法值: 信号值不能被有效识别为高电平或低电平, 处于不确定状态.

高阻态Hi-Z: 输出处于非正常逻辑态的第三种电气态, 就像是电路断开一样.

三态门(three-state-gate) 一种重要的总线接口电路, 也称三态缓冲器, 其输出为0/1/高阻态.

作用: 多个三态输出连在一起输出总线

典型组合逻辑部件¶

译码器(decoder)¶

反映输入和输出编码之间的映射关系.

$n-2^n$ 译码器

输入: n位 + 使能端
输出: $2^n$ 位

所有的输出中, 至多只有一位输入为1.

类似string2int.

编码器(encoder)¶

优先权编码器¶

多路选择器¶

注意

当控制端不止1位, MUX多层次级联时, 每一层的控制端是哪一位/用来区分哪些输入需要注意.

多路分配器¶

信号输出的分发.

半加器(HA)¶

A, B ==> Cout, S

全加器(FA)¶

A, B, Cin ==> Cout, S

组合逻辑电路时序分析¶

传输延迟和最小延迟¶

下降沿延迟 $t_{pHL}$
上升沿延迟 $t_{pLH}$
传输延迟 $T_{pd}$ : 从输入端的变化开始到所有输出端得到最终稳定的信号所需的最长时间.
最小延迟 $T_{cd}$ : 从输入端`的变化开始到任何一个输出开始发生改变所需的最短时间.
关键路径: 一个组合逻辑电路在输入和输出之间经过的最长路径.

传输延迟就是关键路径上所有元件的传输延迟之和.

最小延迟就是最短路径上所有元件的最小延迟之和.

竞争冒险¶

竞争(race): 某个信号A经过两条及以上的路径作用到输出端, 由于各路径传输延迟不同, 而导致该输入信号对输入端产生先后不同的影响.
毛刺(glitch): 例子: $A + \overline{A}$

第四章时序逻辑电路¶

输出结果不仅取决于当前时刻的输入值, 而且取决于电路过去时刻的行为(当前状态, 现态, 旧状态), 同时, 产生的影响不仅是输出, 也可能对状态产生影响.

例: 电视机遥控器的音量控制.

基本概念¶

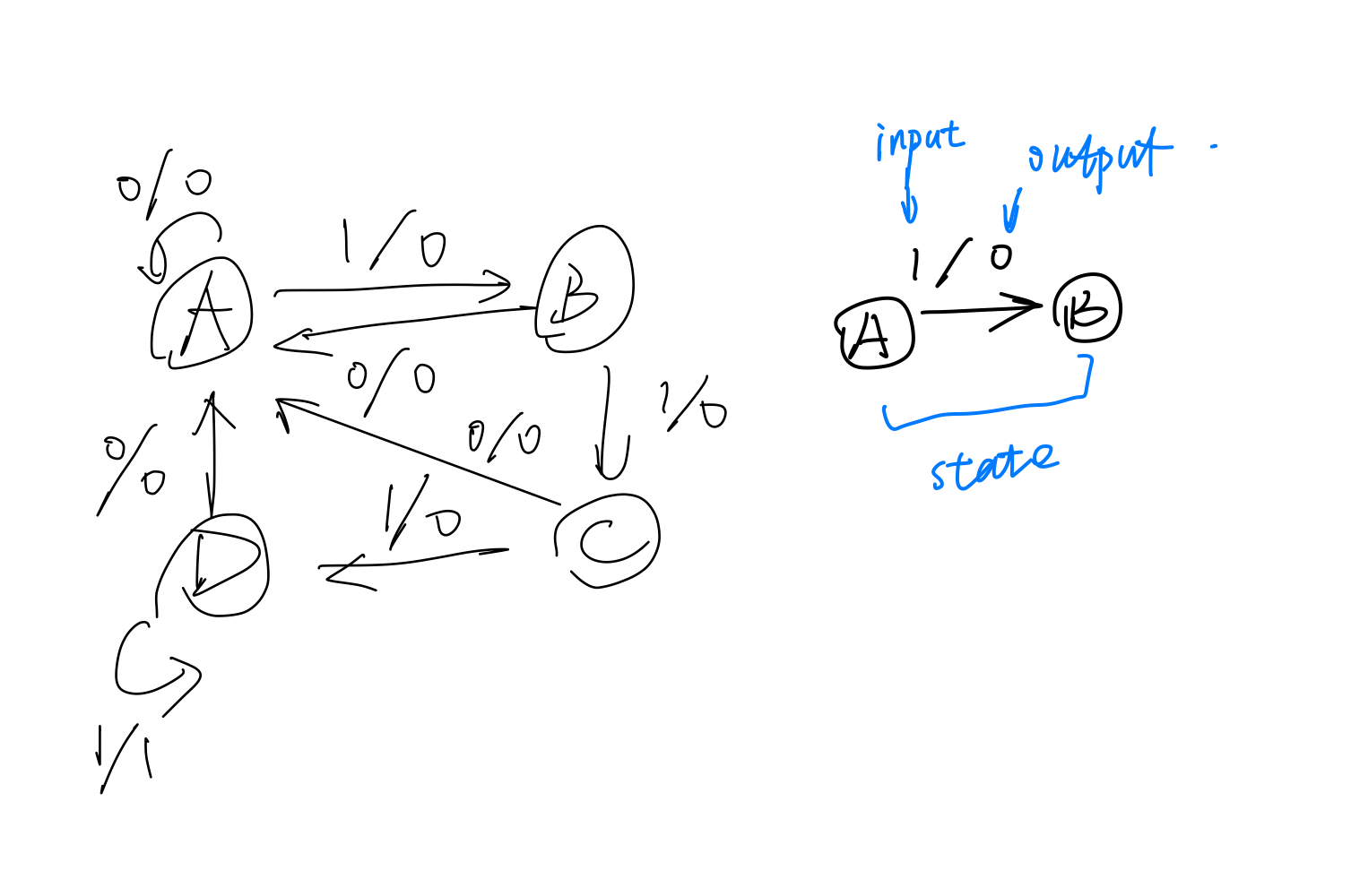
有限状态机(Finite State Machine, FSM)¶

一种刻画状态及状态转换的理论工具.

通常用状态图描述.

状态: 用包含状态符号的圆圈表示.
状态转换方向: 用有向边表示, 并在边上标注引起状态变化的输入信号值和相应输出.

状态的二进制编码: 把状态机的输入/输出以及内部状态都转换成二进制表示.

状态记忆电路(存储元件): 使用 双稳态记忆状态 , 如SR锁存器, D触发器, JK触发器等; 也可使用稳态电路记忆状态, 如反馈时序逻辑电路等.

激励函数: 根据当前输入把旧状态改为新状态的函数.

输出函数: 根据当前输入把旧状态改变电路的输出结果的函数.

定时分析

时序逻辑电路基本结构¶

[TODO] PPT 1.2(2页)

时钟脉冲

时钟信号(Clk): 按一定电压幅度, 按固定时间间隔, 连续发出的脉冲信号.

时钟脉冲之间的时间间隔为时钟周期 , 单位是秒.
通常1秒内产生的脉冲个数为时钟频率

锁存器和触发器¶

双稳态元件¶

状态1 置位状态(Set) 表示存储逻辑"1"
状态0 复位状态(Reset) 表示存储逻辑"0"

[TODO] 2.1PPT(2页)

锁存器latch[异步]¶

通过激励输入的电平信号来控制存储元件的状态.

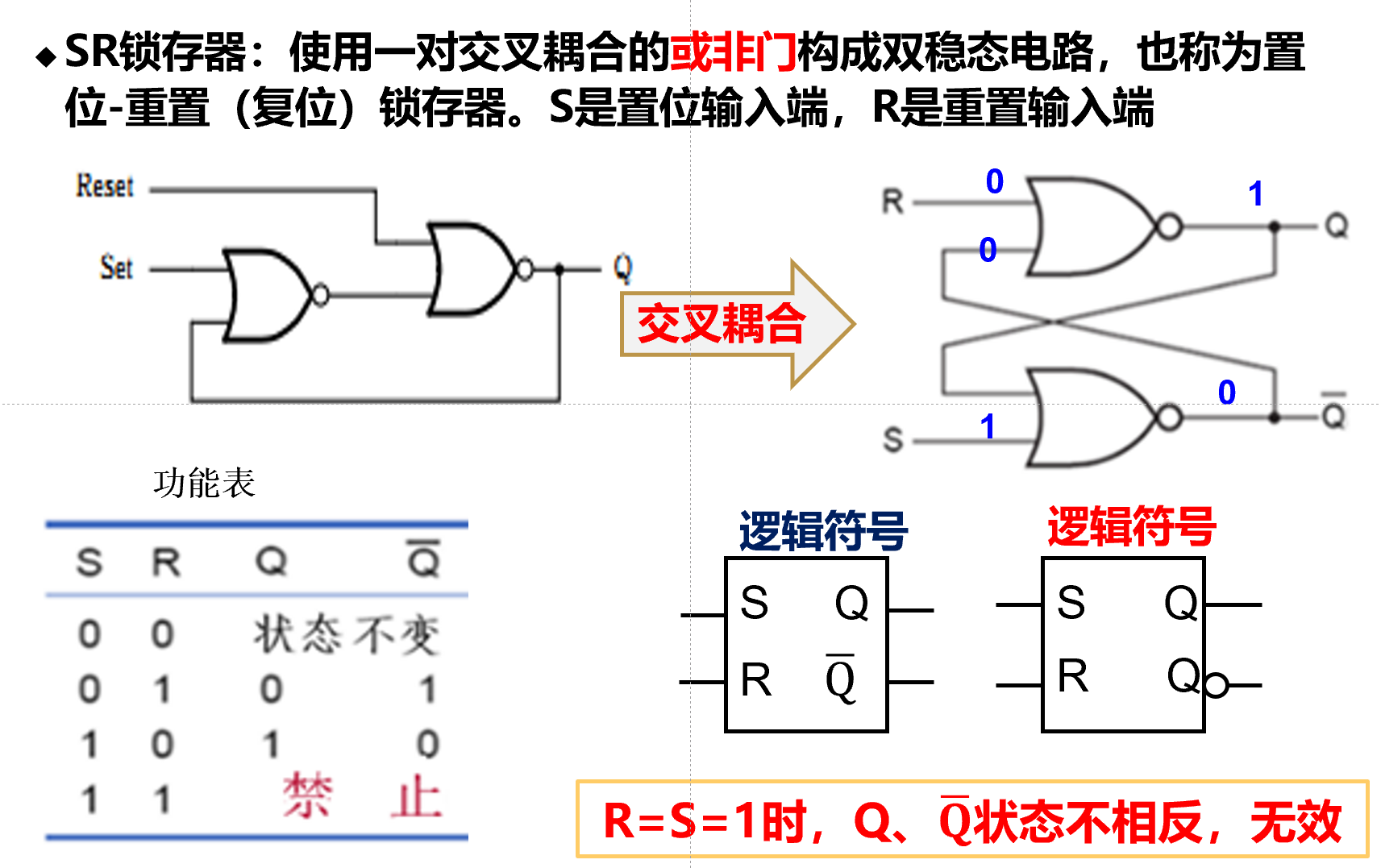
复位置位锁存器(Set-Reset latch)
- set有效->存储1
- reset有效->存储0
- 都无效->保持不变

触发器flip-flop[同步]¶

具有时钟控制信号作为存储转换的必要条件.

SR锁存器¶

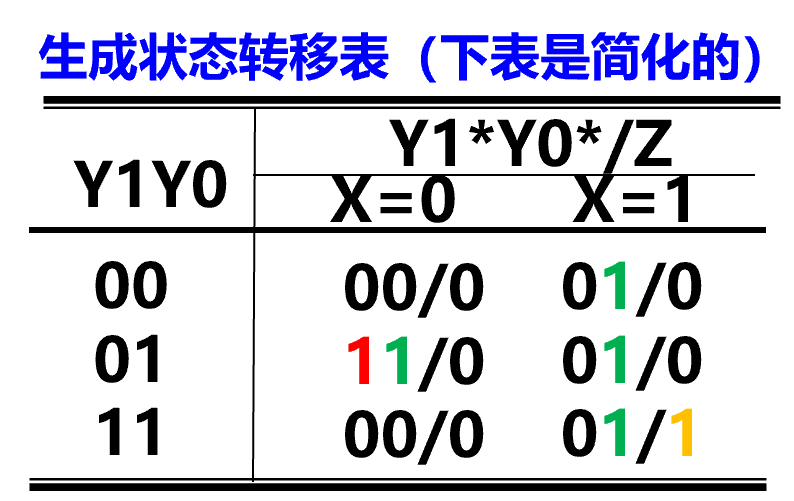
状态表

顶部为输入信号，左侧为现态Q
右侧填入次态Q*和输出信号

状态转移表

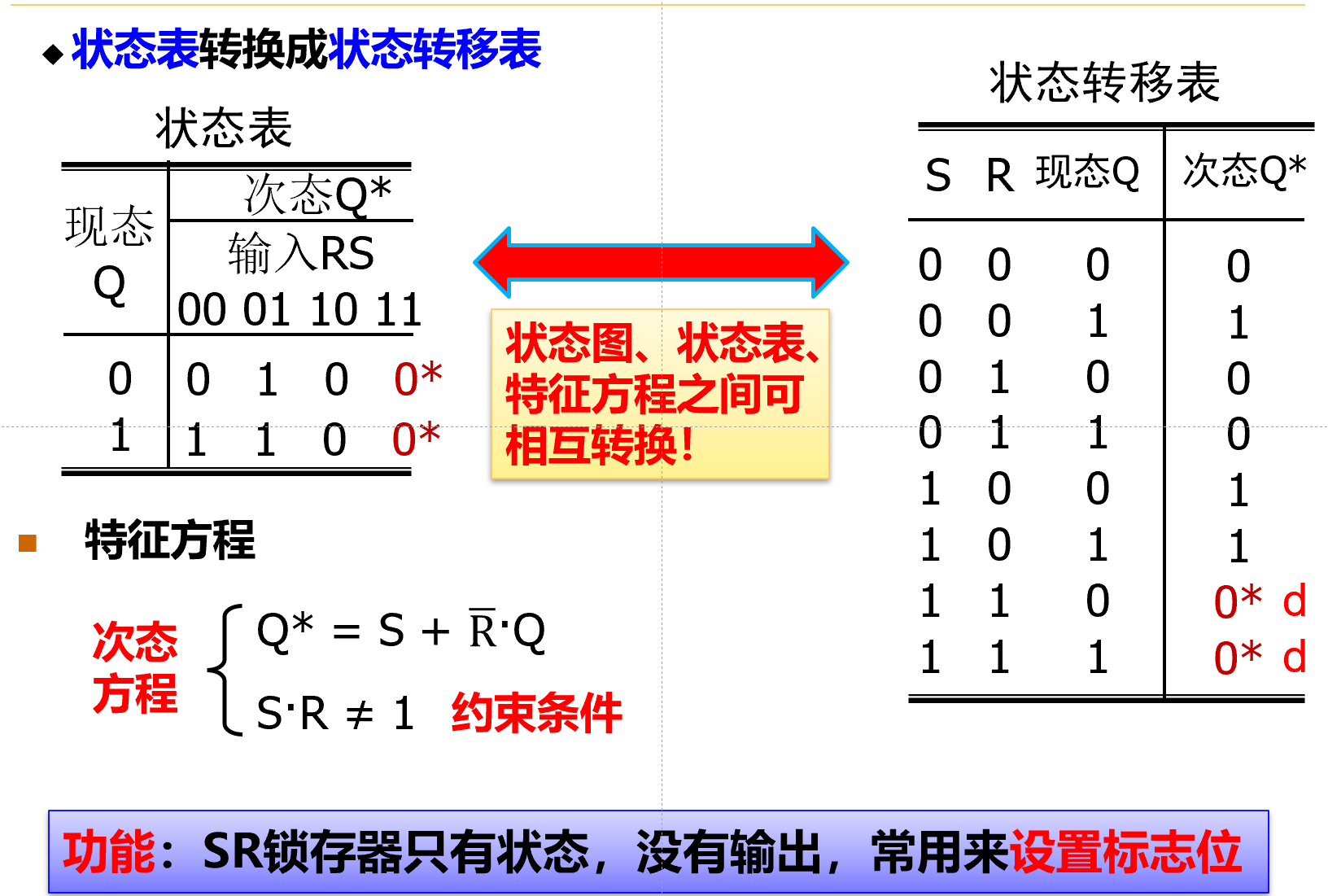
特征方程: 逻辑表达式, 化简过程类似卡诺图的化简. 可以通过自定义未定义状态(d)的真值来简化表达式.

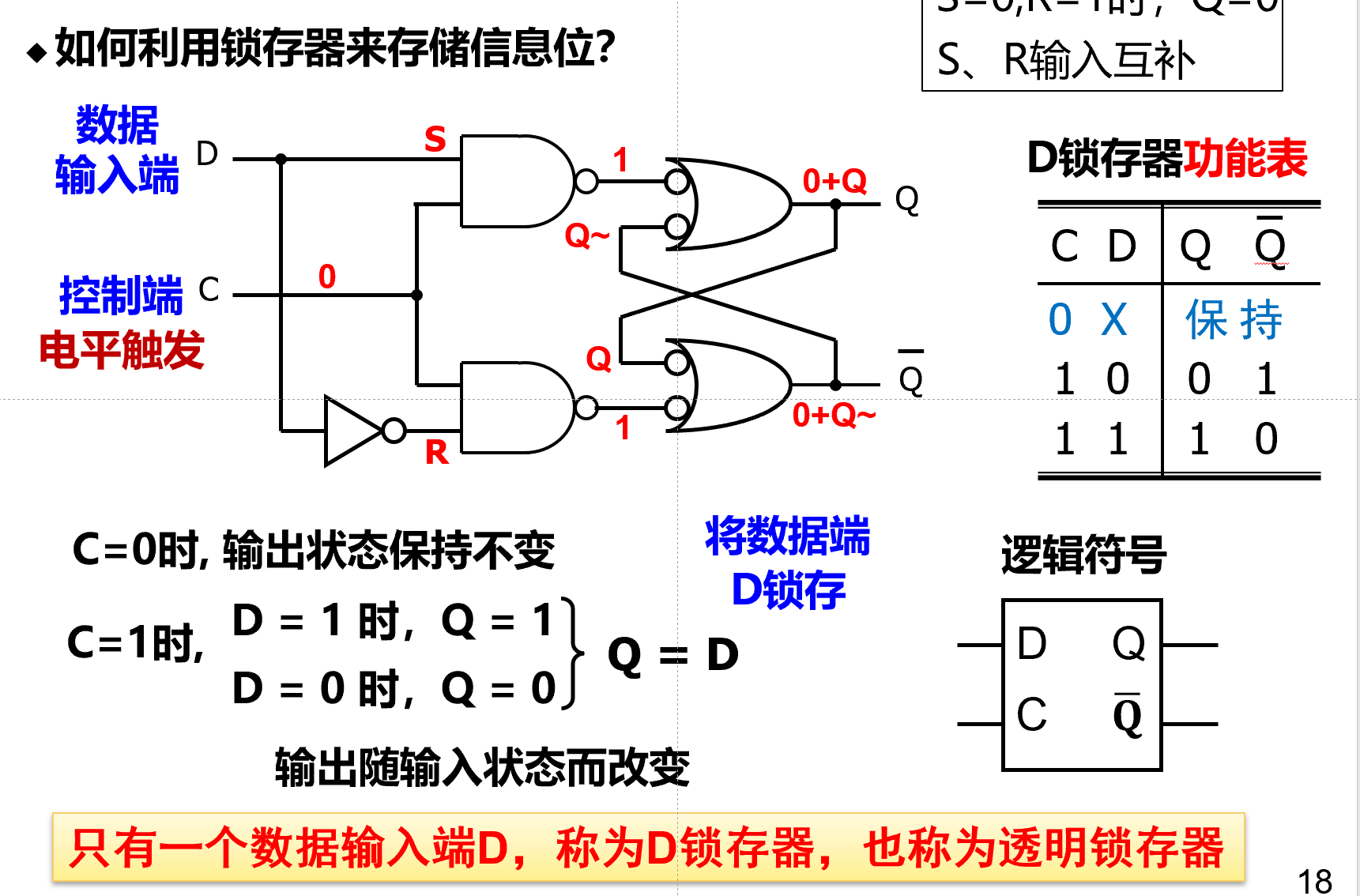
D锁存器¶

D触发器¶

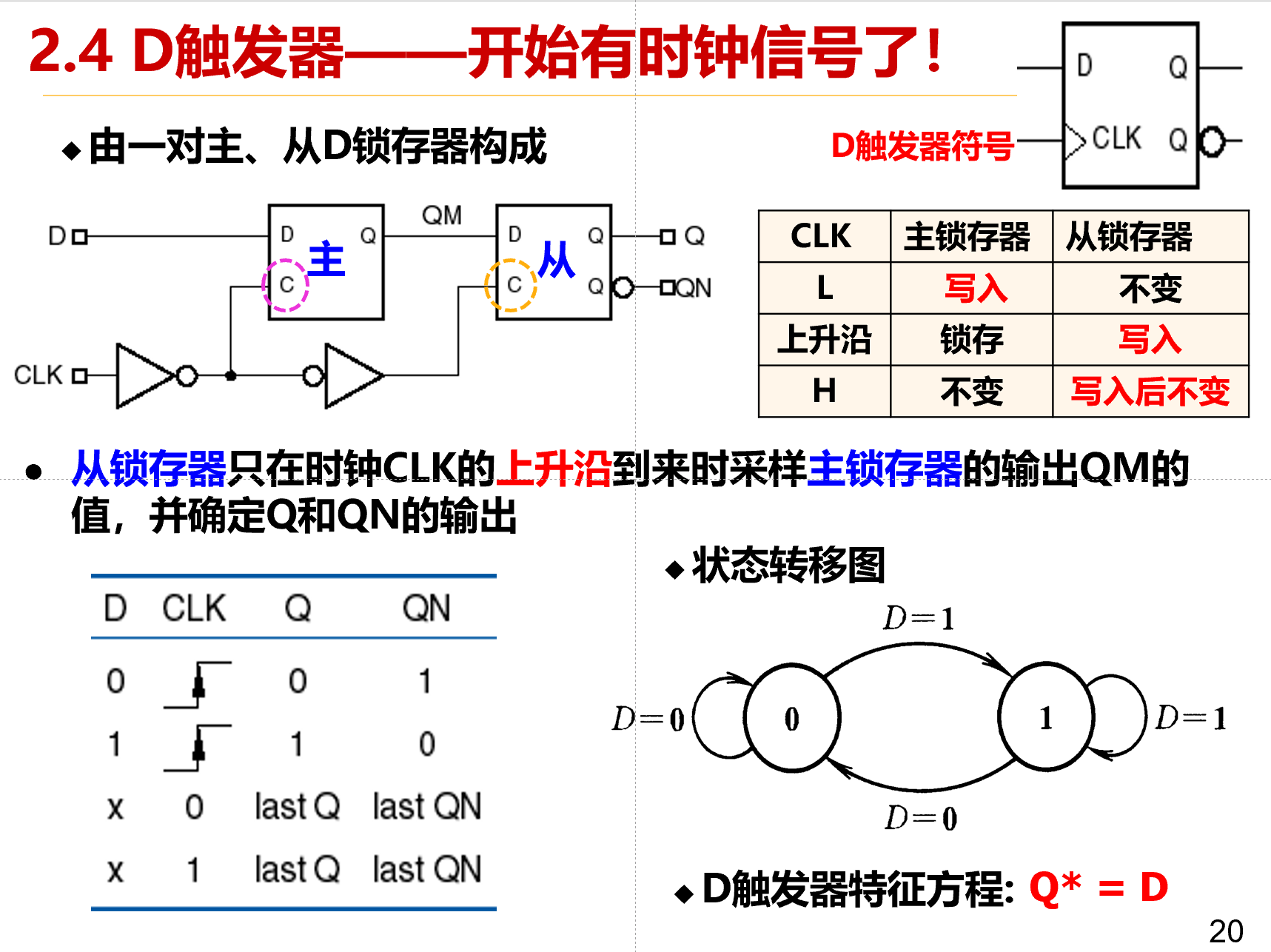
从时钟触发边沿到来,到输出端Q改变为D值的时间称为锁存延迟 $t_{CQ}$ (latch prop), 即CLK->Q时间，分 $t_{pLH(CQ)}$ 、 $t_{pHL(CQ)}$ 两种时间.

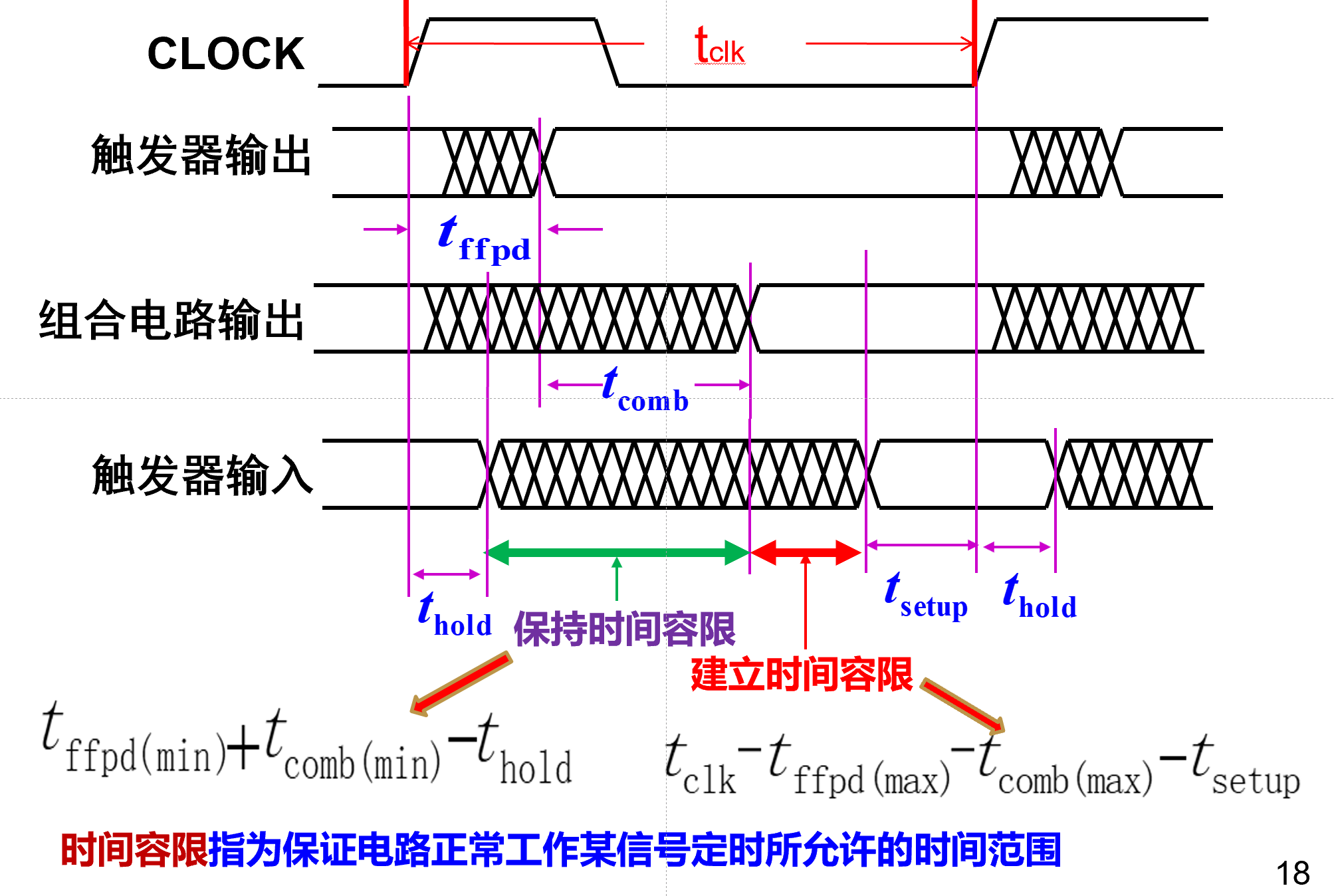
**保持时间容限

==> $t_{clk} > t_{ffpd(max)} + t_{comb(max)} + t_{setup}$

时钟周期不能太快, 但也不能太慢(效率低)时间** $t_{setup}$ ：输入信号D在时钟边沿到达前需稳定的时间

保持时间 $t_{hold}$ ：输入信号D在时钟边沿到达后需继续稳定的时间

这就意味着在clk的触发边沿到来前后, D值需要稳定.

带使能端的D触发器¶

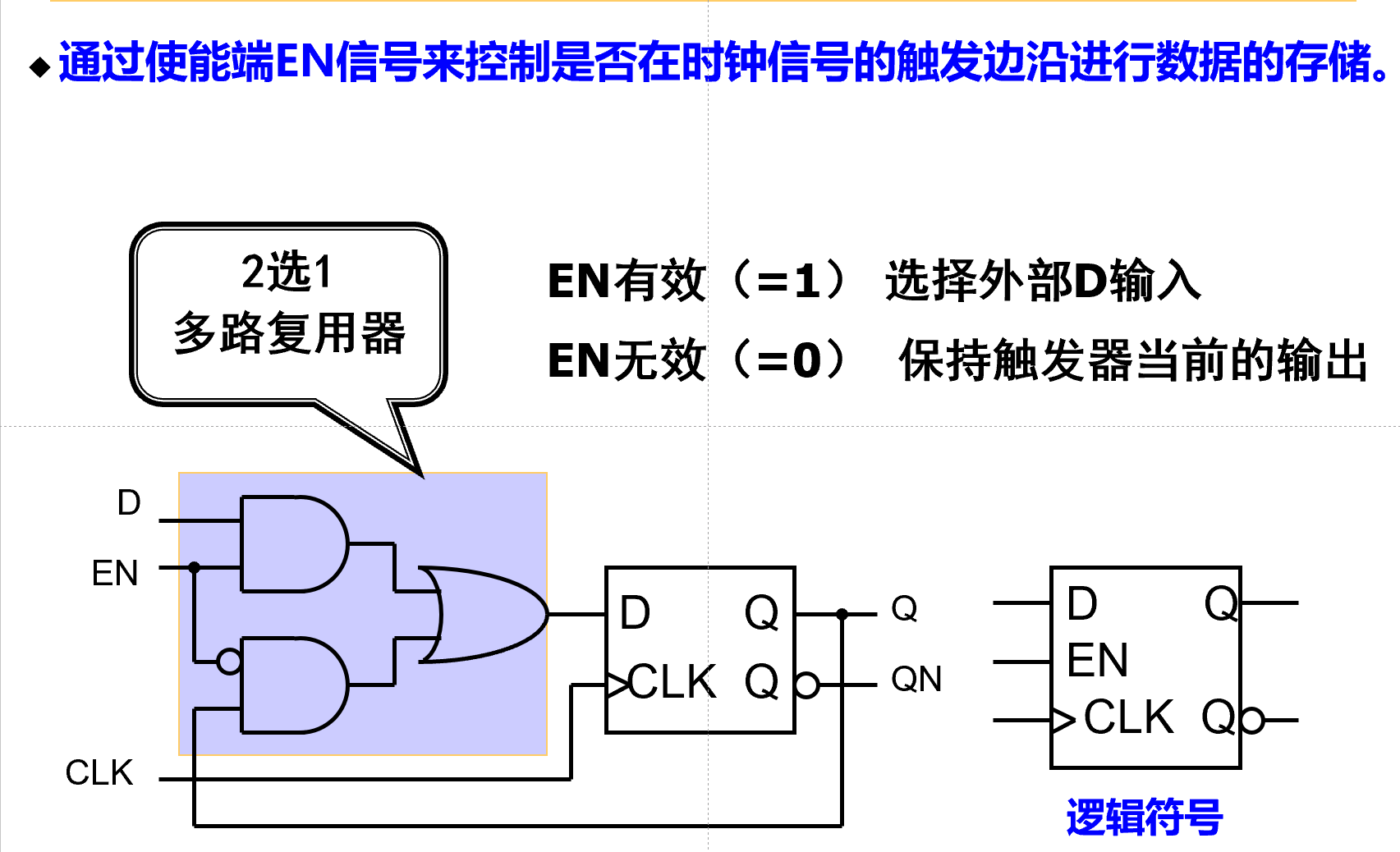
注意: 保持不变 和清零是两种不同的操作.

具有预制和清零(复位)端的D触发器¶

预制端PR(preset): 将Q置1
清零端CLR(clear): 将Q置0

T触发器¶

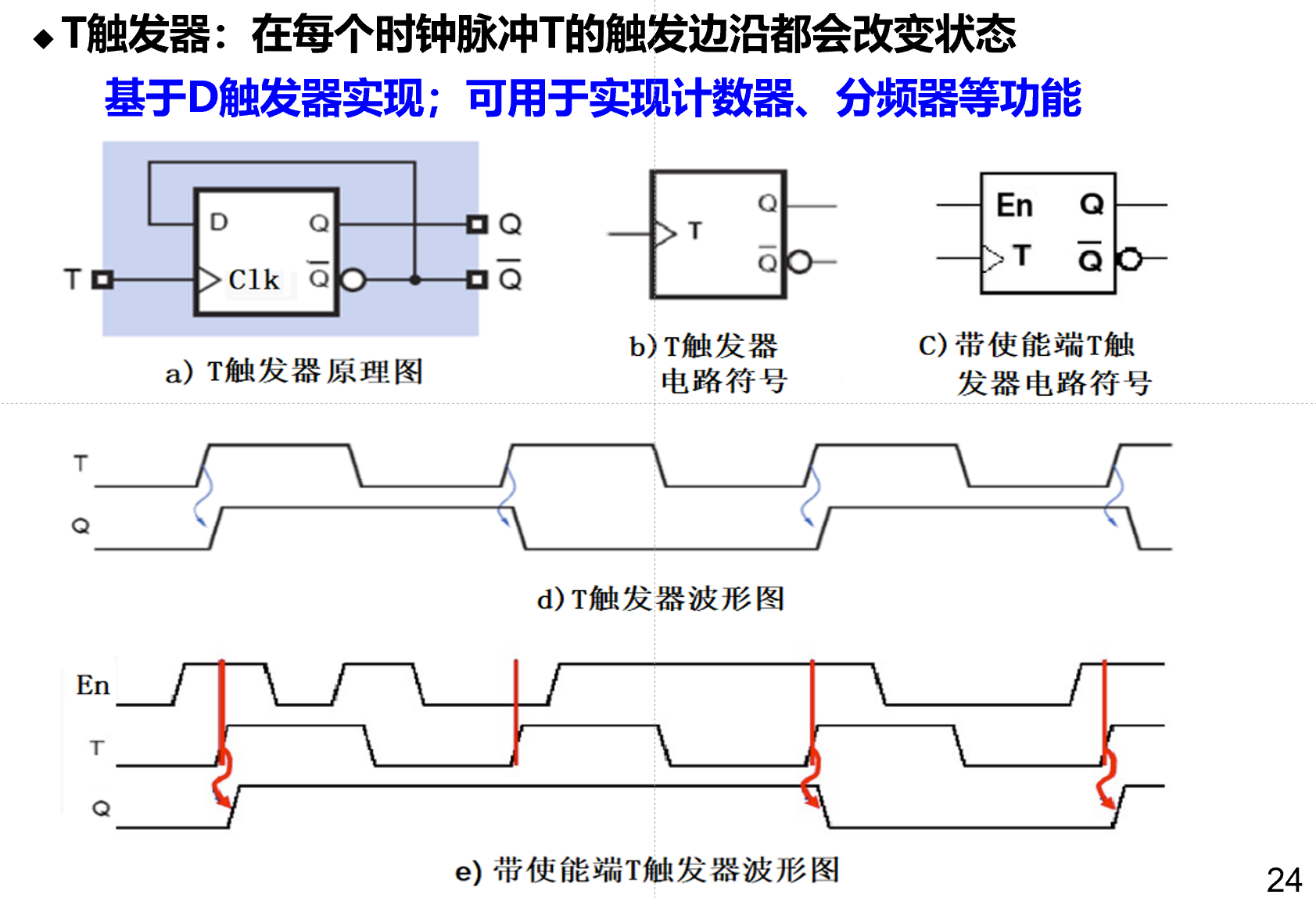
同步时序逻辑¶

需求分析¶

状态化简¶

合并等价状态.

等价状态

指在所有的输入组合下, 它们的输出和次态都相同或 次态等价 .

注意: 可能是递归地判定.

等价状态具有传递性.

状态编码¶

对状态表中每个状态赋予唯一的二进制编码, 也称状态赋值.
寻找最优编码方案是一个非常复杂的问题, 而不同的编码方案会产生不同的电路.
通常在具体设计中采用相邻法寻求次优编码方案.

相邻法

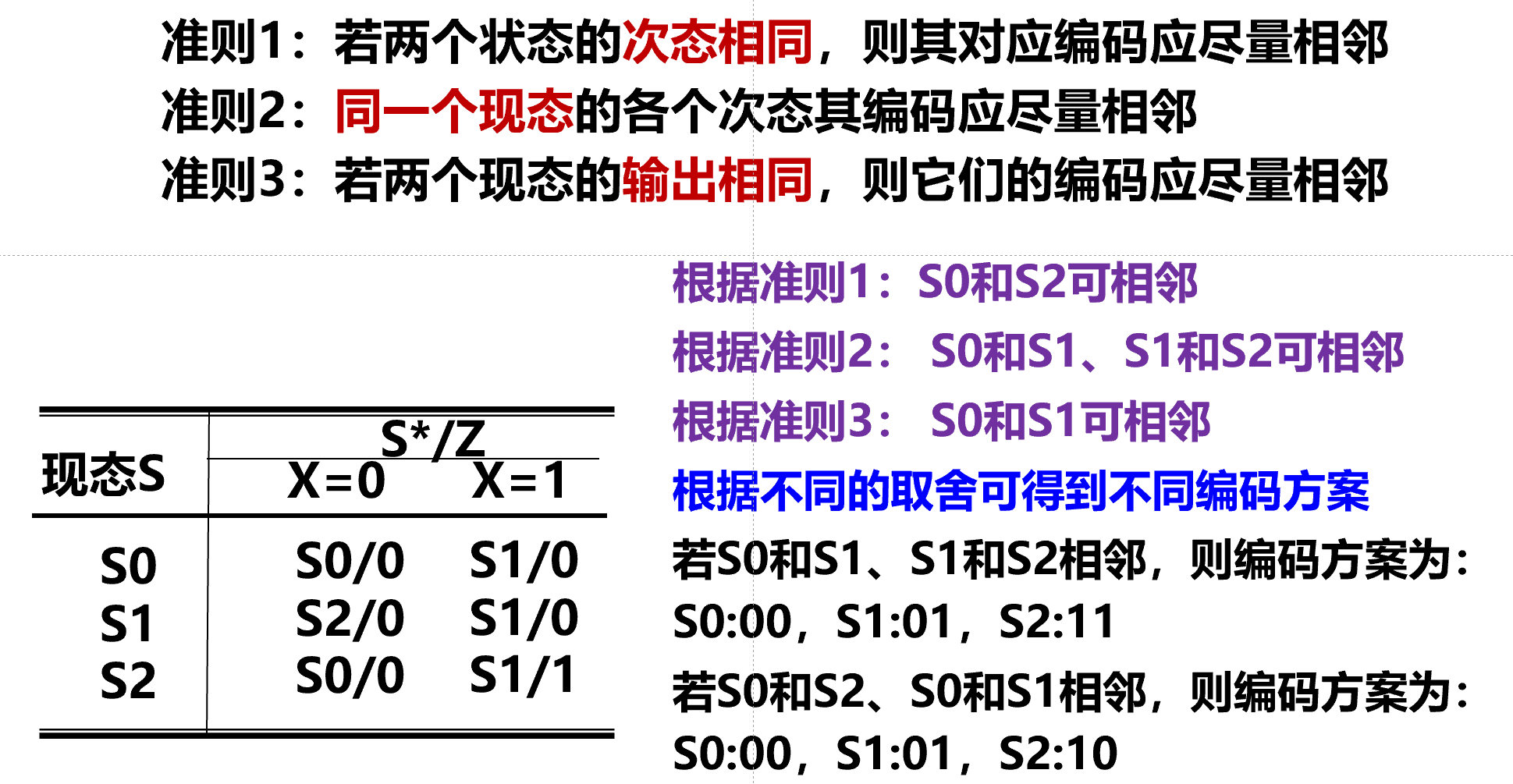
电路设计¶

未用状态分析¶

未用状态: 电路不需要, 也不会进入的状态.

在下图中, 状态10为未用状态.

挂起现象: 若电路进入未用状态, 且在未用状态之间循环转换而无法进入工作状态.

预置处理: 若触发器具有预置功能, 则可以通过预置处理, 是电路进入工作状态.

自启动: 判定电路进入未用状态能否在有限个时钟周期后进入工作状态. 若能, 且没有输出错误, 则称电路具有自启动.

定时分析¶

分析的重点在于次态的计算, 一般情况下, 输出不影响次态的计算, 只需要在下一个时钟周期到来前计算输出即可.

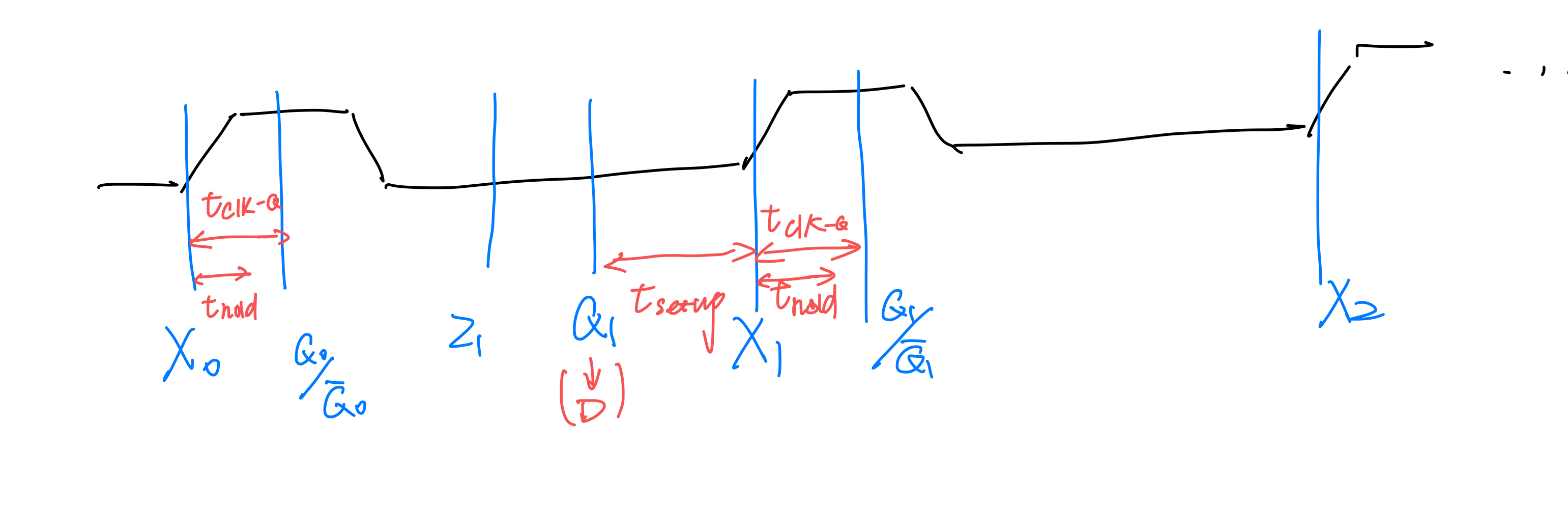
时间容限

建立时间容限
保持时间容限

==> $t_{clk} > t_{ffpd(max)} + t_{comb(max)} + t_{setup}$

时钟周期不能太快, 但也不能太慢(效率低)

典型时序逻辑部件设计¶

计数器¶

异步行波加法计数器
同步并行加法计数器
异步行波减法计数器

寄存器¶

写操作电路为时序逻辑电路, 读操作为组合逻辑电路.

移位寄存器¶

桶形移位器(无寄存功能)¶

第4章总结

第5章¶

第一讲可编程逻辑器件和FPGA设计¶

PLD分类¶

CPLD: 乘积项
FPGA: 查表法

PROM¶

与阵列固定或阵列可编程

PLA¶

与阵列或阵列都可编程

GAL¶

CPLD¶

存储器阵列¶

寄存器(由触发器构成)用来存储少量数据, 速度更快
存储器阵列用来存储大量的数据, 速度慢
ROM Read-Only Memory
RAM Random Access Memory

第六章运损方法和运算部件¶

第一讲基本运算部件¶

串行进位加法器¶

[TODO] PPT

并行进位加法器CLA¶

Carry look ahead 先行进位

[TODO] PPT 2页

n位带标志加法器¶

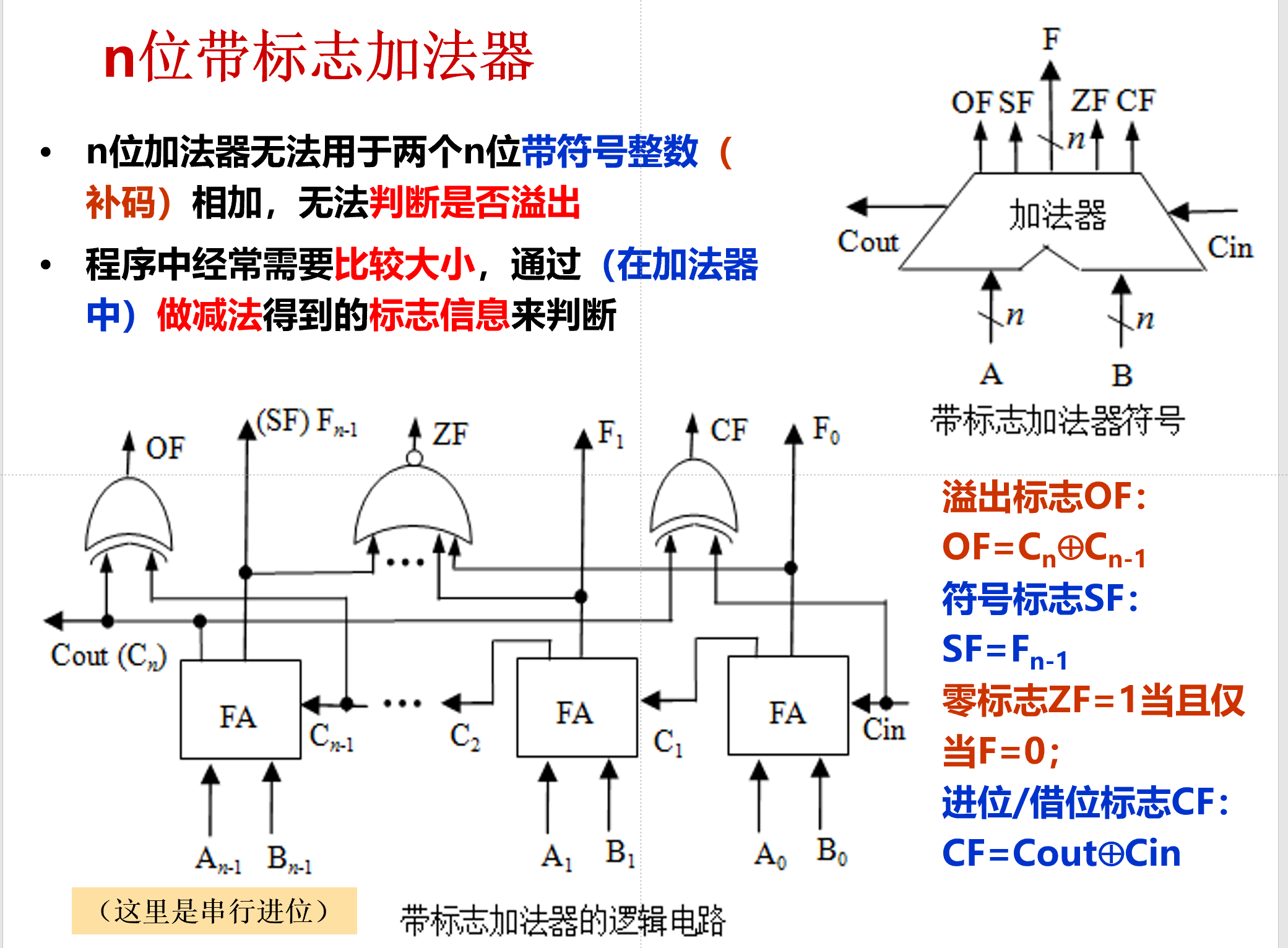
第二讲定点数运算¶

加减运算¶

n位整数加减运算器¶

除法运算¶

无符号数除法¶

恢复除法¶

不恢复余数除法¶

原理: (R - D + D) << 1 - D = (R-D) << R + D

第8章 CPU¶

数据通路的基本结构¶

由 操作元件 和 储存元件 通过总线或分线的方式.

状态元件: 分为寄存器(组)和理想存储元件.

数据通路与时序控制¶

同步系统(Synchronous system): 指令执行过程每一步都有控制信号控制, 由时序信号确定信号何时发出, 作用时间多长.

指令周期: CPU取并执行一条指令的时间, 不同指令的指令周期不一定相等.

计算机系统性能¶

Time to do the task
Tasks per sec

CPI: Cycles per Instruction

非总线式CPU¶

设计处理器的步骤

分析每条指令的功能, 并用RTL表示
根据指令的功能给出所需的元件
确定每个原价你所需控制信号的取值
汇总所有指令所涉及到的控制信号, 生成功能表
得到逻辑表达式, 构建 控制器 电路